自动搬运

查看原文

来自洛谷，原作者为

	hyfhaha AFO. 再见了，OI

搬运于2025-08-24 22:09:55，当前版本为作者最后更新于2019-05-10 13:42:09，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

因为是什么“二次加强版”，所以大家先去做一下“加强版”吧，做法差不多。

没做过的看这里:题解【模板】AC自动机（加强版），有一下变量名可能会在刚才那一篇blog出现过，所以建议大家再去过一下。

好了，看到这里大家都一定做过“加强版”了吧，那么这道题的做法也是差不多的，我们这一次不需要求出现最多的字符串啦，直接将vis数组输出就好了！（应该都知道vis数组是什么吧，就是统计每个模式串在文本串出现多少次的数组）

但重复的单词有没有影响啊！有啊！对于“加强版”，这一次重复的单词就会有影响啦，怎么办？

这道题有相同字符串要统计，设当前字符串是第i个，我们用一个Map[i]数组(不是STL那个)存((当前字符串在Trie中的那个位置)的flag)，最后把vis[Map[i]]输出就OK了。另外flag只在第一次赋值时变化，其他都不变。

代码中修改的地方：

插入字符串时insert：

insert最后那个地方,num是上面i的意思
if(!trie[u].flag)trie[u].flag=num;			//如果是第1个就赋值flag
Map[num]=trie[u].flag;									//存Map数组

最后输出：

for(int i=1;i<=n;++i)printf("%d\n",vis[Map[i]]);

嗯，没有问题了，交了！

？？？！怎么只有76分？TLE！！！ 提交记录

AC自动机的优化

拓扑建图优化

让我们来分析一下刚才那个程序的时间复杂度，算了不分析了，直接告诉你吧，这样暴力去跳fail的最坏时间复杂度是O(模式串长度 · 文本串长度)。为什么？因为对于每一次跳fail我们都只使深度减1，那样深度(深度最深是模式串长度)是多少，每一次跳的时间复杂度就是多少。那么还要乘上文本串长度，就几乎是 O(模式串长度 · 文本串长度)的了。

那么模板1的时间复杂度为什么就只有O(模式串总长)。因为每一个Trie上的点都只会经过一次（打了标记），但刚才那个程序每一个点就不止经过一次了，所以时间复杂度就爆炸了。

那么我们可不可以让刚才那个程序的Trie上每个点只经过一次呢？让时间复杂度降至O(模式串总长)呢？

嗯~，还真可以！

题目看这里：P5357 【模板】AC自动机（二次加强版）

做法：拓扑排序

让我们把Trie上的fail都想象成一条条有向边，那么我们如果在一个点使那个点进行一些操作，那么沿着这个点连出去的点也会进行操作（就是跳fail），所以我们才要暴力跳fail去更新之后的点。

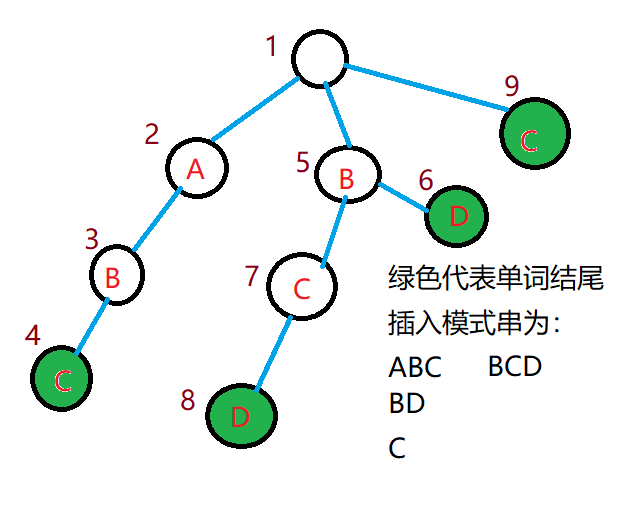
我们用上面的图，我举个例子解释一下我刚才的意思。

我们先找到了编号4这个点，编号4的fail连向编号7这个点，编号7的fail连向编号9这个点。那么我们要更新编号4这个点的值，同时也要更新编号7和编号9，这就是暴力跳fail的过程。

我们下一次找到编号7这个点，还要再次更新编号9，编号9点就被更新了两次，所以时间复杂度就在这里被浪费了。

那么我们可不可以在找到的点打一个标记，最后再一次性将标记全部上传 来 更新其他点的ans。例如我们找到编号4，在编号4这个点打一个ans标记为1，下一次找到了编号7，又在编号7这个点打一个ans标记为1，那么打好全部标记后，我们直接从编号4开始跳fail，然后将标记ans上传，((点i的fail)的ans)加上(点i的ans)，最后使编号4的ans为1，编号7的ans为2，编号9的ans为2，这样的答案和暴力跳fail是一样的，并且每一个点只经过了一次。

最后我们将有flag标记的ans传到vis数组里，就求出了答案。

但怎么确定更新顺序呢？明显我们打了标记后肯定是从深度大的点开始更新上去的。所以更新顺序就是从深度大的到深度小的。

怎么实现呢？拓扑排序！

我们使每一个点向它的fail指针连一条边，明显，每一个点的出度为1（fail只有一个），入度可能很多，所以我们就不需要像拓扑排序那样先建个图了，直接往fail指针跳就可以了。但入度数组in还是要存的。

最后我们根据fail指针建好图后（想象一下，程序里不用实现的），一定是一个DAG，具体原因不解释（很简单的），那么我们就直接在上面跑拓扑排序，然后更新ans就可以了。

代码实现：

首先是getfail这里，记得将fail的入度更新。

trie[v].fail=trie[Fail].son[i]; in[trie[v].fail]++;  	//记得加上入度

然后是query，不用暴力跳fail了，直接打上标记就行了，很简单吧

void query(char* s){
	int u=1,len=strlen(s);
	for(int i=0;i<len;++i)
	u=trie[u].son[s[i]-'a'],trie[u].ans++;							//直接打上标记
}

最后是拓扑，解释都在注释里了OwO!

void topu(){
	for(int i=1;i<=cnt;++i)
	if(in[i]==0)q.push(i);				//将入度为0的点全部压入队列里
	while(!q.empty()){
		int u=q.front();q.pop();vis[trie[u].flag]=trie[u].ans;	//如果有flag标记就更新vis数组
		int v=trie[u].fail;in[v]--;		//将唯一连出去的出边fail的入度减去（拓扑排序的操作）
		trie[v].ans+=trie[u].ans;		//更新fail的ans值
		if(in[v]==0)q.push(v);			//拓扑排序常规操作
	}
}

应该还是很好理解的吧，实现起来也没有多难嘛！

总代码

#include<bits/stdc++.h>
#define maxn 2000001
using namespace std;
char s[maxn],T[maxn];
int n,cnt,vis[200051],ans,in[maxn],Map[maxn];
struct kkk{
    int son[26],fail,flag,ans;
    void clear(){memset(son,0,sizeof(son)),fail=flag=ans=0;}
}trie[maxn];
queue<int>q;
void insert(char* s,int num){
    int u=1,len=strlen(s);
    for(int i=0;i<len;i++){
        int v=s[i]-'a';
        if(!trie[u].son[v])trie[u].son[v]=++cnt;
        u=trie[u].son[v];
    }
    if(!trie[u].flag)trie[u].flag=num;
    Map[num]=trie[u].flag;
}
void getFail(){
    for(int i=0;i<26;i++)trie[0].son[i]=1;
    q.push(1);
    while(!q.empty()){
        int u=q.front();q.pop();
        int Fail=trie[u].fail;
        for(int i=0;i<26;i++){
            int v=trie[u].son[i];
            if(!v){trie[u].son[i]=trie[Fail].son[i];continue;}
            trie[v].fail=trie[Fail].son[i]; in[trie[v].fail]++;
            q.push(v);
        }
    }
}
void topu(){
    for(int i=1;i<=cnt;i++)
    if(in[i]==0)q.push(i);
    while(!q.empty()){
        int u=q.front();q.pop();vis[trie[u].flag]=trie[u].ans;
        int v=trie[u].fail;in[v]--;
        trie[v].ans+=trie[u].ans;
        if(in[v]==0)q.push(v);
    }
}
void query(char* s){
    int u=1,len=strlen(s);
    for(int i=0;i<len;i++)
    u=trie[u].son[s[i]-'a'],trie[u].ans++;
}
int main(){
    scanf("%d",&n); cnt=1;
    for(int i=1;i<=n;i++){
        scanf("%s",s);
        insert(s,i);
    }getFail();scanf("%s",T);
    query(T);topu();
    for(int i=1;i<=n;i++)printf("%d\n",vis[Map[i]]);
}

如有需要，请看个人完整blog：AC自动机