1 条题解
-
0
自动搬运
来自洛谷,原作者为

Sooke
做被自己雪藏的耳廓狐 | https://codeforces.com/profile/Sulfox搬运于
2025-08-24 22:09:36,当前版本为作者最后更新于2019-05-01 23:08:57,作者可能在搬运后再次修改,您可在原文处查看最新版自动搬运只会搬运当前题目点赞数最高的题解,您可前往洛谷题解查看更多
以下是正文
前言
先来扯些真实的废话。
这八成是考场上最可做的题,原因有以下:
-
众所周知,数据范围越不正常的题越毒瘤,本题的数据范围就很正常。
-
往年省选包括今年 round 1 最简单的题中往往都有线段树,本题感性上就离不开线段树。
-
九条在出完 2、3、1 的开题顺序之后,喜欢出 2、1、3 的开题顺序。
遗憾的是,由于 round 1 的爆炸,考场上心态有点崩,智商骤降为 0,导致没做出此题。
可能我永远属于入场思维受阻、出场茅塞顿开的那种人吧。
解题思路
不难想到各种 的乱搞做法,比如链剖套扫描线 ,
听说会被九条定向卡。实际上有一种巧妙的 清真做法。若城市 能开展贸易,我们称 “ 可以到达 ”。
首先容易发现以下性质:
能到达的所有点恰好构成一棵生成树(即一个连通块)。
考虑这个生成树是怎么来的?可以进一步得出:
如果路径 包含点 , 则是 的两个极远点。
的生成树则是连通所有 的极远点的最小生成树。
举个例子,假设有三条路径分别是 , , 。
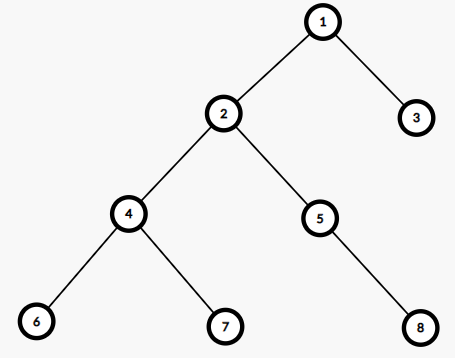
锁定 号点。路径 不经过它,对它没有任何贡献。其他路径则经过 号点,表明其有 个极远点: 。故生成树由 构成,即 号点能到达其他 个不同的点。
于是,我们需要事先思考子问题:给定树上若干的点,如何求最小生成树大小?
这应该是个经典问题。可能要用到一点建虚树的思想。
为了方便,我们硬点存在极远点 ,最后再计算其影响。
我们给这些点按照 序排序,然后一个一个地加进去。假设当前加入 号点,之前加入的点构成点集 , 的最小生成树是 。显然,为了使 和 连通,只需要找到 中离 最近的点连起来就好了,这“最近的点”正是 中的某个点与 的 。如果你对 序有较好的感觉,其实所谓 中的某个点,就是上一个加进去的点 !所以 的贡献是 $\mathrm{dep}_u - \mathrm{dep}_{\mathrm{lca}(u,\,v)}$ 。别忘了硬点了 号点,最后还要减 。
上面那段可能有点绕,强烈建议画个图感受一下!
暴力加点似乎不容易被利用,此时最擅长分治的线段树终于重磅登场了。
仍然是以 序为下标,线段树的叶子结点控制原树上每个点选或不选,每个结点表示了硬点 后一段区间的点集的最小生成树大小,并存下每个点集中下标最小和最大的点。类似地, 时要减去 。此时的 当然是左孩子已选下标最大的, 当然是右孩子已选下标最小的。查询的话只要用根结点的答案减去 即可。
白白套一个线段树不是多 吗?别急,正解已经浮出水面了。
想象每个结点都有一棵线段树。注意到有一条路径 ,我们会给该路径上的每棵线段树都选上 两点。按照套路,求出 ,等同于 两条链上执行线段树修改。仍然是套路,链上修改可以转换成树上差分打标记, 分别打上 。
慢着……线段树打标记是可以,但每个结点要把自己的信息继承给父亲,这怎么做?
动态开点 + 线段树合并!
至此,[ZJOI2019]语言 的大致做法讲完了。 次线段树合并是 的,而 次修改要求 次 ,如果树剖或倍增,复杂度是 ,如果使用欧拉序 表,复杂度是优美的 。
代码实现
刚才求的 没有强制 ,答案要除以 。
#include <cmath> #include <cstdio> #include <vector> #include <algorithm> const int N = 200005, V = 6400005, L = 18; int n, m, tms, o[N], ft[N], dep[N], dfn[N], st[L][N]; std::vector<int> to[N], del[N]; long long ans; inline int getLca(int u, int v); struct SegmentTree { int tot, c[V], f[V], s[V], t[V], ls[V], rs[V], rt[N]; inline void pushUp(int u) { f[u] = f[ls[u]] + f[rs[u]] - dep[getLca(t[ls[u]], s[rs[u]])]; s[u] = s[ls[u]] ? s[ls[u]] : s[rs[u]]; t[u] = t[rs[u]] ? t[rs[u]] : t[ls[u]]; } inline int query(int u) { return f[u] - dep[getLca(s[u], t[u])]; } void modify(int &u, int l, int r, int p, int x) { if (!u) { u = ++tot; } if (l == r) { c[u] += x; f[u] = c[u] ? dep[p] : 0; s[u] = t[u] = c[u] ? p : 0; return; } int mid = l + r >> 1; if (dfn[p] <= mid) { modify(ls[u], l, mid, p, x); } else { modify(rs[u], mid + 1, r, p, x); } pushUp(u); } void merge(int &u, int v, int l, int r) { if (!u || !v) { u |= v; return; } if (l == r) { c[u] += c[v]; f[u] |= f[v]; s[u] |= s[v]; t[u] |= t[v]; return; } int mid = l + r >> 1; merge(ls[u], ls[v], l, mid); merge(rs[u], rs[v], mid + 1, r); pushUp(u); } } smt; void build() { for (int i = 1; i <= tms; i++) { o[i] = log(i) / log(2) + 1e-7; } for (int i = 1; i <= o[tms]; i++) { for (int j = 1, u, v; j + (1 << i) - 1 <= tms; j++) { u = st[i - 1][j]; v = st[i - 1][j + (1 << i - 1)]; st[i][j] = dep[u] < dep[v] ? u : v; } } } inline int getLca(int u, int v) { if (!u || !v) { return 0; } u = dfn[u]; v = dfn[v]; if (u > v) { std::swap(u, v); } int d = o[v - u + 1]; u = st[d][u]; v = st[d][v - (1 << d) + 1]; return dep[u] < dep[v] ? u : v; } void dfs(int u, int fa) { ft[u] = fa; dep[u] = dep[fa] + 1; st[0][++tms] = u; dfn[u] = tms; for (auto v : to[u]) { if (v != fa) { dfs(v, u); st[0][++tms] = u; } } } void solve(int u) { for (auto v : to[u]) { if (v != ft[u]) { solve(v); } } for (auto v : del[u]) { smt.modify(smt.rt[u], 1, tms, v, -1); } ans += smt.query(smt.rt[u]); smt.merge(smt.rt[ft[u]], smt.rt[u], 1, tms); } int main() { scanf("%d%d", &n, &m); for (int i = 2, u, v; i <= n; i++) { scanf("%d%d", &u, &v); to[u].push_back(v); to[v].push_back(u); } dfs(1, 0); build(); for (int u, v, lca; m; m--) { scanf("%d%d", &u, &v); lca = getLca(u, v); smt.modify(smt.rt[u], 1, tms, u, 1); smt.modify(smt.rt[u], 1, tms, v, 1); smt.modify(smt.rt[v], 1, tms, u, 1); smt.modify(smt.rt[v], 1, tms, v, 1); del[lca].push_back(u); del[ft[lca]].push_back(u); del[lca].push_back(v); del[ft[lca]].push_back(v); } solve(1); printf("%lld\n", ans >> 1); return 0; }
尾注
看完后您还可真别说这题简单,考场上这么多算法的选择,鬼知道偏偏碰上了这一种呢?
-
- 1
信息
- ID
- 4317
- 时间
- 3000ms
- 内存
- 500MiB
- 难度
- 7
- 标签
- 递交数
- 0
- 已通过
- 0
- 上传者
