1 条题解

  • 0
    @ 2025-8-24 22:09:31

    自动搬运

    查看原文

    来自洛谷，原作者为

    avatar Great_Influence
    **

    搬运于2025-08-24 22:09:31，当前版本为作者最后更新于2019-04-24 19:59:25，作者可能在搬运后再次修改，您可在原文处查看最新版

    自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

    以下是正文

    平衡树裸题。

    首先，我们将一条边拆成两条边:上和下(或者左和右)，然后分别都标上号。

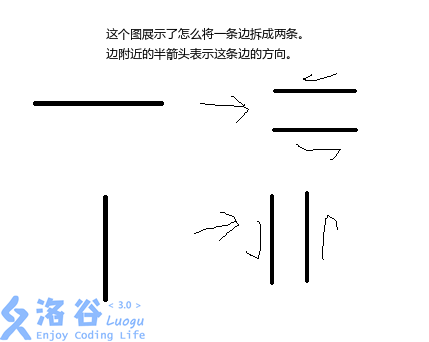
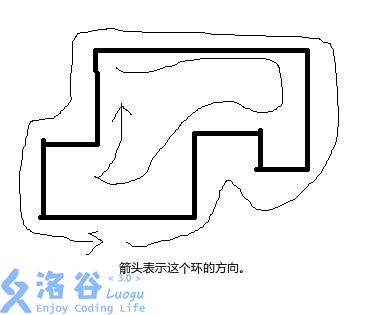
    然后，我们强制规定用左手摸着的前进方向为这条边的方向。对于一个闭合环的内圈，这个方向为顺时针，而对于外圈则是逆时针。

    可以借助示意图来辅助理解。

    因为我们没有什么东西能够很好地直接维护整个环，因此我们考虑拆掉环上的某条边。注意因为我们要求的是两条边之间的距离，因此我们给每条边建一个点，而原来的点不予维护。这里拆掉的边指的是边与边相交的边界。

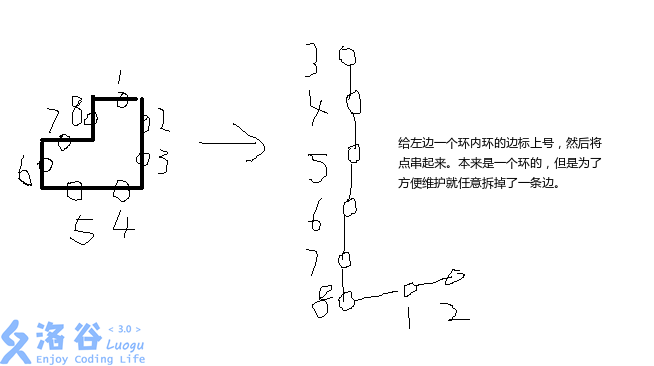
    可以发现，环上任意两相邻边代表点中间的边都可以拆掉。而具体拆掉的边我们可以快速更换，只需要将平衡树分裂成两部分，交换后重新合并即可。

    代码:

    inline void Cgbk(int u)
{
    int rk=order_of_key(u);//查询rank
    while(fa[u])u=fa[u];//找到根
    if(rk==sz[u])return;
    Pr y=split(u,rk);
    merge(y.second,y.first);
}

    然后，按照复杂程度开始讨论三个操作。

    1.询问

    我们可以将询问的边转成点，然后直接在平衡树上查询。

    如果这两个点属于同一棵平衡树，那么输出终点在平衡树上前面有多少个点减去起点前面有多少个点。因为拆的边可能会被经过，因此答案为负数时需要加上整棵平衡树的大小。

    否则直接输出 −1-1 。

    代码:

    read(x0),read(y0),read(x1),read(y1),read(d0);
read(x2),read(y2),read(x3),read(y3),read(d1);
if(x0+y0>x1+y1)swap(x0,x1),swap(y0,y1);
if(x2+y2>x3+y3)swap(x2,x3),swap(y2,y3);//先处理输入
int u=getid(x0<x1,x0,y0,d0),v=getid(x2<x3,x2,y2,d1);
if(getrt(u)^getrt(v)){write(-1);continue;}//无解
int z=order_of_key(v)-order_of_key(u);
if(z<0)z+=leafy_tree::sz[getrt(u)];
write(z);

    2.删除

    我们先查询删掉的边的两个半边是否在同一个环上。如果在，则删掉这条边只有可能将环分成两个(或者不变或者直接消失，但是可以一起考虑)。

    我们删掉后，平衡树序列会变成两部分，这两部分在环上都是连续的。

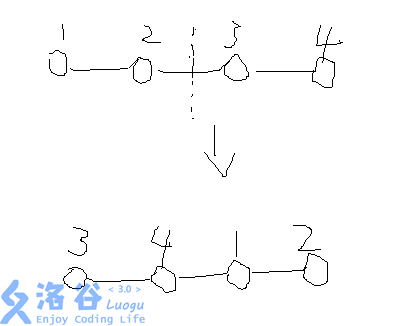
    因此，我们将删去边的其中一条更换到环的最后面，然后将平衡树在另一条的位置分裂成两部分。最后，我们将应该删去的两条半边删去即可。

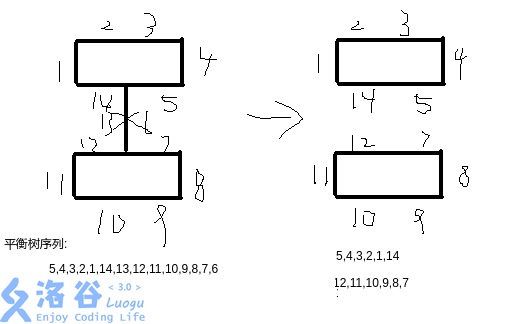
    如图。此次删掉的边为 6−136-13 这条边。

    否则如果不在一个环上的话，本次删除肯定会将这两个环合并成一个。

    因此，我们将删去的两个半边都调整到环的最后面，删掉这两个半边后直接将环首位相接即可。

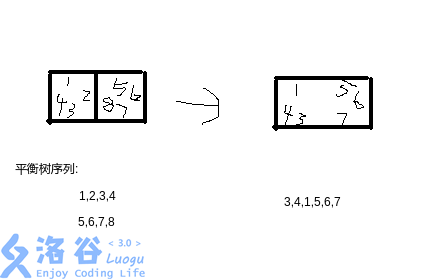
    如图，此次删掉的边为 2−82-8 这条边。

    代码:

    read(x0),read(y0),read(x1),read(y1);
if(x0+y0>x1+y1)swap(x0,x1),swap(y0,y1);//处理输入
hs[x0<x1][x0][y0]=0;//记得给每条存在的边打标记，在插入的时候要用
int u=getid(x0<x1,x0,y0,0),v=u+1;
if(getrt(u)==getrt(v))//在同一个环上
{
	Cgbk(v);
	int rt=split(getrt(u),order_of_key(u)-1).second;
	rt=split(rt,1).second;
	split(rt,leafy_tree::sz[rt]-1);
}
else//不在
{
	Cgbk(u),Cgbk(v);
	u=split(getrt(u),leafy_tree::sz[getrt(u)]-1).first,
	v=split(getrt(v),leafy_tree::sz[getrt(v)]-1).first;
	merge(u,v);
}

    3.插入

    最恶心的操作。

    我们考虑先求出来这样的两条边 ublubl 和 dbldbl ，分别表示两个半边插入后在环上的前一条边。

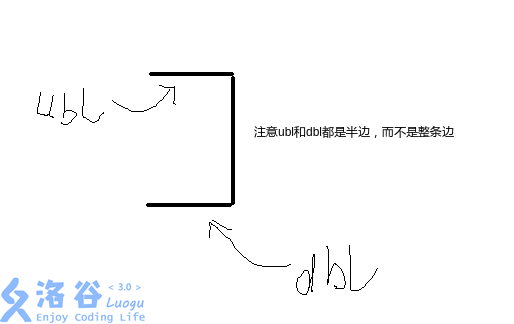
    如果两边都没有边的话，我们直接将两个半边首位相接。

    (这就不附图了)

    否则如果只有一边存在边，则直接将两个半边首位相接插入到那一边所在平衡树中。

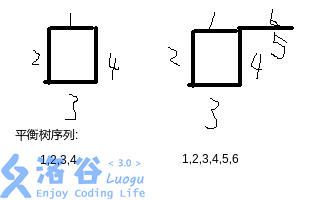
    否则我们查询 ublubl 和 dbldbl 是否在同一个环中。如果在的话，则这次插入会将原来的环拆成两个环。我们调整 ublubl 使它到这个环的最后面，然后将环在 dbldbl 的位置拆成两个部分，并在这两个部分的最后面分别插入两个半边。注意不能乱插。

    否则不在的话，这次插入会将两个环合并。我们调整 ublubl 和 dbldbl 变成环上最后一条边，分别接上两个半边后首位相接。注意半边的顺序。

    (最后两种情况可以直接看删边的图，倒过来就可以了)

    代码:

    inline void insert(int x0,int y0,int x1,int y1)
{
    int ubl=-1,dbl=-1;
    if(x0<x1)//先分情况找出ubl和dbl
    {
        if(y0&&hs[0][x0][y0-1])ubl=getid(0,x0,y0-1,1);
        else if(x0&&hs[1][x0-1][y0])ubl=getid(1,x0-1,y0,0);
        else if(hs[0][x0][y0])ubl=getid(0,x0,y0,0);

        if(hs[0][x1][y1])dbl=getid(0,x1,y1,0);
        else if(hs[1][x1][y1])dbl=getid(1,x1,y1,1);
        else if(y1&&hs[0][x1][y1-1])dbl=getid(0,x1,y1-1,1);
    }
    else
    {
        if(hs[1][x0][y0])ubl=getid(1,x0,y0,1);
        else if(y0&&hs[0][x0][y0-1])ubl=getid(0,x0,y0-1,1);
        else if(x0&&hs[1][x0-1][y0])ubl=getid(1,x0-1,y0,0);

        if(x0&&hs[1][x1-1][y1])dbl=getid(1,x1-1,y1,0);
        else if(hs[0][x1][y1])dbl=getid(0,x1,y1,0);
        else if(hs[1][x1][y1])dbl=getid(1,x1,y1,1);
    }
    if(~ubl&&~dbl)
    {
        if(getrt(ubl)==getrt(dbl))//在同一个环上的时候
        {
            Cgbk(ubl);
            Pr z=split(getrt(ubl),order_of_key(dbl));
            merge(z.second,getid(x0<x1,x0,y0,y0<y1));
            merge(z.first,getid(x0<x1,x0,y0,x0<x1));
        }
        else//不在同一个环上
        {
            Cgbk(ubl),Cgbk(dbl);
            merge(getrt(ubl),getid(x0<x1,x0,y0,y0<y1));
            merge(getrt(dbl),getid(x0<x1,x0,y0,x0<x1));
            merge(getrt(ubl),getrt(dbl));
        }
    }
    else
    {
        if(~ubl)Cgbk(ubl),merge(getrt(ubl)//只有一边有环
                ,merge(getid(x0<x1,x0,y0,y0<y1)
                    ,getid(x0<x1,x0,y0,x0<x1)));
        else if(~dbl)Cgbk(dbl),merge(getrt(dbl)
                ,merge(getid(x0<x1,x0,y0,x0<x1)
                    ,getid(x0<x1,x0,y0,y0<y1)));
        else merge(getid(x0<x1,x0,y0,0),getid(x0<x1,x0,y0,1));//两边都没有
    }
    hs[x0<x1][x0][y0]=1;//标记这条边出现过
}

    因为平衡树需要实现分裂合并，因此只能使用带有区间分裂能力的平衡树(如 splay,FHQ,splay,FHQ,leafy_tree) 。我这里写的是 leafy_tree 。

    总代码:

    #include<cstdio>
#include<cstdlib>
#include<cctype>
#include<cstring>
#include<algorithm>
#include<cmath>
#include<cassert>
#include<iostream>
#include<climits>
#define y1 djksaflsdajnfdsaknfkcjhdcfyduifbhrelfkcnrfr
#define Rep(i,a,b) for(register int i=(a);i<=(b);++i)
#define Repe(i,a,b) for(register int i=(a);i>=(b);--i)
#define rep(i,a,b) for(register int i=(a);i<(b);++i)
#define pb push_back
#define mp make_pair
#define mx(a,b) (a>b?a:b)
#define mn(a,b) (a<b?a:b)
typedef unsigned long long uint64;
typedef unsigned int uint32;
typedef long long ll;
using namespace std;

namespace IO
{
	const uint32 Buffsize=1<<15,Output=1<<24;
	static char Ch[Buffsize],*S=Ch,*T=Ch;
	inline char getc()
	{
		return((S==T)&&(T=(S=Ch)+fread(Ch,1,Buffsize,stdin),S==T)?0:*S++);
	}
	static char Out[Output],*nowps=Out;
	
	inline void flush(){fwrite(Out,1,nowps-Out,stdout);nowps=Out;}

	template<typename T>inline void read(T&x)
	{
		x=0;static char ch;T f=1;
		for(ch=getc();!isdigit(ch);ch=getc())if(ch=='-')f=-1;
		for(;isdigit(ch);ch=getc())x=x*10+(ch^48);
		x*=f;
	}

	template<typename T>inline void write(T x,char ch='\n')
	{
		if(!x)*nowps++='0';
		if(x<0)*nowps++='-',x=-x;
		static uint32 sta[111],tp;
		for(tp=0;x;x/=10)sta[++tp]=x%10;
		for(;tp;*nowps++=sta[tp--]^48);
		*nowps++=ch;
		if(nowps-Out>=1<<23)flush();
	}

	inline void getstr(char*q)
	{
		register char ch;
		for(ch=getc();!isgraph(ch);ch=getc());
		for(;isgraph(ch);ch=getc())*q++=ch;
		*q='\0';
	}

	inline void getwd(char&x){for(x=getc();!isupper(x);x=getc());}
}
using namespace IO;

void file()
{
#ifndef ONLINE_JUDGE
	FILE*DSD=freopen("water.in","r",stdin);
	FILE*CSC=freopen("water.out","w",stdout);
#endif
}

inline void Chkmin(int&u,int v){u>v?u=v:0;}

inline void Chkmax(int&u,int v){u<v?u=v:0;}

inline void Chkmax(double&u,double v){u<v?u=v:0;}

inline void Chkmax(ll&u,ll v){u<v?u=v:0;}

inline void Chkmin(ll&u,ll v){u>v?u=v:0;}

static int n,m,Q;

inline void init(){read(n),read(m),read(Q);}

const int MAXN=501,NODE=2e6+5e3;

inline int getid(int dr,int i,int j,int bk)
{
	if(!dr)return 2*(i*m+j+1)+bk-1;
	else return 2*(n+1)*m+2*(i*(m+1)+j+1)+bk-1;
}

static int lm;

typedef pair<int,int>Pr;

namespace leafy_tree
{
	const double alp=1-sqrt(2)/2;

	static int sz[NODE],son[NODE][2],fa[NODE];

	namespace Memery_Manage
	{
		static int sta[NODE],tp,cr;

		inline int newnode(){return !tp?++cr:sta[tp--];}

		inline void del(int u)
		{
			fa[son[u][0]]=fa[son[u][1]]=0;
			fa[u]=son[u][0]=son[u][1]=sz[u]=0;
			assert(u>lm);
			sta[++tp]=u;
		}
	}
	using Memery_Manage::newnode;
	using Memery_Manage::del;

	int build_tree(int*a,int l,int r)
	{
		if(l==r)return a[l];
		int md=(l+r)>>1,cr=newnode();sz[cr]=r-l+1;
		fa[son[cr][0]=build_tree(a,l,md)]
			=fa[son[cr][1]=build_tree(a,md+1,r)]=cr;
		return cr;
	}

	int merge(int u,int v)
	{
		if(!u||!v)return u|v;
		if(sz[u]>=sz[v]*alp&&sz[v]>=sz[u]*alp)
		{
			int cr=newnode();sz[cr]=sz[u]+sz[v];
			fa[son[cr][0]=u]=fa[son[cr][1]=v]=cr;
			return cr;
		}
		if(sz[u]>sz[v])
		{
			int ls=son[u][0],rs=son[u][1];del(u);
			if(sz[ls]>=alp*(sz[ls]+sz[rs]+sz[v]))return merge(ls,merge(rs,v));
			else
			{
				int lls=son[rs][0],rrs=son[rs][1];del(rs);
				return merge(merge(ls,lls),merge(rrs,v));
			}
		}
		else
		{
			int ls=son[v][0],rs=son[v][1];del(v);
			if(sz[rs]>=alp*(sz[u]+sz[ls]+sz[rs]))return merge(merge(u,ls),rs);
			else
			{
				int lls=son[ls][0],rrs=son[ls][1];del(ls);
				return merge(merge(u,lls),merge(rrs,rs));
			}
		}
	}

	Pr split(int u,int k)
	{
		if(!u||!k)return mp(0,u);
		if(k==sz[u])return mp(u,0);
		int ls=son[u][0],rs=son[u][1];del(u);
		if(sz[ls]>=k)
		{
			Pr y=split(ls,k);
			return mp(y.first,merge(y.second,rs));
		}
		else
		{
			Pr y=split(rs,k-sz[ls]);
			return mp(merge(ls,y.first),y.second);
		}
	}

	inline int order_of_key(int u)
	{
		register int sm=1;
		for(;fa[u];u=fa[u])if(u==son[fa[u]][1])
			sm+=sz[son[fa[u]][0]];
		return sm;
	}

	inline int getrt(int u){while(fa[u])u=fa[u];return u;}

	inline int Cgbk(int u)
	{
		int rk=order_of_key(u);
		while(fa[u])u=fa[u];
		if(rk==sz[u])return u;
		Pr y=split(u,rk);
		return merge(y.second,y.first);
	}

	void dfout(int u)
	{
		if(son[u][0])dfout(son[u][0]),dfout(son[u][1]);
		else cerr<<u<<' ';
	}
}
using leafy_tree::build_tree;
using leafy_tree::merge;
using leafy_tree::split;
using leafy_tree::order_of_key;
using leafy_tree::getrt;
using leafy_tree::Cgbk;
using leafy_tree::dfout;

static int hs[2][MAXN][MAXN];

inline void insert(int x0,int y0,int x1,int y1)
{
	int ubl=-1,dbl=-1;
	if(x0<x1)
	{
		if(y0&&hs[0][x0][y0-1])ubl=getid(0,x0,y0-1,1);
		else if(x0&&hs[1][x0-1][y0])ubl=getid(1,x0-1,y0,0);
		else if(hs[0][x0][y0])ubl=getid(0,x0,y0,0);

		if(hs[0][x1][y1])dbl=getid(0,x1,y1,0);
		else if(hs[1][x1][y1])dbl=getid(1,x1,y1,1);
		else if(y1&&hs[0][x1][y1-1])dbl=getid(0,x1,y1-1,1);
	}
	else
	{
		if(hs[1][x0][y0])ubl=getid(1,x0,y0,1);
		else if(y0&&hs[0][x0][y0-1])ubl=getid(0,x0,y0-1,1);
		else if(x0&&hs[1][x0-1][y0])ubl=getid(1,x0-1,y0,0);

		if(x0&&hs[1][x1-1][y1])dbl=getid(1,x1-1,y1,0);
		else if(hs[0][x1][y1])dbl=getid(0,x1,y1,0);
		else if(hs[1][x1][y1])dbl=getid(1,x1,y1,1);
	}
	if(~ubl&&~dbl)
	{
		if(getrt(ubl)==getrt(dbl))
		{
			Cgbk(ubl);
			Pr z=split(getrt(ubl),order_of_key(dbl));
			merge(z.second,getid(x0<x1,x0,y0,y0<y1));
			merge(z.first,getid(x0<x1,x0,y0,x0<x1));
		}
		else
		{
			Cgbk(ubl),Cgbk(dbl);
			merge(getrt(ubl),getid(x0<x1,x0,y0,y0<y1));
			merge(getrt(dbl),getid(x0<x1,x0,y0,x0<x1));
			merge(getrt(ubl),getrt(dbl));
		}
	}
	else
	{
		if(~ubl)Cgbk(ubl),merge(getrt(ubl)
				,merge(getid(x0<x1,x0,y0,y0<y1)
					,getid(x0<x1,x0,y0,x0<x1)));
		else if(~dbl)Cgbk(dbl),merge(getrt(dbl)
				,merge(getid(x0<x1,x0,y0,x0<x1)
					,getid(x0<x1,x0,y0,y0<y1)));
		else merge(getid(x0<x1,x0,y0,0),getid(x0<x1,x0,y0,1));
	}
	hs[x0<x1][x0][y0]=1;
}

static int a[NODE],z;

inline void solve()
{
	leafy_tree::Memery_Manage::cr=lm=2*(n*(m+1)+m*(n+1));
	Rep(i,1,lm)leafy_tree::sz[i]=1;
	Rep(i,0,m-1)a[++z]=getid(0,0,i,1),hs[0][0][i]=hs[0][n][i]=1;
	Rep(i,0,n-1)a[++z]=getid(1,i,m,0),hs[1][i][0]=hs[1][i][m]=1;
	Repe(i,m-1,0)a[++z]=getid(0,n,i,0);
	Repe(i,n-1,0)a[++z]=getid(1,i,0,1);
	build_tree(a,1,z),z=0;
	Repe(i,m-1,0)a[++z]=getid(0,0,i,0);
	Rep(i,0,n-1)a[++z]=getid(1,i,0,0);
	Repe(i,0,m-1)a[++z]=getid(0,n,i,1);
	Repe(i,n-1,0)a[++z]=getid(1,i,m,1);
	build_tree(a,1,z);
	static int op,x0,y0,x1,y1,x2,y2,x3,y3,d0,d1;
	Rep(i,1,n)Rep(j,1,m-1)
	{
		read(op);
		if(op)insert(i-1,j,i,j);
	}
	Rep(i,1,n-1)Rep(j,1,m)
	{
		read(op);
		if(op)insert(i,j-1,i,j);
	}
	while(Q--)
	{
		read(op);
		if(op==3)
		{
			read(x0),read(y0),read(x1),read(y1),read(d0);
			read(x2),read(y2),read(x3),read(y3),read(d1);
			if(x0+y0>x1+y1)swap(x0,x1),swap(y0,y1);
			if(x2+y2>x3+y3)swap(x2,x3),swap(y2,y3);
			int u=getid(x0<x1,x0,y0,d0),v=getid(x2<x3,x2,y2,d1);
			if(getrt(u)^getrt(v)){write(-1);continue;}
			int z=order_of_key(v)-order_of_key(u);
			if(z<0)z+=leafy_tree::sz[getrt(u)];
			write(z);
		}
		else
		{
			read(x0),read(y0),read(x1),read(y1);
			if(x0+y0>x1+y1)swap(x0,x1),swap(y0,y1);
			if(op==1)insert(x0,y0,x1,y1);
			else
			{
				hs[x0<x1][x0][y0]=0;
				int u=getid(x0<x1,x0,y0,0),v=u+1;
				if(getrt(u)==getrt(v))
				{
					Cgbk(v);
					int rt=split(getrt(u),order_of_key(u)-1).second;
					rt=split(rt,1).second;
					split(rt,leafy_tree::sz[rt]-1);
				}
				else
				{
					Cgbk(u),Cgbk(v);
					u=split(getrt(u),leafy_tree::sz[getrt(u)]-1).first,
					v=split(getrt(v),leafy_tree::sz[getrt(v)]-1).first;
					merge(u,v);
				}
			}
		}
	}
	flush();
}

int main()
{
	file();
	init();
	solve();
	return 0;
}
    • 1

    [BJOI2019] 送别

    信息

    ID
    4303
    时间
    2000ms
    内存
    500MiB
    难度
    7
    标签
    递交数
    0
    已通过
    0
    上传者
    1. 关于
    2. 联系我们
    3. 隐私
    4. 服务条款
    5. Language
    6. 主题
    3. Worker 0, 24ms