自动搬运

查看原文

来自洛谷，原作者为

	冒泡ioa **

搬运于2025-08-24 22:09:16，当前版本为作者最后更新于2019-04-16 19:34:05，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

更啰嗦的题解

题解

由于与运算和或运算在每一位上都是独立的，我们可以考虑对每一位进行计算。

我们先考虑与运算（其实两个运算是一样的）
于是就成了一个求一个矩阵中，有多少个0/1子矩阵，我们可以考虑用单调栈做。

有一个显然的结论

在一个 $N\times M$ 的矩阵中，以(n,m)为右下角的子矩阵共有 $N\times M$ 个

具体来讲，我们要求出一个s二维数组，s[i][j]表示(i,j)点上方有多少个连续的1，$O(N^2)$预处理

枚举每一个点，我们来计算以它为右下角的子矩阵个数 对于一般情况，在2处，A区域就没有意义，4处，B区域就没有意义 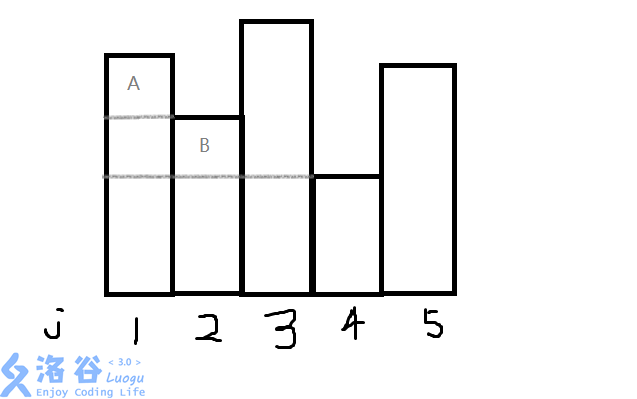所以我们要维护一个单调栈，栈中元素k要满足s[i][k]单调递增（栈顶s[i][k]最大）

每次有元素出栈时，说明有部分答案不能产生贡献，见代码注释

对于或运算，求所有0子矩阵，全集-0子矩阵数目即是贡献。

直接复制这个代码会T
ch上这样是过得了的，但是luogu上你需要加一个快读

代码

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int MAXN=2003,mod=1e9+7;
int ma[MAXN][MAXN];
int s[MAXN][MAXN];
int stk[MAXN],top;
int n;
ll ans1,ans2;

int main(){
	cin>>n;
	for(int i=1;i<=n;i++){
		for(int j=1;j<=n;j++){
			scanf("%d",&ma[i][j]);
		}
	}
	for(int k=0;k<31;k++){
		for(int i=1;i<=n;i++){
			for(int j=1;j<=n;j++){
				if((ma[i][j]>>k)&1)s[i][j]=s[i-1][j]+1;
				else s[i][j]=0;
			}
		}
		for(int i=1;i<=n;i++){
			ll ans=0;top=0;
			for(int j=1;j<=n;j++){
				ans+=s[i][j];
				while(top&&s[i][stk[top]]>=s[i][j]){
					ans-=(stk[top]-stk[top-1])*(s[i][stk[top]]-s[i][j]);
					//栈顶对于第二大的元素的距离×栈顶与j的落差，即为上图中j=3时灰色线的上半部分
					top--;
				}
				ans1+=ans<<k;
				ans1%=mod;
				stk[++top]=j;
			}
		}
	}
	cout<<ans1<<" ";
	for(int k=0;k<31;k++){
		for(int i=1;i<=n;i++){
			for(int j=1;j<=n;j++){
				if((ma[i][j]>>k)&1)s[i][j]=0;
				else s[i][j]=s[i-1][j]+1;
			}
		}
		for(int i=1;i<=n;i++){
			ll ans=0;top=0;
			for(int j=1;j<=n;j++){
				ans+=s[i][j];
				while(top&&s[i][stk[top]]>=s[i][j]){
					ans-=(stk[top]-stk[top-1])*(s[i][stk[top]]-s[i][j]);
					top--;
				}
				ans2+=(i*j-ans)<<k;
				ans2%=mod;
				stk[++top]=j;
			}
		}
	}
	cout<<ans2<<endl;
		
	return 0;
}