15011418730 LV 7 @ 2025-8-24 22:08:53

自动搬运

来自洛谷，原作者为

	ix35 垒球

搬运于2025-08-24 22:08:53，当前版本为作者最后更新于2022-09-08 15:32:40，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

NOI 2014 消除游戏

今天与这题大战半天，做之前没有在网上看到任何一篇这题的题解，做完之后才发现 UOJ 上有人写过博客，不过百度上也搜不到，所以我来写一下。

题目大意：

这是一道提交答案题。

给定 $n\times m$ 网格，网格中的数都是 $[0,9]$ 的整数。

每轮你可以选择一条简单路径，满足路径上每个格子都有数，且起始点的数不为 $0$ 。设你的路径长度为 $l$ ，路径上的数顺次构成一个整数 $X$ ：

如果 $X$ 是素数，则你的素数加分为 $l^{c_1}$ ，否则素数加分为 $1$ ；
如果 $X$ 是回文数，则你的回文加分为 $l^{c_2}$ ，否则回文加分为 $1$ 。

这轮操作的总分是素数加分和回文加分的和。但是特别地，如果 $X$ 既不是素数又不是回文数，则这个操作非法。

每轮操作结束后，路径上的所有数会消失，然后网格中所有数按重力规则下落。

你最多可以进行 $K$ 轮上述操作，并且每次的路径长度 $l$ 需要满足 $l_{min}\leq l\leq l_{max}$ 。

此外有一个参数 $F$ ，如果 $F=0$ ，则你的总分等于每轮操作总分之和；如果 $F=1$ ，则再设 $d$ 是操作结束后网格中剩下的数的个数，你的总分等于每轮操作的总分之和除以 $2^d$ 下取整。你要构造一个方案使得总分足够大（有一些不告诉你的评分参数）。

每个测试点给定的东西包括 $n,m,K,l_{min},l_{max},c_1,c_2,F$ 和初始的网格。

测试点 1：

$n=m=5,\ K=100,\ l_{min}=2,\ l_{max}=16,\ c_1=c_2=2,\ F=1$，网格如下：

我们发现右上角 $4\times 4$ 的块正好可以构成一个长度为 $16$ 的回文数 $1234567887654321$ ，而左下这一条是一个素数 $10^8+7$ 。

于是分成这两部分，可以通过该测试点。

测试点 2：

$n=m=10,\ K=100,\ l_{min}=2,\ l_{max}=8,\ c_1=c_2=1,\ F=1$，网格如下：

7 4 1 3 5 9 8 6 1 6
8 0 9 1 1 1 1 7 1 2
9 3 6 7 5 1 5 9 6 0
8 1 8 4 9 7 7 4 3 9
0 4 0 0 9 0 1 7 8 3
8 4 8 7 3 7 8 0 7 0
7 1 6 6 1 0 5 8 9 0
5 9 9 1 1 5 1 5 1 5
8 1 2 7 6 2 3 3 3 0
0 9 1 0 9 4 0 6 1 9

我们发现由于 $F=1$ ，所以关键在于要把所有数消除光。

可以写个暴力 DFS：每次随机一个起点，然后随机一条从它开始的简单路径，然后检验是否合法，如果合法就删除后递归。如果某个 DFS 分支已经走不下去了就回溯，只要记下之前的地图就可以轻易地完成回溯操作。

这个做法搜出的解大概可以得到 $[7,9]$ 分。

我们可以加个优化：只使用长度 $\leq 4$ 的路径，因为长度越小能蹭到的分数 $1$ 就越多，所以这样总分会稍微大一些，可以通过该测试点。

#include <bits/stdc++.h>
#define ll long long
#define ull unsigned long long
using namespace std;
const int N=110;
int n,m,k,l1,l2,c1,c2,f,mp[N][N],vis[N][N],dir[4][2]={{0,1},{0,-1},{1,0},{-1,0}};
vector < pair<int,int> > v; 
vector < vector < pair<int,int> > > ans; 
ull sd;
ull rd () {sd^=(sd<<27);sd^=(sd>>19);sd^=(sd<<25);return sd;}


ll qmul (ll a,ll b,ll p) {return (a*b-(ll)((long double)a/p*b)*p+p)%p;}
ll qpow (ll a,ll b,ll p) {
	ll res=1;
	while (b) {
		if (b&1) {res=qmul(res,a,p);}
		a=qmul(a,a,p),b>>=1;
	}
	return res;
}
bool mr (ll p,ll x) {
	if (qpow(x,p-1,p)!=1) {return 0;}
	ll k=p-1;
	while (!(k&1)) {
		k>>=1;
		ll tmp=qpow(x,k,p);
		if (tmp==p-1) {return 1;}
		else if (tmp!=1) {return 0;}
	}
	return 1;
}
bool isp (ll p) {
	if (p==46856248255981||p==1) {return 0;}
	if (p==2||p==3||p==7||p==61||p==24251) {return 1;}
	return mr(p,2)&&mr(p,3)&&mr(p,7)&&mr(p,61)&&mr(p,24251);
}


bool chk (int x,int y) {return (x>0&&y>0&&x<=n&&y<=m&&mp[x][y]!=-1&&!vis[x][y]);}
void sr () {
	int x=rd()%n+1,y=rd()%m+1,cc=0;
	while (mp[x][y]<=0&&cc<=200) {x=rd()%n+1,y=rd()%n+1,cc++;}
	if (mp[x][y]<=0) {return;}
	v.push_back(make_pair(x,y));vis[x][y]=1;
	for (int i=1;i<=4;i++) {
		int dr=rd()%4;
		for (int i=1;i<=4;i++) {
			if (!chk(x+dir[dr][0],y+dir[dr][1])) {dr=(dr+1)%4;}
		}
		if (!chk(x+dir[dr][0],y+dir[dr][1])) {break;}
		x+=dir[dr][0],y+=dir[dr][1];
		v.push_back(make_pair(x,y));vis[x][y]=1;
	}
	for (auto x:v) vis[x.first][x.second]=0;
}
bool chkk () {
	ll tmp=0;
	if (v.size()<=1) {return 0;}
	for (auto x:v) {tmp=tmp*10+mp[x.first][x.second];}
	int flg=1,len=v.size();
	for (int i=0;i<len;i++) {if (mp[v[i].first][v[i].second]!=mp[v[len-i-1].first][v[len-i-1].second]) flg=0;}
	//if (isp(tmp)||flg) cerr << tmp << endl;
	return isp(tmp)||flg;
}
void drp () {
	for (auto x:v) {mp[x.first][x.second]=-1;}
	for (int j=1;j<=m;j++) {
		int cnt=n;
		for (int i=n;i>=1;i--) {
			if (mp[i][j]!=-1) {mp[cnt--][j]=mp[i][j];}
		}
		while (cnt) {mp[cnt--][j]=-1;}
	}
}

bool dfs (int d) {
	int tmp[11][11],flg=0;
	for (int i=1;i<=10;i++) {
		for (int j=1;j<=10;j++) {flg|=(mp[i][j]>=0);tmp[i][j]=mp[i][j];}
	}
	if (!flg) {return 1;}
	for (int i=1;i<=200/d;i++) {
		v.clear();
		sr();
		if (chkk()) {
			ans.push_back(v);
			drp();
			if (dfs(d+1)) {return 1;}
			ans.pop_back();
			for (int i=1;i<=10;i++) {
				for (int j=1;j<=10;j++) {mp[i][j]=tmp[i][j];}
			}
		}
	}
	return 0;
}

int main () {
	freopen("game2.in","r",stdin);
	freopen("game2.out","w",stdout);
	srand(time(0));
	sd=rand()+1;
	scanf("%d%d%d%d%d%d%d%d",&n,&m,&k,&l1,&l2,&c1,&c2,&f);
	for (int i=1;i<=n;i++) {
		for (int j=1;j<=m;j++) {scanf("%d",&mp[i][j]);}
	}
	cerr << dfs(1) << endl;
	printf("%d\n",ans.size());
	for (auto v:ans) {
		printf("%d ",v.size());
		for (auto x:v) {printf("%d %d ",x.first,x.second);}
		printf("\n");
	}
	return 0;
}

测试点 3：

$n=m=100,\ K=500,\ l_{min}=2,\ l_{max}=18,\ c_1=2,\ c_2=0,\ F=0$，网格随机。

我们发现，想要得到最大的分数，只需要每次选出的都是一个 $18$ 位素数即可，由于素数密度是 $1/\ln n$ 级别，所以只要每次暴力随机一条路径，用 MR 判一下是不是素数就可以了， $500\times 18=9000$ ，比 $10000$ 小不少，可以轻松出解。

测试点 4：

$n=m=100,\ K=500,\ l_{min}=15,\ l_{max}=18,\ c_1=2,\ c_2=0,\ F=0$，网格随机。

同测试点 3，以下是这两个点的程序。

#include <bits/stdc++.h>
#define ll long long
#define ull unsigned long long
using namespace std;
const int N=110;
int n,m,k,l1,l2,c1,c2,f,mp[N][N],vis[N][N],dir[4][2]={{0,1},{0,-1},{1,0},{-1,0}};
vector < pair<int,int> > v; 
ull sd;
ull rd () {sd^=(sd<<27);sd^=(sd>>19);sd^=(sd<<25);return sd;}


ll qmul (ll a,ll b,ll p) {return (a*b-(ll)((long double)a/p*b)*p+p)%p;}
ll qpow (ll a,ll b,ll p) {
	ll res=1;
	while (b) {
		if (b&1) {res=qmul(res,a,p);}
		a=qmul(a,a,p),b>>=1;
	}
	return res;
}
bool mr (ll p,ll x) {
	if (qpow(x,p-1,p)!=1) {return 0;}
	ll k=p-1;
	while (!(k&1)) {
		k>>=1;
		ll tmp=qpow(x,k,p);
		if (tmp==p-1) {return 1;}
		else if (tmp!=1) {return 0;}
	}
	return 1;
}
bool isp (ll p) {
	if (p==46856248255981||p==1) {return 0;}
	if (p==2||p==3||p==7||p==61||p==24251) {return 1;}
	return mr(p,2)&&mr(p,3)&&mr(p,7)&&mr(p,61)&&mr(p,24251);
}


bool chk (int x,int y) {return (x>0&&y>0&&x<=n&&y<=m&&mp[x][y]!=-1&&!vis[x][y]);}
void sr () {
	int x=rd()%n+1,y=rd()%m+1;
	while (mp[x][y]<=0) {x=rd()%n+1,y=rd()%n+1;}
	v.push_back(make_pair(x,y));vis[x][y]=1;
	for (int i=1;i<=17;i++) {
		int dr=rd()%4;
		for (int i=1;i<=4;i++) {
			if (!chk(x+dir[dr][0],y+dir[dr][1])) {dr=(dr+1)%4;}
		}
		if (!chk(x+dir[dr][0],y+dir[dr][1])) {break;}
		x+=dir[dr][0],y+=dir[dr][1];
		v.push_back(make_pair(x,y));vis[x][y]=1;
	}
	for (auto x:v) vis[x.first][x.second]=0;
}
bool chkk () {
	ll tmp=0;
	if (v.size()!=18) {return 0;}
	for (auto x:v) {tmp=tmp*10+mp[x.first][x.second];}
	cerr << tmp << endl;
	return isp(tmp);
}
void drp () {
	for (auto x:v) {mp[x.first][x.second]=-1;}
	for (int j=1;j<=m;j++) {
		int cnt=n;
		for (int i=n;i>=1;i--) {
			if (mp[i][j]!=-1) {mp[cnt--][j]=mp[i][j];}
		}
		while (cnt) {mp[cnt--][j]=-1;}
	}
}
int main () {
	freopen("game4.in","r",stdin);
	freopen("game4.out","w",stdout);
	srand(time(0));
	sd=rand()+1;
	scanf("%d%d%d%d%d%d%d%d",&n,&m,&k,&l1,&l2,&c1,&c2,&f);
	for (int i=1;i<=n;i++) {
		for (int j=1;j<=m;j++) {scanf("%d",&mp[i][j]);}
	}
	for (int i=1;i<=k;i++) {
		v.clear();
		while (1) {
			sr();
			if (!chkk()) {v.clear();}
			else {break;}
		}
		printf("%d ",v.size());
		for (auto x:v) {printf("%d %d ",x.first,x.second);}
		printf("\n");
		drp();
	}
	return 0;
}

测试点 5：

$n=m=10,\ K=100,\ l_{min}=2,\ l_{max}=8,\ c_1=c_2=2,\ F=0$，网格如下：

9 0 4 4 4 0 1 0 0 9
4 3 4 1 5 3 3 6 2 2
6 9 8 0 4 9 9 1 7 7
5 3 2 5 6 8 0 5 8 0
1 7 4 5 0 7 0 5 7 3
5 3 5 1 0 9 7 2 3 4
3 6 3 9 4 5 2 6 4 5
9 7 6 5 5 1 6 6 3 0
9 3 1 0 7 6 8 3 2 2
9 0 9 4 8 4 4 5 0 6

和测试点 2 的区别是 $c=2$ 且 $F=0$ ，那么不用消完，但是需要尽可能消比较长的段，我们只需要在测试点 2 的爆搜中限制只搜长度等于 $8$ 的路径，就可以得到大概 $7$ 分到 $9$ 分。

搜出一个包含 $12$ 条长度为 $8$ 的路径的解，这时还剩 $4$ 个元素，如果运气好的话（多试几次）还能再找到一条长度为 $3$ 或者 $4$ 的路径，手动把它加上，就可以通过了。

测试点 6：

$n=m=1000,\ K=1,\ l_{min}=2,\ l_{max}=1000,\ c_1=0,\ c_2=1,\ F=0$，网格只包含 $1,2$ ，随机生成。

翻译一下，其实就是找到一条长度不超过 $1000$ 的尽量长的回文简单路径。

那么暴搜即可，每次随机一个中心，然后往两边扩展，很容易找到长度恰好为 $1000$ 的回文路径。

测试点 7：

$n=m=1000,\ K=1,\ l_{min}=2,\ l_{max}=1000,\ c_1=0,\ c_2=1,\ F=0$，网格只包含 $2,3,4$ ，随机生成。

同测试点 6，以下是这两个点的程序。

#include <bits/stdc++.h>
#define ll long long
#define ull unsigned long long
using namespace std;
const int N=1010;
int n,m,k,l1,l2,c1,c2,f,mp[N][N],vis[N][N],dir[4][2]={{0,1},{0,-1},{1,0},{-1,0}};
vector < pair<int,int> > v1,v2; 
ull sd;
ull rd () {sd^=(sd<<27);sd^=(sd>>19);sd^=(sd<<25);return sd;}


bool chk (int x,int y) {return (x>0&&y>0&&x<=n&&y<=m&&mp[x][y]!=-1&&!vis[x][y]);}
bool dfs (int x1,int y1,int x2,int y2,int v) {
	//cout << x1 << "  " << y1 << "  " << x2 << "  "  << y2 << "  " << v << endl;
	v1.push_back(make_pair(x1,y1)),v2.push_back(make_pair(x2,y2));
	vis[x1][y1]=vis[x2][y2]=1;
	if (v==500) {return 1;}
	for (int i=0;i<=3;i++) {
		for (int j=0;j<=3;j++) {
			int x3=x1+dir[i][0],y3=y1+dir[i][1],x4=x2+dir[j][0],y4=y2+dir[j][1];
			if (chk(x3,y3)&&chk(x4,y4)&&mp[x3][y3]==mp[x4][y4]) {
				if (dfs(x3,y3,x4,y4,v+1)) {return 1;}
			}
		}
	}
	v1.pop_back(),v2.pop_back();
	vis[x1][y1]=vis[x2][y2]=0;
	return 0;
}
bool solve () {
	int x=rd()%n+1,y=rd()%m+1,d=rd()%4,x2=x+dir[d][0],y2=y+dir[d][1];
	while (!chk(x,y)||!chk(x2,y2)||mp[x][y]!=mp[x2][y2]) {
		x=rd()%n+1,y=rd()%m+1,d=rd()%4,x2=x+dir[d][0],y2=y+dir[d][1];
	}
	return dfs(x,y,x2,y2,1);
}


int main () {
	freopen("game7.in","r",stdin);
	freopen("game7.out","w",stdout);
	srand(time(0));
	sd=rand()+1;
	scanf("%d%d%d%d%d%d%d%d",&n,&m,&k,&l1,&l2,&c1,&c2,&f);
	for (int i=1;i<=n;i++) {
		for (int j=1;j<=m;j++) {scanf("%d",&mp[i][j]);}
	}
	while (!solve());
	printf("1000 ");
	for (int i=1;i<=500;i++) {printf("%d %d ",v1[500-i].first,v1[500-i].second);}
	for (int i=1;i<=500;i++) {printf("%d %d ",v2[i-1].first,v2[i-1].second);}
	return 0;
}

测试点 8：

$n=999,\ m=100,\ K=1,\ l_{min}=2,\ l_{max}=100000,\ c_1=0,\ c_2=1,\ F=0$，网格似乎很有规律。

这个点和 $6,7$ 不同的是我们需要找出的回文串非常长，不可能直接搜索，而是需要构造。

但是我们可以发现，网格几乎只由 $5,6$ 构成，并且如果 $i+j$ 是奇数那么 $(i,j)$ 上几乎都是 $6$ ； $i+j$ 是偶数那么 $(i,j)$ 上几乎都是 $5$ ，只有极少的反例（大概 $200$ 多个位置）。

我们称这些反例所在的位置是坏位置，其他位置是好位置。

那么如果一个长度为奇数的路径经过的都是好位置，则它是回文的，这点非常容易证明（它必是 $5,6$ 交替的一条路径），所以我们找到一个尽可能长的这种好路径即可。

我们可以两行两行构造，在相邻的两行中通过来回绕经过大部分格子，同时避开所有坏位置，如图中蓝色路径：

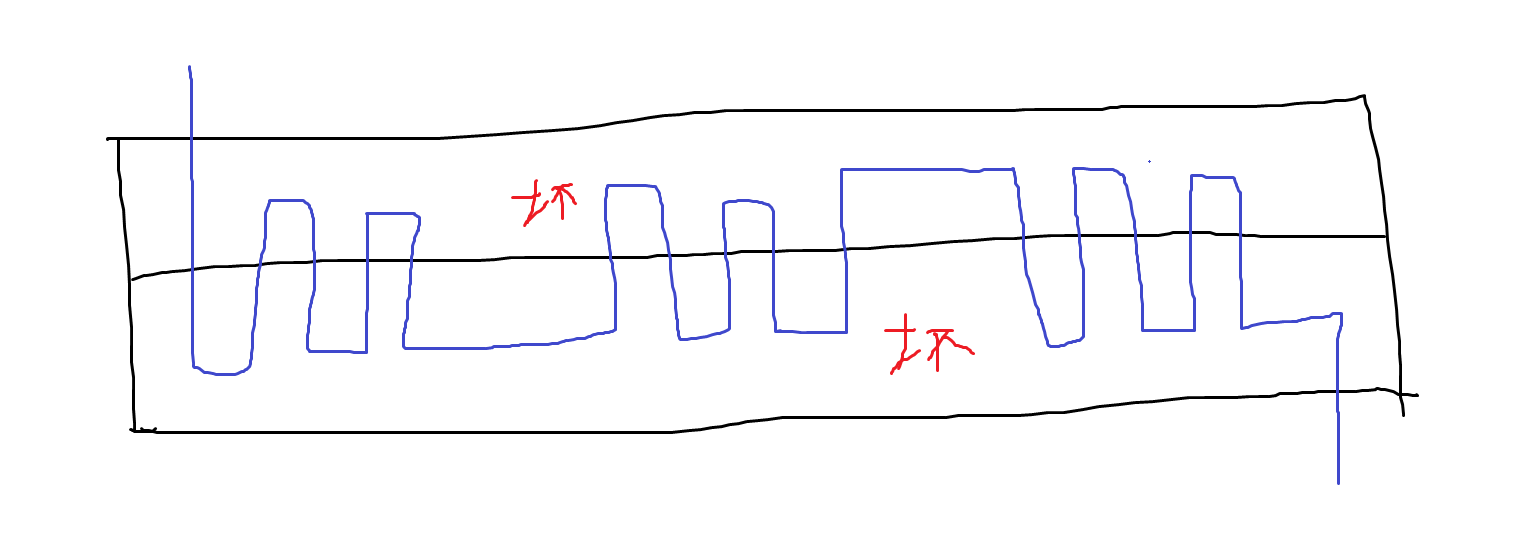
这做法看起来很好，但是有个 bug，就是如果两个坏位置把路给堵上了，就走不过去了。这时我们可以从旁边一行借个道，如图：

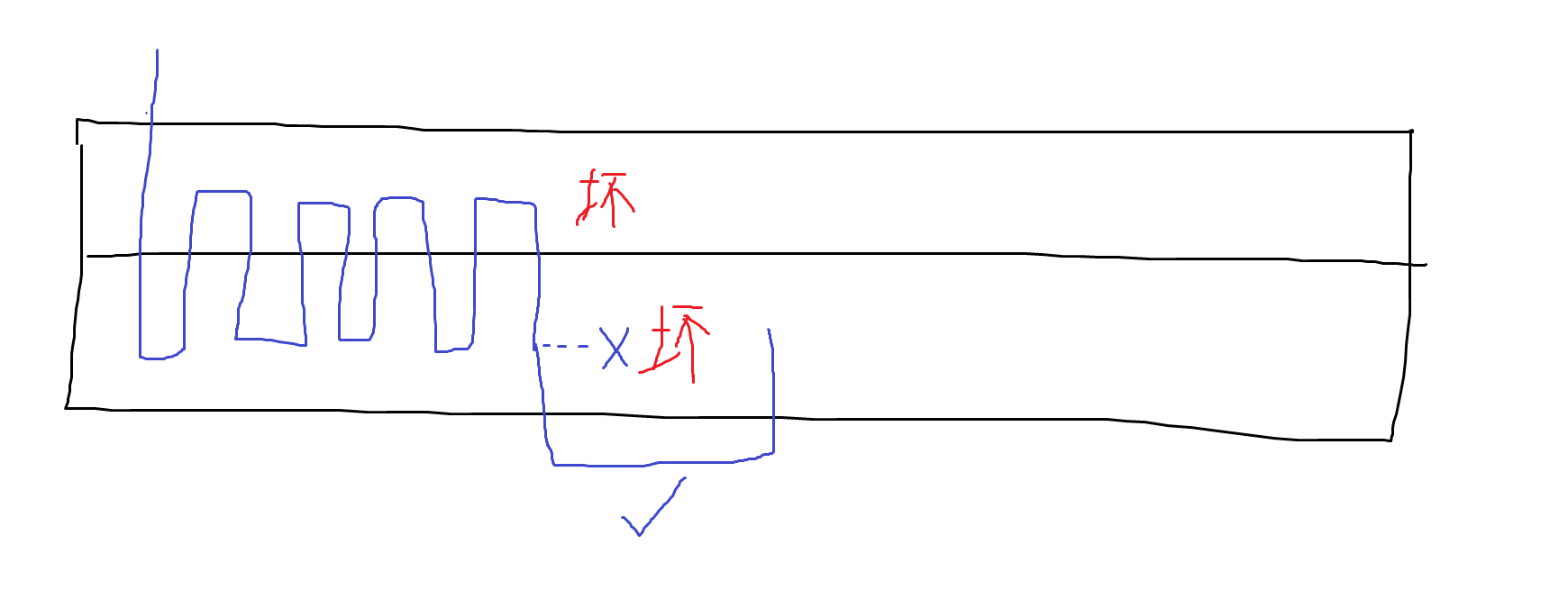
数据中只有 $3$ 个这样的情况，全都特判掉就行了（代码实现时因为一些原因，将行列互换了），最后构造出的长度是 $99475$ 。

#include <bits/stdc++.h>
#define ll long long
#define ull unsigned long long
using namespace std;
const int N=1010;
int n,m,k,l1,l2,c1,c2,f,mp[N][N],vis[N][N],dir[4][2]={{0,1},{1,0},{0,-1},{-1,0}};
vector < pair<int,int> > v; 
ull sd;
ull rd () {sd^=(sd<<27);sd^=(sd>>19);sd^=(sd<<25);return sd;}


bool chk (int x,int y) {return (x>0&&y>0&&x<=n&&y<=m&&mp[x][y]!=-1&&!vis[x][y]);}
void solve (int l,int x,int d) {
	if (l==101) {return;}
	//cerr << x << "  " << l << endl;
	assert(vis[x][l]==0);
	v.push_back(make_pair(x,l));
	vis[x][l]=1;
	if (x==818&&l==19) {solve(l+1,x,d);return;}
	if (x==818&&l==20) {
		v.push_back(make_pair(818,21));vis[818][21]=1;
		v.push_back(make_pair(817,21));vis[817][21]=1;
		v.push_back(make_pair(816,21));vis[816][21]=1;
		solve(l,x-2,d);return;
	}
	if (x==235&&l==76) {
		v.push_back(make_pair(235,77));vis[235][77]=1;
		v.push_back(make_pair(234,77));vis[234][77]=1;
		v.push_back(make_pair(233,77));vis[233][77]=1;
		solve(l,x-2,d);return;
	}
	if (x==269&&l==77) {solve(l+1,x,d);return;}
	if (x==269&&l==78) {
		v.push_back(make_pair(269,79));vis[269][79]=1;
		v.push_back(make_pair(270,79));vis[270][79]=1;
		v.push_back(make_pair(271,79));vis[271][79]=1;
		solve(l,x+2,d);return;
	}
	if (d==0) {
		if (x==n) {
			if (l&1) {solve(l+1,x,0);}
			else {solve(l+1,x,1);}
		} else if (l&1) {
			if (chk(x,l+1)&&chk(x+1,l+1)) {solve(l+1,x,d);}
			else {solve(l,x+1,d);}
		} else {
			if (chk(x,l-1)&&chk(x+1,l-1)) {solve(l-1,x,d);}
			else {solve(l,x+1,d);}
		}
	} else {
		if (x==1) {
			if (l&1) {solve(l+1,x,1);}
			else {solve(l+1,x,0);}
		} else if (l&1) {
			if (chk(x,l+1)&&chk(x-1,l+1)) {solve(l+1,x,d);}
			else {solve(l,x-1,d);}
		} else {
			if (chk(x,l-1)&&chk(x-1,l-1)) {solve(l-1,x,d);}
			else {solve(l,x-1,d);}
		}
	}
}


int main () {
	freopen("game8.in","r",stdin);
	freopen("game8.out","w",stdout);
	srand(time(0));
	sd=rand()+1;
	scanf("%d%d%d%d%d%d%d%d",&n,&m,&k,&l1,&l2,&c1,&c2,&f);
	for (int i=1;i<=n;i++) {
		for (int j=1;j<=m;j++) {
			scanf("%d",&mp[i][j]);
			if ((i+j)&1) {
				if (mp[i][j]!=6) {vis[i][j]=1;cout << i << "  " << j << endl;}
			} else {
				if (mp[i][j]!=5) {vis[i][j]=1;cout << i << "  " << j << endl;}
			}
		}
	}
	solve(1,1,0);
	if (v.size()%2==0) {v.pop_back();}
	printf("%d ",v.size());
	for (auto x:v) {assert(x.second<=100);printf("%d %d ",x.first,x.second);}
	return 0;
}

测试点 9：

$n=129,\ m=128,\ K=5,\ l_{min}=2,\ l_{max}=20000,\ c_1=0,\ c_2=2,\ F=0$，网格似乎很有规律。

虽然 $K=5$ ，但是由于分数是根据平方计算，所以我们还是希望一条路径搞定，这样路径最长，分数最大。

用比较好的编辑器打开输入数据后可以观察到每行都几乎是回文的，于是我们可以发现，整个网格几乎关于中轴线对称，只有 $18$ 对位置例外。

那么和测试点 8 就差不多了，我们只考虑左半边，只要绕开这些不对称的坏位置，然后再把左半边的路径翻折到右半边，就一定是一条回文的路径了。

这个测试点由于坏位置很少，所以甚至不需要测试点 8 那样的特判，直接两行两行绕就可以了，最后构造出的长度是 $16440$ 。

#include <bits/stdc++.h>
#define ll long long
#define ull unsigned long long
using namespace std;
const int N=1010;
int n,m,k,l1,l2,c1,c2,f,mp[N][N],vis[N][N],dir[4][2]={{0,1},{0,-1},{1,0},{-1,0}};
vector < pair<int,int> > v; 
ull sd;
ull rd () {sd^=(sd<<27);sd^=(sd>>19);sd^=(sd<<25);return sd;}
bool chk (int x,int y) {return (x>0&&y>0&&x<=n&&y<=m&&mp[x][y]!=-1&&!vis[x][y]);}
void solve (int l,int x,int d) {
	if (l==65) {return;}
	v.push_back(make_pair(x,l));
	vis[x][l]=1;
	if (d==0) {
		if (x==n) {
			if (l&1) {solve(l+1,x,0);}
			else {solve(l+1,x,1);}
		} else if (l&1) {
			if (chk(x,l+1)&&chk(x+1,l+1)) {solve(l+1,x,d);}
			else {solve(l,x+1,d);}
		} else {
			if (chk(x,l-1)&&chk(x+1,l-1)) {solve(l-1,x,d);}
			else {solve(l,x+1,d);}
		}
	} else {
		if (x==1) {
			if (l&1) {solve(l+1,x,1);}
			else {solve(l+1,x,0);}
		} else if (l&1) {
			if (chk(x,l+1)&&chk(x-1,l+1)) {solve(l+1,x,d);}
			else {solve(l,x-1,d);}
		} else {
			if (chk(x,l-1)&&chk(x-1,l-1)) {solve(l-1,x,d);}
			else {solve(l,x-1,d);}
		}
	}
}
int main () {
	freopen("game9.in","r",stdin);
	freopen("game9.out","w",stdout);
	srand(time(0));
	sd=rand()+1;
	scanf("%d%d%d%d%d%d%d%d",&n,&m,&k,&l1,&l2,&c1,&c2,&f);
	for (int i=1;i<=n;i++) {
		for (int j=1;j<=m;j++) {scanf("%d",&mp[i][j]);}
		for (int j=1;j<=64;j++) {
			if (mp[i][j]!=mp[i][129-j]) {vis[i][j]=1;printf("%d  %d\n",i,j);}
		}
	}
	cout << endl;
	solve(1,1,0);
	for (int i=1;i<=n;i++) {
		for (int j=1;j<=64;j++) {
			if (!vis[i][j]) {printf("%d  %d\n",i,j);}
		}
	}
	printf("%d ",2*v.size());
	for (auto x:v) {assert(x.second<=100);printf("%d %d ",x.first,x.second);}
	reverse(v.begin(),v.end());
	for (auto x:v) {assert(x.second<=100);printf("%d %d ",x.first,129-x.second);}
	return 0;
}

测试点 10：

$n=3,\ m=999,\ K=10,\ l_{min}=2,\ l_{max}=2997,\ c_1=0,\ c_2=2,\ F=0$，网格似乎很有规律。

和测试点 9 一样，我们还是希望一条路径搞定，这里 $l_{max}=2997=n\times m$ ，所以最好是一条路径覆盖所有数。

继续观察网格规律，首先可以发现的是如果将每行三个数三个数划分，将每行看成 $333$ 个三元组构成的序列，则这个序列是回文的。

进一步观察，我们可以输出每个三元组的第一个数，发现每一行关于第一个数都是有周期的。

也就是说，整个网格有如下周期：

1 2 1 2 3 2 3 4 3 4 5 4 5 6 5 4 5 4 3 4 3 2 3 2 1 2 1
4 3 2 5 4 3 6 5 4 7 6 5 8 7 6 7 6 5 6 5 4 5 4 3 4 3 2
5 4 3 6 5 4 7 6 5 8 7 6 9 8 7 8 7 6 7 6 5 6 5 4 5 4 3

观察每行每个三元组的第一个数，第一行是 1 2 3 4 5 4 3 2 1，第二行是 4 5 6 7 8 7 6 5 4，第三行是 5 6 7 8 9 8 7 6 5，有很强的对称性，于是我们尝试对于这个周期解决子问题。

通过尝试或者暴搜，我们发现有一组规律性很强的解，它的前 $9$ 项就是 1 2 3 4 5 4 3 2 1，你能找到吗？

没错！它就藏在第一个 $3\times 3$ 块中：

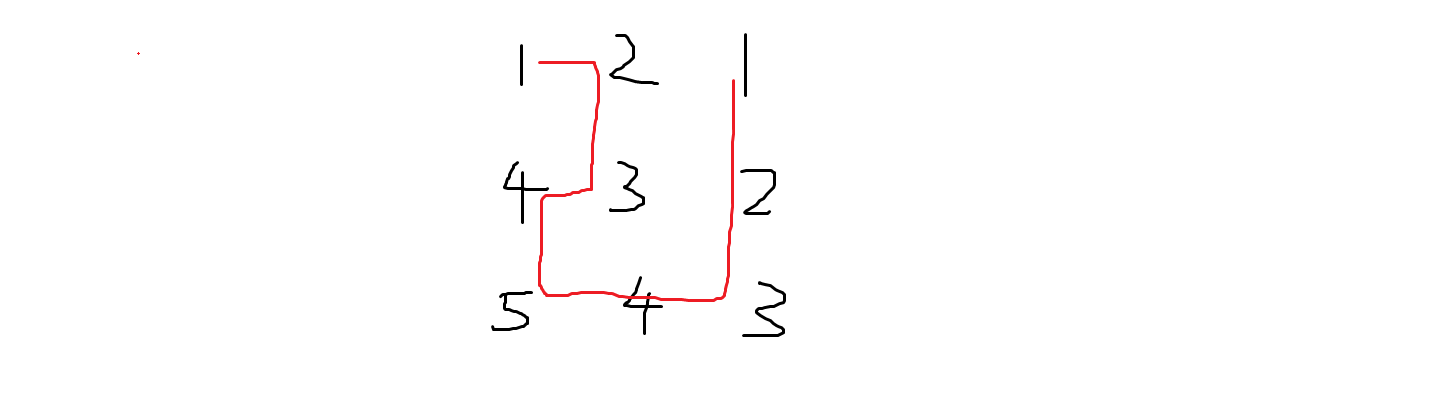
于是我们发现只要将每个 $3\times 3$ 块都像这样连起来，再把所有块串一起，就是一组合法的解。

#include <bits/stdc++.h>
#define ll long long
#define ull unsigned long long
using namespace std;
const int N=1010;
int n,m,k,l1,l2,c1,c2,f,mp[N][N];
int main () {
	freopen("game10.in","r",stdin);
	freopen("game10.out","w",stdout);
	scanf("%d%d%d%d%d%d%d%d",&n,&m,&k,&l1,&l2,&c1,&c2,&f);
	for (int i=1;i<=n;i++) {
		for (int j=1;j<=m;j++) {scanf("%d",&mp[i][j]);}
	}
	printf("2997\n");
	for (int i=1;i<=333;i++) {
		printf("%d %d %d %d %d %d %d %d ",1,i*3-2,1,i*3-1,2,i*3-1,2,i*3-2);
		printf("%d %d %d %d %d %d %d %d %d %d ",3,i*3-2,3,i*3-1,3,i*3,2,i*3,1,i*3);
	}
	return 0;
}

ID

4583

时间

1000ms

内存

125MiB

难度

标签

递交数

已通过

上传者

Hydro

1 条题解

自动搬运

以下是正文

NOI 2014 消除游戏

题目大意：

测试点 1：

测试点 2：

测试点 3：

测试点 4：

测试点 5：

测试点 6：

测试点 7：

测试点 8：

测试点 9：

测试点 10：

[NOI2014] 消除游戏

信息

1 条题解

自动搬运

以下是正文

NOI 2014 消除游戏

题目大意：

测试点 1：

测试点 2：

测试点 3：

测试点 4：

测试点 5：

测试点 6：

测试点 7：

测试点 8：

测试点 9：

测试点 10：

[NOI2014] 消除游戏

信息

还没有账户？

登录