自动搬运

查看原文

来自洛谷，原作者为

	Hope2075 时间的流沙，淹没梦境里的夏

搬运于2025-08-24 22:08:44，当前版本为作者最后更新于2020-06-20 11:00:06，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

upd:既然已经决定用解析几何暴力求了，就暴力到底吧QWQ

以下是废话

去年比赛时做了这道题，写模拟退火被卡精度，只有30分

当时就想试试用最小覆盖圆的思路，每一步用解析式直接求圆的圆心坐标和半径

然后我想了一下，一般情况需要求3条双曲线的交点（根据性质，应该至少有一个公共交点），也就是解二元二次方程，而且消元很麻烦，就放弃了

今年突然心血来潮，便尝试求了一下，发现并没有那么复杂，就用新的做法A了这道题，而且抢了最优解(2020-06-20 10:32:54 69ms)

下面是具体思路

基本思路

按照点的最小圆覆盖的做法求这些圆的最小圆覆盖，也就是P1742

最小圆覆盖：用的随机增量法，进行$n$步，每一步加入一个点。如果这个点在之前$i-1$个点的最小覆盖圆内部，那么就跳过。否则这个点必定在前$i$个点的最小覆盖圆上，枚举之前$i-1$个点组成的点对即可

如果把上面的“点”换成“圆”，也成立，所以可以用类似的思路做这道题

复杂度和点的最小覆盖圆相同，参考那道题的证明即可（常数大一些）

另外，在求交点时可以发现一个特殊的性质，就能简化计算

具体做法

以下设三个圆分别为

$O_1(x_1,y_1),r_1$

$O_2(x_2,y_2),r_2$

$O_3(x_3,y_3),r_3$

求一个圆的最小圆覆盖

很明显，取这个圆本身就行

求两个圆的最小圆覆盖

(两个圆的圆心分别是$O_1$和$O_2$)

分为两种情况

第一种：两圆半径相等

那么圆心就是两圆圆心连线的中点，半径就是圆心距离的一半加上一个圆的半径

表示出来就是：

$O(\frac{x_1+x_2}{2},\frac{y_1+y_2}{2}),r=\frac{1}{2}|O_1O_2|+r_1$

（图略，应该很好画）

第二种：两圆半径不相等

这时候圆心到两圆的距离之差就是半径之差，而且圆心更靠近大圆

也就是这样

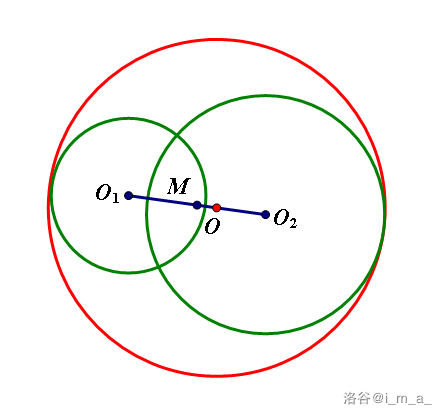
圆心到中点的距离就是半径差的一半

先把中点坐标求出来，再偏移一下就行

半径就用到某个圆心的距离加上那个圆的半径

表示出来就是

$M(\frac{x_1+x_2}{2},\frac{y_1+y_2}{2}),\vec{MO}=\frac{(r_2-r_1)\vec{O_1O_2}}{2|\vec{O_1O_2}|},r=|OO_1|+r_1$

求三个圆的最小圆覆盖

如果某两个圆是包含关系，那么求两个圆的最小圆覆盖即可，而且算法可以保证不会出现这种情况

理论上要分三种情况，但实际有两种可以合并

第一种：三个圆半径均相等

这时候求三角形的外接圆，把半径加上某个圆的半径即可

求外接圆的办法可以参考最小圆覆盖的题解

可以发现这样的圆恰好与这三个圆均内切

也就是这样

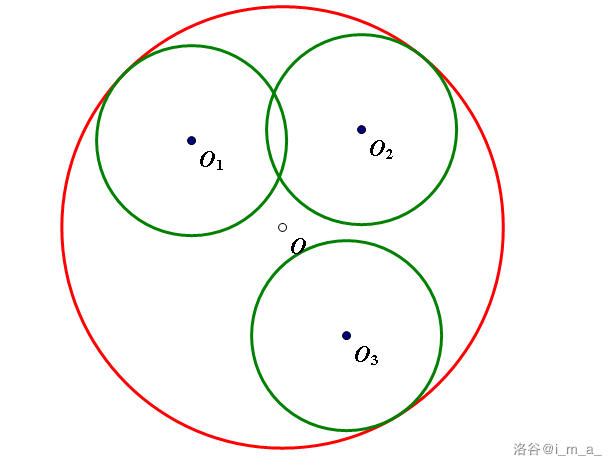
第二种：存在两个圆半径不相等

这时候对于某两个圆而言，满足条件的圆的圆心在一条直线或双曲线上

方程就是$\sqrt{(x-x_1)^2+(y-y_1)^2}+r_1=\sqrt{(x-x_2)^2+(y-y_2)^2}+r_2$

如果两圆半径相等，那么这个方程表示中垂线，否则就表示双曲线（已经限制任意两圆不能是包含关系了）

画出来大概这样（第一个是存在两圆半径相等的情况）

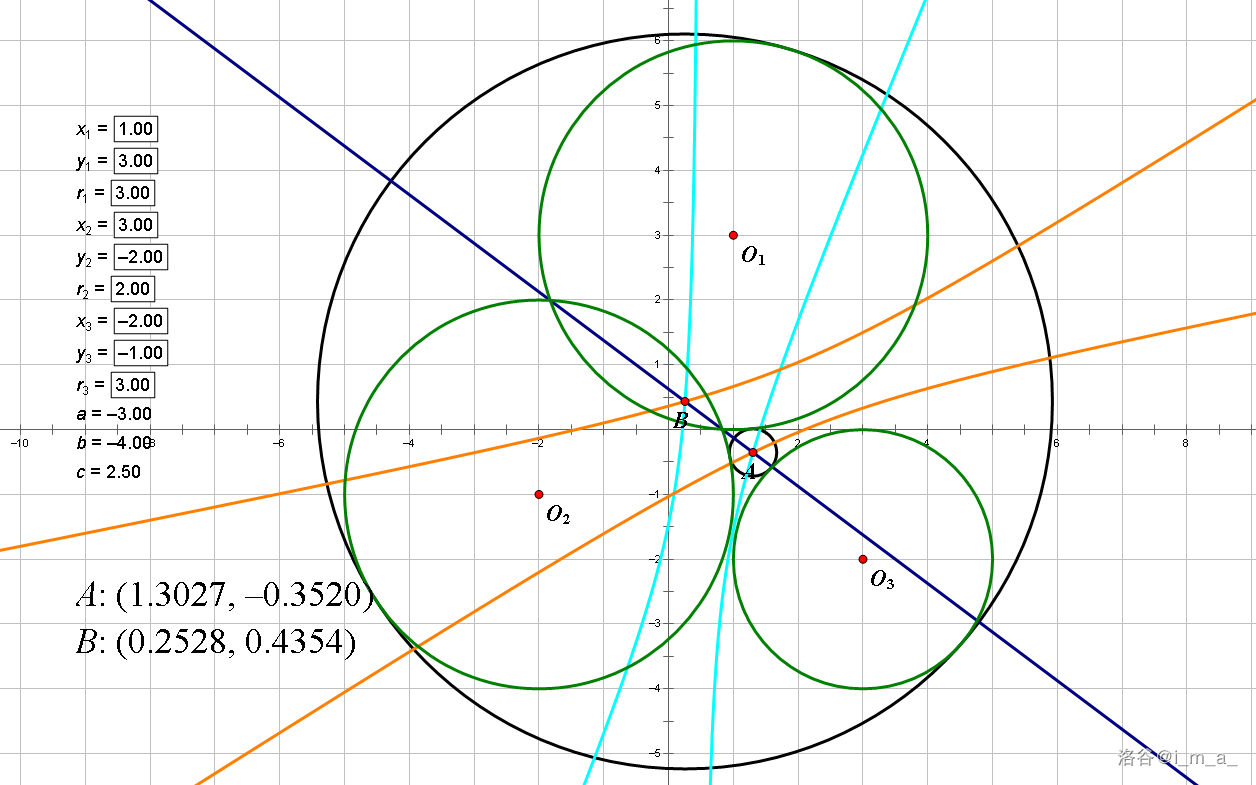
注意图中的深蓝色直线，它有特殊含义，下面会进行叙述

首先，设$A_i=(x-x_i)^2+(y-y_i)^2$

那么方程可以表示为$\sqrt{A_1}+r_1=\sqrt{A_2}+r_2$

可以化为$\sqrt{A_1}-\sqrt{A_2}=r_2-r_1$

分子有理化，再取倒数，得$\sqrt{A_1}+\sqrt{A_2}=\frac{A_1-A_2}{r_2-r_1}$

相加，得$2\sqrt{A_1}=\frac{A_1-A_2}{r_2-r_1}+r_2-r_1$

先不要着急平方，再写一个式子

$2\sqrt{A_1}=\frac{A_1-A_3}{r_3-r_1}+r_3-r_1$

所以$\frac{A_1-A_2}{r_2-r_1}+r_2-r_1=\frac{A_1-A_3}{r_3-r_1}+r_3-r_1$

可以看出这是一次方程，也就是图中的深蓝色直线

继续化简，设直线方程为$ax+by+c=0$，那么

$a=\left|\begin{array}{cccc} x_1 & r_1 & 1 \\ x_2 & r_2 & 1\\ x_3 & r_3 & 1 \end{array}\right|$

$b=\left|\begin{array}{cccc} y_1 & r_1 & 1 \\ y_2 & r_2 & 1\\ y_3 & r_3 & 1 \end{array}\right|$

$c=-\frac{1}{2}\left|\begin{array}{cccc} x_1^2+y_1^2-r_1^2 & r_1 & 1 \\ x_2^2+y_2^2-r_2^2 & r_2 & 1\\ x_3^2+y_3^2-r_3^2 & r_3 & 1 \end{array}\right|$

这样，所求圆的圆心也在这条直线上

接下来把原来双曲线的方程也化简一下（平方再整理就行，但整理很麻烦）

设双曲线的方程是$Ax^2+Bxy+Cy^2+Dx+Ey+F=0$

$A=4[(x_1-x_2)^2+(r_1-r_2)^2]$

$B=8(x_1-x_2)(y_1-y_2)$

$C=4[(y_1-y_2)^2+(r_1-r_2)^2]$

$D=4[(x_1+x_2)(r_1-r_2)^2-(x_1-x_2)(x_1^2+y_1^2-x_2^2-y_2^2)]$

$E=4[(y_1+y_2)(r_1-r_2)^2-(y_1-y_2)(x_1^2+y_1^2-x_2^2-y_2^2)]$

$F=(x_1^2+y_1^2-x_2^2-y_2^2)^2-2(x_1^2+y_1^2+x_2^2+y_2^2)(r_1-r_2)^2+(r_1-r_2)^4$

可以代入消元解方程组求坐标

用直线方程消元后得到一个二次方程，用$x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}$求根，再带入直线方程求出另一个坐标就行

注意直线方程的系数可能为0，需要判断一下

这时会发现有两个解，原因就是平方化简时出现了增根

另一个解恰好是与三个圆分别外切的圆的圆心

但我们需要选出其中一个，这时计算圆心到两个点的距离，比较大小关系就能确定这个根是不是需要的点（目标点距离较大的圆更远）

这样求出来的坐标和半径理论上就没有任何误差（但会受计算机精度限制）

暴力解方程

暴力要彻底

为了防止混淆，令

$A=\left|\begin{array}{cccc} x_1 & r_1 & 1 \\ x_2 & r_2 & 1\\ x_3 & r_3 & 1 \end{array}\right|$

$B=\left|\begin{array}{cccc} y_1 & r_1 & 1 \\ y_2 & r_2 & 1\\ y_3 & r_3 & 1 \end{array}\right|$

过程很繁琐，只说一下简单思路和解出的结果，具体过程全部省略

而且大部分解析式我并没有化简，只是猜的结论，但应该是对的

如果手动把系数代进去，会得到一个一元二次方程

解方程即可没这么简单

以下假设消去的是$y$

首先化简$x^2$的系数

通过化简，可以得到$4(r_1-r_2)^2(T^2-a^2-b^2)$

其中$T=\left|\begin{array}{cccc} x_1 & y_1 & 1\\ x_2 & y_2 & 1\\ x_3 & y_3 & 1 \end{array}\right|$

可以想到，$(r_1-r_2)^2$可以消掉，否则交换两个点的顺序，结果就会不同

然后化简$x$的系数

明确了变形的方向就会简单一点，可以先把不含$(r_1-r_2)^2$的项合并，然后再和剩余部分合并，而且结果应该是交换任意两个点后保持不变的（也就是有对称性）

结果是$4(r_1-r_2)^2(x_1m_1n_1+x_2m_2n_2+x_3m_3n_3)$

其中$m_1=[(x_2-x_3)^2+(y_2-y_3)^2-(r_2-r_3)^2]$

$n_1=[(x_1-x_2)(x_3-x_1)+(y_1-y_2)(y_3-y_1)-(r_1-r_2)(r_3-r_1)]$

$m_2,n_2,m_3,n_3$类似

接下来似乎要求常数项的系数

但是考虑一下，就能找到更简便的方法

考虑二次方程求根方程：

$x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}$

求$b^2-4ac$就行（看起来复杂，实际上比化简系数再乘起来要简单）

根据前面的结果，可以求出两个解对应圆的圆心连线中点的坐标，而两个解则是这个点在直线上移动了一段距离

可以想到对于$x$和$y$的方程，后面$\pm\sqrt{b^2-4ac}$项分别含有因子$B$和$A$，并且均含$(r_1-r_2)^2$因子

按照上面的思路化简即可（最好先消掉因子$A$或$B$，这样较为简单）

可以得到$b^2-4ac=16B^2m_1m_2m_3(r_1-r_2)^2$（对于$x$）

表示出来的时候，应该是一个$\pm$，一个$\mp$

另一个问题：如何确定符号？

可以把半径也暴力求出来，求的时候就会发现根号限定了代入的$\pm$应该取哪一个（求出的结果应当对称）

（算到最后我没耐心化简了，就根据式子猜了几个结论，代数检验了一下）

最终结果：

$(\frac{U(x_1,x_2,x_3)+B\sqrt{\Delta}}{U(1,1,1)},\frac{U(y_1,y_2,y_3)-A\sqrt{\Delta}}{U(1,1,1)}),R=\frac{U(r_1,r_2,r_3)-T\sqrt{\Delta}}{U(1,1,1)}$

要求$T>0$。如果$T=0$，则三点共线。如果$T<0$，那么任意交换一对点后再算即可，或者改变符号也行

可以看出，对于半径两两相等的情况也适用

这样理论上可以运行得很快（用中间变量保留相同的值，每次计算只有一次开根号），而且可以用一些特殊方法做到任意精度

但测试时好像评测机性能不稳定，有些点会慢一点，总用时大约0.2s

求最终答案

和点的最小圆覆盖基本一样，只要把求两点或三点的最小覆盖圆换成相应圆的做法就行

关于特判

我想了一下，应该需要特判三个圆的情况（有时候只和两个圆相切就能盖住三个圆），否则可以手动造几组数据卡掉，但提交的时候没有WA，应该是因为数据随机

代码

这是没卡常的代码，基本就是按照上面的式子写的，用时405ms

（我在纸上推式子时就写的$x_1$之类的字母，为了省事，计算时没用结构体，调用函数时先把结构体拆开）

69ms的代码就看提交记录吧

主要是IO优化，另外计算过程也优化了一下

手动解方程的方法把对应部分换掉即可，应该比这个好写

#include<iostream>
#include<cmath>
struct C{
    double x,y,r;
    C(){x=0;y=0;r=0;}
    C(double x0,double y0,double r0){x=x0;y=y0;r=r0;}
};
unsigned long long seed=666;
int rand(int l){
    return (seed=(seed*998244353+65537))%l;
}
void swap(double &a,double &b){
	double t=a;a=b;b=t;
}
void swap(C &a,C &b){
	C t=a;a=b;b=t;
}
double dis(double x1,double y1,double x2,double y2){
    return sqrt((x1-x2)*(x1-x2)+(y1-y2)*(y1-y2));
}
bool inside(C a,C b){//a in b
    if(a.r>=b.r)return false;
    if(dis(a.x,a.y,b.x,b.y)<=fabs(a.r-b.r))return true;
    return false;
}
void cal(double x1,double y1,double r1,double x2,double y2,double r2,double &px,double &py,double &r){
    if(r1==r2){
        double rx=(x1+x2)/2;
        double ry=(y1+y2)/2;
        double rr=dis(x1,y1,x2,y2)/2+r1;
        px=rx;py=ry;r=rr;
    }else{
        double mx=(x1+x2)/2;
        double my=(y1+y2)/2;
        double dr=r2-r1;
        double d=dis(x1,y1,x2,y2);
        double rx=mx+(x2-x1)*dr/d/2;
        double ry=my+(y2-y1)*dr/d/2;
        double rr=dis(x1,y1,rx,ry)+r1;
        px=rx;py=ry;r=rr;
    }
    
}
C cal(C c1,C c2){
    C cr;
    cal(c1.x,c1.y,c1.r,c2.x,c2.y,c2.r,cr.x,cr.y,cr.r);
    return cr;
}
void cal(double x1,double y1,double r1,double x2,double y2,double r2,double x3,double y3,double r3,double &px,double &py,double &r){
	if(r1>r2){//冒泡排序，保证取两个半径不同的圆
		swap(x1,x2);
		swap(y1,y2);
		swap(r1,r2);
	}
	if(r2>r3){
		swap(x2,x3);
		swap(y2,y3);
		swap(r2,r3);
	}
	if(r1>r2){
		swap(x1,x2);
		swap(y1,y2);
		swap(r1,r2);
	}
	if(r1==r3){//如果三个圆的半径相同，那么最大值等于最小值
        double t=2*(x2-x1)*(y3-y1)-2*(x3-x1)*(y2-y1);
		double rx=((x2*x2+y2*y2-x1*x1-y1*y1)*(y3-y1)-(x3*x3+y3*y3-x1*x1-y1*y1)*(y2-y1))/t;
		double ry=-((x2*x2+y2*y2-x1*x1-y1*y1)*(x3-x1)-(x3*x3+y3*y3-x1*x1-y1*y1)*(x2-x1))/t;
        double rr=dis(x1,y1,rx,ry)+r1;
        px=rx;py=ry;r=rr;
	}else{//否则最大的圆和最小的圆半径不同
		double a=x1*(r2-r3)+x2*(r3-r1)+x3*(r1-r2);
		double b=y1*(r2-r3)+y2*(r3-r1)+y3*(r1-r2);
		double c=-0.5*((x1*x1+y1*y1-r1*r1)*(r2-r3)+(x2*x2+y2*y2-r2*r2)*(r3-r1)+(x3*x3+y3*y3-r3*r3)*(r1-r2));
		
		double A=4*((x1-x3)*(x1-x3)-(r1-r3)*(r1-r3));
		double B=8*(x1-x3)*(y1-y3);
		double C=4*((y1-y3)*(y1-y3)-(r1-r3)*(r1-r3));
		double D=4*((x1+x3)*(r1-r3)*(r1-r3)-(x1-x3)*(x1*x1-x3*x3+y1*y1-y3*y3));
		double E=4*((y1+y3)*(r1-r3)*(r1-r3)-(y1-y3)*(x1*x1-x3*x3+y1*y1-y3*y3));
		double F=(x1*x1-x3*x3+y1*y1-y3*y3)*(x1*x1-x3*x3+y1*y1-y3*y3)-2*(x1*x1+x3*x3+y1*y1+y3*y3)*(r3-r1)*(r3-r1)+(r3-r1)*(r3-r1)*(r3-r1)*(r3-r1);
		
        double rx1,rx2,ry1,ry2;
        if(fabs(b)>fabs(a)){//取系数绝对值较大的，避免除以0
            double xa=b*b*A-a*b*B+a*a*C;
            double xb=-b*c*B+2*a*c*C+b*b*D-a*b*E;
            double xc=c*c*C-b*c*E+b*b*F;
            
            double dx=xb*xb-4*xa*xc;
            rx1=(-xb+sqrt(dx))/(2*xa);
            rx2=(-xb-sqrt(dx))/(2*xa);
            
            ry1=-(c+a*rx1)/b;
            ry2=-(c+a*rx2)/b;
            
            
            
            
            
        }else{
            double ya=a*a*C-b*a*B+b*b*A;
            double yb=-a*c*B+2*b*c*A+a*a*E-b*a*D;
            double yc=c*c*A-a*c*D+a*a*F;
            
            double dy=yb*yb-4*ya*yc;
            ry1=(-yb+sqrt(dy))/(2*ya);
            ry2=(-yb-sqrt(dy))/(2*ya);
            
            rx1=-(c+b*ry1)/a;
            rx2=-(c+b*ry2)/a;
            
        }
        
        double d11=dis(rx1,ry1,x1,y1);
        double d13=dis(rx1,ry1,x3,y3);
            
        double d21=dis(rx2,ry2,x1,y1);
            
        if(d11>d13){
            double rr1=d11+r1;
            px=rx1;py=ry1;r=rr1;
        }else{
            double rr2=d21+r1;
            px=rx2;py=ry2;r=rr2;
        }
	}
}
C cal(C c1,C c2,C c3){
    C cr;
    cal(c1.x,c1.y,c1.r,c2.x,c2.y,c2.r,c3.x,c3.y,c3.r,cr.x,cr.y,cr.r);
    return cr;
}
int n;
C list[50007];
C cur;
int main(){
	std::ios::sync_with_stdio(false);
    std::cin>>n;
    for(int i=1;i<=n;i++){
        double x,y,r;
        std::cin>>x>>y>>r;
        list[i]=C(x,y,r);
    }
    for(int i=n;i>1;i--){
    //需要打乱顺序，这样才能保证复杂度
        int p=rand(i);
        swap(list[i],list[p+1]);
    }
    cur=list[1];
    for(int i=2;i<=n;i++){
        if(!inside(list[i],cur)){
            cur=list[i];
            for(int j=1;j<i;j++){
                if(!inside(list[j],cur)){
                    cur=cal(list[i],list[j]);
                    for(int k=1;k<j;k++){
                        if(!inside(list[k],cur)){
                            cur=cal(list[i],list[j],list[k]);
                        }
                    }
                }
            }
        }
    }
    std::cout<<cur.x<<" "<<cur.y<<" "<<cur.r<<std::endl;
}