自动搬运

查看原文

来自洛谷，原作者为

	NaCly_Fish 北海虽赊，扶摇可接。

搬运于2025-08-24 22:08:32，当前版本为作者最后更新于2019-03-02 23:15:53，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

这里写一种正经一点的解法吧：在线圆方树

既然是圆方树的模板，那我们就要建树 (废话)

圆方树的建点、连边规则是这样的：
1、原图中的点都是圆点
2、对于每个环，新建一个方点；这个方点和环上其它圆点连成菊花图
3、对于不在环上的两个圆点，保留原图中的边
根据仙人掌的性质，易证不存在相邻的两个方点。

别忘了，我们还要确定树的边权。
从一个点开始dfs，对于$u\rightarrow v$的边：

• 若$u,v$都是圆点，则权值为原图中边权
• 若$u$为方点，则权值为$v$到$u$父亲的最短路
• 否则权值为$0$

只是这么说，可能还不够清楚，放两张图来你们直观感受一下：
第一张这是原图，用红色加粗表示的是非树边

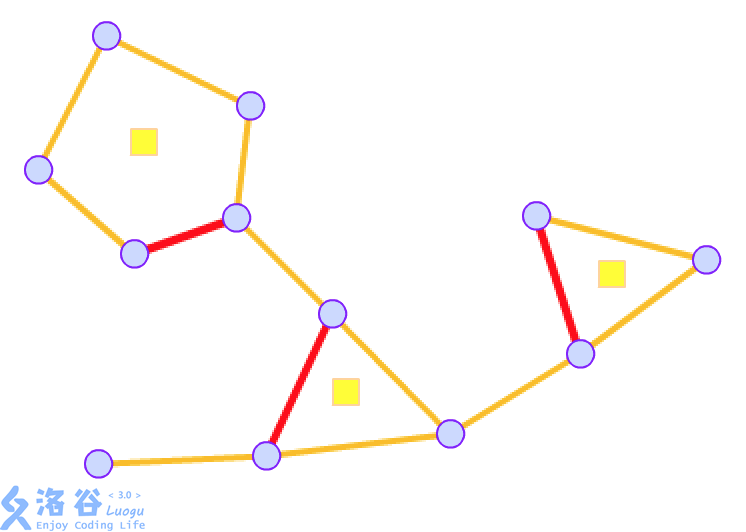
对于每个环，建一个方点，然后圆方树就搞好了：

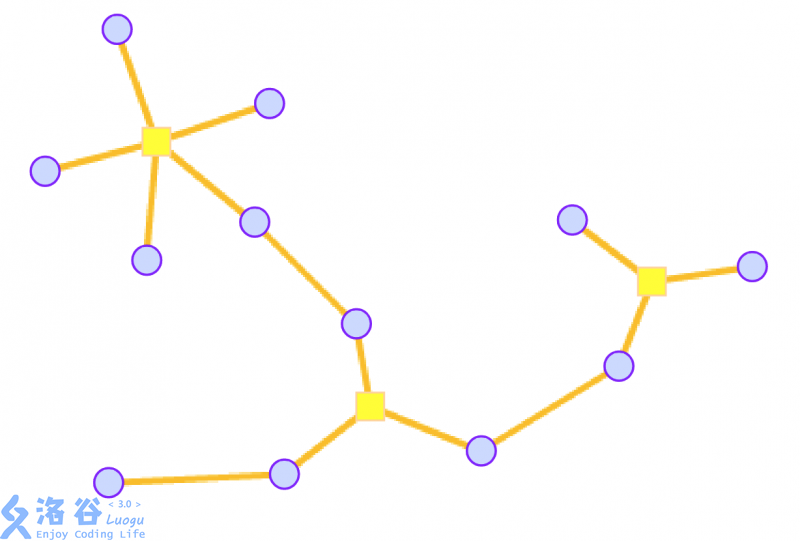
现在我们建好了树，就要考虑用它来求解啦qwq
和普通的求树上路径一样，我们在求$u\rightarrow v$的最短路时，要求出$\text{lca}(u,v)$，设其为$p$。
我们进行分类讨论：

• 若$p$为圆点，那答案就是树上这两点的距离
• 若$p$为方点，则需要找出$p$的两个儿子$A,B$，分别是$u$和$v$的祖先。由于$A,B$在一个环上，所以$\text{dis}(A,B)$可以直接求(两种情况取$\text{min}$)。此时答案为$\text{dis}(A,B)+\text{dis}(A,u)+\text{dis}(B,v)$

这题的主要思路大概就是这样了。
不过你也许会问：怎么找$p$的儿子$A,B$啊？
如果你用的是倍增，那很简单。在找$\text{lca}(u,v)$是顺便求出来就好了。
如果你用树剖，这里就稍微麻烦一点。
考虑$p$的儿子，只有两种情况：轻儿子或重儿子。
如果一个点是轻儿子，说明这个儿子是一个重链的顶点，从沿着重链一直向上跳就找到了。
如果在向上跳的过程中，发现跳过了$p$，那么要找的儿子就是重儿子。
时间复杂度$\Theta(q\log n)$

参考代码：

#include<cstdio>
#include<iostream>
#include<cstring>
#include<algorithm>
#include<cmath>
#include<vector>
#define ll long long
#define N 40003
using namespace std;

struct edge{
    int v,w;
    edge(int v=0,int w=0):v(v),w(w){}
};

vector<edge> g[N],adj[N];
int dfn[N],low[N],fa[N];
int top[N],son[N],size[N],dep[N],b[N],sum[N],dis[N];
int n,m,q,cnt,ext;

inline void read(int &x);
void print(int x);
void tarjan(int u,int f);
inline int min(int x,int y);
inline void solve(int u,int v,int w);
void dfs1(int u,int f);
void dfs2(int u,int f);
inline int lca(int u,int v); 
inline int find(int u,int f); //找到是u祖先的f的儿子

signed main(){
    int u,v,p,w,A,B,ans;
    read(n),read(m),read(q);
    ext = n; //ext 为 extra 的简写,表示额外的节点
    for(int i=1;i<=m;++i){
        read(u),read(v),read(w);
        g[u].push_back(edge(v,w));
        g[v].push_back(edge(u,w));
    }
    tarjan(1,0); //找环的同时建树
    dfs1(1,0);
    dfs2(1,1); //树剖的两遍dfs
    while(q--){
        read(u),read(v);
        p = lca(u,v);
        if(p<=n) ans = dis[u]+dis[v]-(dis[p]<<1); //编号不大于n的节点,即是圆点
        else{
            A = find(u,p),B = find(v,p); //找到儿子A,B
            ans = dis[u]+dis[v]-dis[A]-dis[B];
            if(sum[A]<sum[B]) swap(A,B); //防止出现负数,这里要swap一下
            ans += min(sum[A]-sum[B],sum[p]+sum[B]-sum[A]);
        }
        print(ans);
        putchar('\n');
    }
    return 0;
}

inline int find(int u,int f){
    int res;
    while(top[u]!=top[f]){
        res = top[u];
        u = fa[top[u]];
    }
    return u==f?res:son[f]; 
}

inline int lca(int u,int v){
    while(top[u]!=top[v]){
        if(dep[top[u]]<dep[top[v]]) swap(u,v);
        u = fa[top[u]];
    }
    return dep[u]<dep[v]?u:v;
}

void dfs1(int u,int f){
    fa[u] = f;
    dep[u] = dep[f]+1;
    size[u] = 1;
    int v,t = -1,l = adj[u].size();
    for(int i=0;i<l;++i){
        v = adj[u][i].v;
        if(v==f) continue;
        dis[v] = dis[u]+adj[u][i].w;
        dfs1(v,u);
        size[u] += size[v];
        if(size[v]>t){
            t = size[v];
            son[u] = v;
        }
    }
}

void dfs2(int u,int f){
    top[u] = f;
    if(son[u]==0) return;
    dfs2(son[u],f);
    int v,l = adj[u].size();
    for(int i=0;i<l;++i){
        v = adj[u][i].v;
        if(v==fa[u]||v==son[u]) continue;
        dfs2(v,v);
    }
}

void tarjan(int u,int f){
    dfn[u] = low[u] = ++cnt;
    int v,w,l = g[u].size();
    for(int i=0;i<l;++i){
        v = g[u][i].v;
        if(v==f) continue; //求点双时不能走到父亲
        w = g[u][i].w;
        if(!dfn[v]){
            fa[v] = u,b[v] = w; //把u->v的边权存到v上
            tarjan(v,u);
            low[u] = min(low[u],low[v]);
        }
        else low[u] = min(low[u],dfn[v]);
        if(low[v]<=dfn[u]) continue;
        //圆点之间的连边,保留原图中数据
        adj[u].push_back(edge(v,w));
        adj[v].push_back(edge(u,w));
    }
    for(int i=0;i<l;++i){
        v = g[u][i].v;
        if(fa[v]==u||dfn[v]<=dfn[u]) continue; 
        //找到非树边,然后建方点并连边
        solve(u,v,g[u][i].w);
    }
}

inline void solve(int u,int v,int w){
    //参数w为非树边的边权
    ++ext;
    int pw,pre = w,i = v;
    while(i!=fa[u]){
        sum[i] = pre;
        pre += b[i];
        i = fa[i];
    }
    sum[ext] = sum[u]; //把整个环的边权和存到方点上
    sum[u] = 0;
    i = v;
    while(i!=fa[u]){
        pw = min(sum[i],sum[ext]-sum[i]);
        //找最短路,建树边
        adj[ext].push_back(edge(i,pw));
        adj[i].push_back(edge(ext,pw));
        i = fa[i];
    }
}

inline int min(int x,int y){
    return x<y?x:y;
}

inline void read(int &x){
    x = 0;
    char c = getchar();
    while(c<'0'||c>'9') c = getchar();
    while(c>='0'&&c<='9'){           
        x = (x<<3)+(x<<1)+(c^48);
        c = getchar();
    }
}

void print(int x){
    if(x>9) print(x/10);
    putchar(x%10+'0');
}