自动搬运

查看原文

来自洛谷，原作者为

	warzone 梦违科学世纪

搬运于2025-08-24 22:08:32，当前版本为作者最后更新于2024-09-09 01:06:31，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

本题给出了无向图上的一种可逆变换，询问无向图是否能从初始状态化为目标状态，
属于 Schreier-Sims 算法 的应用场景。

考虑如何用群论给本题建模。

首先，设 $0$ 号棋子初始位置为 $r$，则任意 “将 $0$ 号棋子从点 $r$ 移动若干步到点 $u$” 的变换总能分解为
先将 $0$ 号棋子移动若干步回到点 $r$，再将 $0$ 号棋子沿一条确定的简单路径移动到点 $u$。
这是显然的。若已将 $0$ 号棋子移动到了点 $u$，总能先将 $0$ 号棋子先沿该简单路径移动回点 $r$
再原路返回 $u$。
这样，问题转化为是否存在目标的 “$0$ 号棋子移动若干步回到点 $r$” 的变换。

“$0$ 号棋子移动若干步回到点 $r$” 的变换显然是关于棋子 $1,2,\cdots,n-1$ 的 $n-1$ 元置换。
若能给出这些变换所构成置换群的一组规模足够小的生成元，
就能使用 Schreier-Sims 算法实现题目要求的判定了。

---

如何给出一组规模足够小的生成元呢？
首先注意到，若 $0$ 号棋子走一条简单回路回到 $r$ 点，
则除点 $r$ 外，环上的所有点发生了一次轮换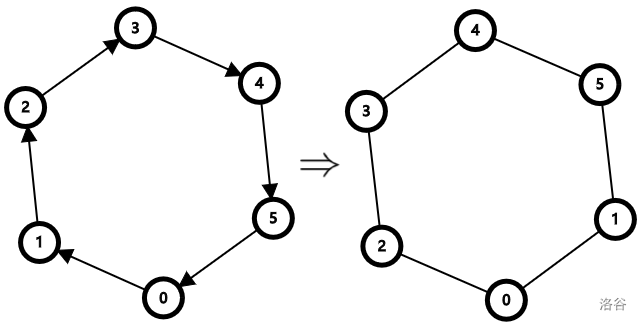

对于一般的回路又如何呢？ 注意到，若 $0$ 号棋子移动若干步后原路返回，
是不会影响当前局面的，因此我们可以作如下分解：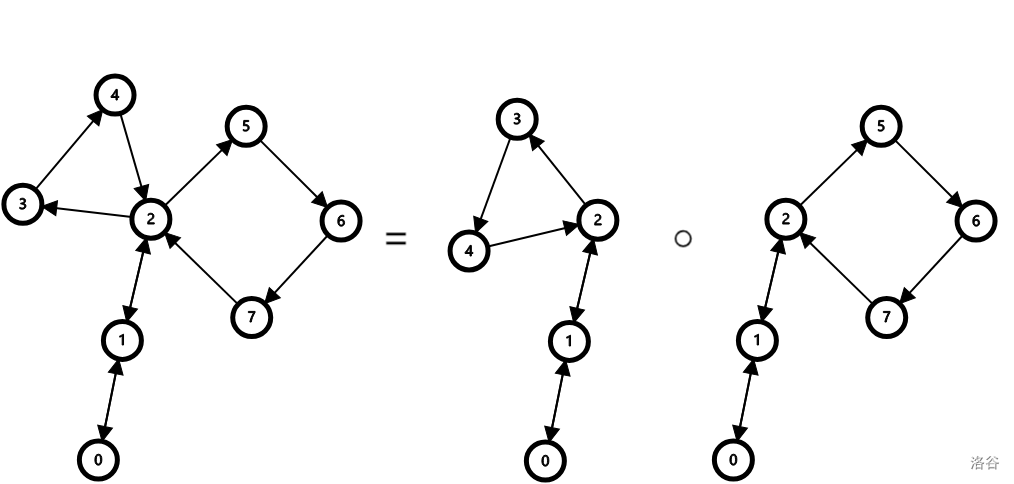

即，通过在合适的时刻沿着已经过的点返回 $r$ 再回去，使得一般的回路总可分解为形如

$$\texttt{一条简单路径 }w\ +\texttt{一个简单环}+\texttt{沿 }w\texttt{ 原路返回 }r $$

的回路，这样的回路只在简单环上发生了一次轮换。

更进一步地，考虑建立题目所给无向图的一棵生成树。
对于以 $r$ 为起点的任意一条回路，设其依次经过的非树边为

$$e_1,e_2,\cdots,e_k$$

每次走到 $e_i\ (i\in[1,k)\cap\N)$ 的终点，先沿树边返回点 $r$，
再前往 $e_{i+1}$ 的起点，显然是不影响回路对当前局面的变换的。
因此，这条回路总可分解为若干与非树边一一对应的回路

$$\texttt{沿树边走到非树边的起点}+\texttt{沿非树边走到非树边的终点}+\texttt{沿树边返回点 }r $$

这些与非树边一一对应的回路就是我们所要找的生成元。这组生成元的规模不超过 $m$。

Code

/*
this code is made by warzone
2024-09-09 01:05
*/
#include<stdio.h>
#include<string.h>
#include<math.h>
#include<vector>
typedef unsigned int word;
struct READ{//快读快写
	char c,w;
	inline READ(){c=getchar();}
	template<typename type>
	inline READ& operator >>(type& num){
		while('0'>c||c>'9') c=getchar();
		for(num=0;'0'<=c&&c<='9';c=getchar())
			num=num*10+(c-'0');
		return *this;
	}
}cin;
word n,m,q;
struct perm{//置换类
	word num[64];
	inline perm(){}
	inline perm(const perm &p)=default;
	inline perm(const perm &p,const perm &q){
		for(word i=0;i<=n;++i)
			num[i]=p.num[q.num[i]];
	}
	inline perm _1()const{
		perm p;
		for(word i=0;i<=n;++i)
			p.num[num[i]]=i;
		return p;
	}
}p,begin;
std::vector<perm> section[64];
word norm[64][64];
inline void insert(perm &p,const word n){
	// Schreier-Sims 算法主体
	word m=n;
	for(;m>1&&norm[m][p.num[m]]!=0xffff'ffff;--m) if(p.num[m]!=m){
		p=perm(section[m][norm[m][p.num[m]]]._1(),p);
		if(p.num[m]!=m) break;
	}
	if(m==1) return;
	const word siz=section[n].size();
	for(word i=0;i<siz;++i){
		word &get=norm[n][p.num[section[n][i].num[n]]];
		if(get==0xffff'ffff){
			get=section[n].size();
			section[n].push_back(perm(p,section[n][i]));
		}
	}
	if(siz==section[n].size()){
		insert(p,n-1);
		for(word i=1;i<siz;++i){
			perm q(p,section[n][i]);
			q=perm(section[n][norm[n][q.num[n]]]._1(),q);
			insert(q,n-1);
		}
		return;
	}
	for(word i=siz;i<section[n].size();++i)
		for(word j=1;j<=n;++j)
			for(word k=1;k<section[j].size();++k){
				word &get=norm[n][section[j][k].num[section[n][i].num[n]]];
				if(get==0xffff'ffff){
					get=section[n].size();
					section[n].push_back(perm(section[j][k],section[n][i]));
				}
			}
	std::vector<perm> add;
	for(word i=siz;i<section[n].size();++i){
		for(word j=1;j<=n;++j)
			for(word k=1;k<section[j].size();++k){
				const perm p(section[j][k],section[n][i]);
				add.push_back(perm(section[n][norm[n][p.num[n]]]._1(),p));
			}
		for(word j=0;j<siz;++j){
			const perm p(section[n][i],section[n][j]);
			add.push_back(perm(section[n][norm[n][p.num[n]]]._1(),p));
		}
	}
	for(auto &p:add) insert(p,n-1);
}
word head[64],to[256],next[256];
#define floor floor_
word fa[64],floor[64],stack[64],top;
bool use[64];
inline void dfs(word id){//建立生成树
	use[id]=1,stack[++top]=id;
	for(word i=head[id];i;i=next[i]) if(use[to[i]]){//非树边，加入生成元
		if(floor[to[i]]>=floor[id]) continue;
		word get=top;
		while(stack[get]!=to[i]) --get;
		if(get==top) continue;
		for(word i=0;i<=n;++i) p.num[i]=i;
		p.num[begin.num[stack[top]]]=begin.num[stack[get+1]];
		for(word k=get+1;k<top;++k)
			p.num[begin.num[stack[k]]]=begin.num[stack[k+1]];
		insert(p,n);
	}else floor[to[i]]=floor[id]+1,fa[to[i]]=id,dfs(to[i]);//树边
	--top;
}
int main(){
	memset(norm,0xff,sizeof(norm));
	cin>>n>>m>>q,--n;
	for(word i=1;i<=m;++i){
		cin>>to[i<<1]>>to[i<<1|1];
		--to[i<<1],--to[i<<1|1];
		next[i<<1]=head[to[i<<1|1]];
		next[i<<1|1]=head[to[i<<1]];
		head[to[i<<1]]=i<<1|1;
		head[to[i<<1|1]]=i<<1;
	}
	word r=0;
	for(word i=0;i<=n;++i)
		if(cin>>begin.num[i],begin.num[i]==0) r=i;
		//此时 begin[i] 为 i 号点的初始棋子编号
		//将 i 号点重标号为为 i 号点的初始棋子编号，则 begin[i] 为原标号 -> 重标号的映射
	for(word i=0;i<=n;++i) p.num[i]=i,norm[i][i]=0;
	for(word i=1;i<=n;++i)
		section[i].push_back(p);
	fa[r]=r,dfs(r),begin=begin._1();//此时 begin 为重标号 -> 原标号的映射
	for(word now;q;--q){
		for(word i=0;i<=n;++i)
			if(cin>>p.num[i],p.num[i]==0) now=i;
		for(;now!=r;now=fa[now])//沿确定的简单路径返回 r
			std::swap(p.num[now],p.num[fa[now]]);
		p=perm(p,begin);
		word m=n;
		for(;m>1&&norm[m][p.num[m]]!=0xffff'ffff;--m) if(p.num[m]!=m){
			p=perm(section[m][norm[m][p.num[m]]]._1(),p);
			if(p.num[m]!=m) break;
		}//使用强生成元完成查询操作
		puts(m==1? "Yes":"No");
	}
	return 0;
}