自动搬运

查看原文

来自洛谷，原作者为

	2017gdgzoi999 哪怕有天，终将分散；相同旅程，也未孤单。 | Even someday, we must depart; in same journey, don't be apart.

搬运于2025-08-24 22:08:28，当前版本为作者最后更新于2019-02-27 13:56:43，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

$2019-03-04$ $update$:增加了一些优化

---

这一题，$O(n^4)$暴力能过，不开$O2$极限数据大概$980ms$，还没有离散化（用了离散化极限数据估计是很快的）。

这个错误的做法是每个人都能凭直觉想到的。

错误做法$1$:对于每个立方体，直接暴力染色。最后枚举所有的相邻的两个块组合，如果其中正好一个染了色一个没有染色（显然他们之间有面积为1的表面），计数器$+1$,如图:

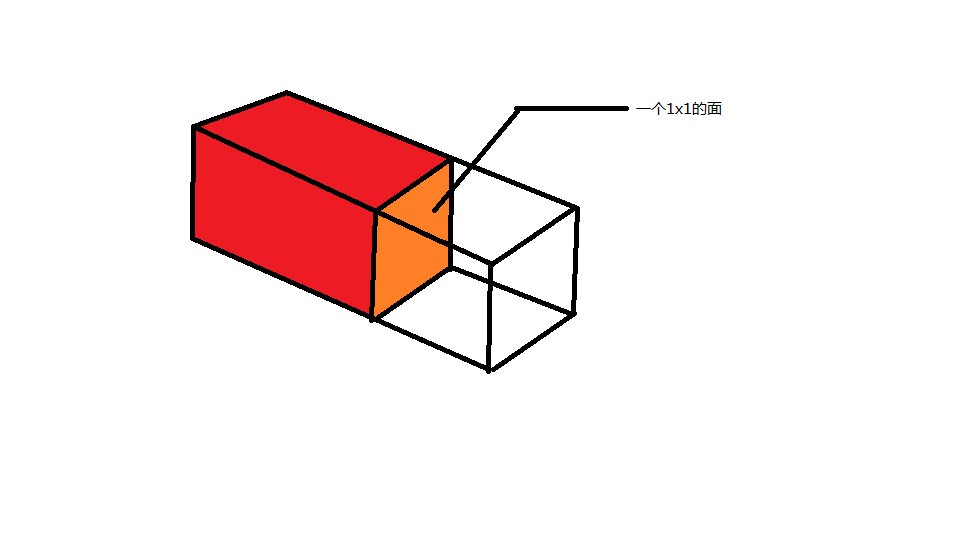
一提交，WA声一片。什么情况？慢着，仔细看题目。

错误原因：题目要你求的是图形的外表面积，如果图形内有空洞，则多余计算，导致答案错误。$\color{gold}55pts$

这下明白了原因了。究竟怎么判断一个面是不是外表面呢？如果你做过这一题，肯定会想到搜索。从$\{0,0,0\}$开始搜索，每一个$x,y,z$都保证在区间$[0, n+1]$之间，被染色的方格设为障碍，每到一个地方打标记。

那么枚举每一个被染色的方格时，旁边六联通有多少个没被染色但是被标记了的方格，计数器就加多少。于是就有了这个方法：

错误做法$2$:对于每个立方体，直接暴力染色。然后按照以上规则进行$DFS$。最后枚举所有的相邻的两个块组合，如果其中正好一个染了色，另外一个一个没有染色并且被标记，计数器$+1$。

错误原因：自己想一下可知$DFS$递归层数最多可以达到$maxn^3$层，会导致$RE$、$MLE$。$\color{orange}36pts$

$DFS$层数太多，会导致爆内存、运行时错误，所以才用占用内存较小的$BFS$。

正确做法$1$:对于每个立方体，直接暴力染色。然后按照以上规则进行$BFS$。最后枚举所有的相邻的两个块组合，如果其中正好一个染了色，另外一个一个没有染色并且被标记，计数器$+1$。

这样就稳A了，贴代码：

#include <iostream>
#include <cstdio>
#include <queue>
#include <algorithm>

#define c(x, xx) ((~x) && (x<=xx)) // 判断是否越出边界
using namespace std;
const int MAXN = 210;

struct data {
	int x, y, z;
};
int a[MAXN][MAXN][MAXN], xx, yy, zz; // 染色/标记状态和地图大小
int gx[6] = {1, -1, 0, 0, 0, 0}; // 存储六联通的六个方向
int gy[6] = {0, 0, 1, -1, 0, 0};
int gz[6] = {0, 0, 0, 0, 1, -1};


void bfs() { // 广搜
	queue<data> q;
	q.push((data) {0, 0, 0}); a[0][0][0] = 2;
	while (!q.empty()) {
		data u = q.front(); q.pop(); // 获得队首
		int x, y, z;
		for (int i=0; i<6; ++i) { // 每局每个方向
			x = u.x+gx[i]; y = u.y+gy[i]; z = u.z+gz[i]; // 获得到达点的坐标
			if (c(x, xx) && c(y, yy) && c(z, zz)) { // 到达点必须不越界
				if (!a[x][y][z]) { // 到达点必须没被染色也没被标记
					a[x][y][z] = 2; q.push((data) {x, y, z}); // 完全满足条件，标记到达点
				}
			}
		}
	}
}
int main() {
	int n; scanf("%d", &n);
	for (int i=1; i<=n; ++i) {
		int x, y, z, x2, y2, z2;
		scanf("%d%d%d%d%d%d", &x, &y, &z, &x2, &y2, &z2);
		++x; ++y; ++z; // 注意左端要加一
		xx = max(xx, max(x, x2)); // 获取地图长宽高
		yy = max(yy, max(y, y2));
		zz = max(zz, max(z, z2));
		for (int i=x; i<=x2; ++i) { // 暴力染色
			for (int j=y; j<=y2; ++j) {
				for (int k=z; k<=z2; ++k) a[i][j][k] = true;
			}
		}
	}
	++xx; ++yy; ++zz; // 因为搜索需要，长宽高各加一
	bfs(); // 广搜
	int res = 0;
	for (int i=1; i<=xx; ++i) { // 枚举每一个格
		for (int j=1; j<=yy; ++j) {
			for (int k=1; k<=zz; ++k) {
				if (a[i][j][k]==1) { // 如果这个各自被染色过
					for (int t=0; t<6; ++t) {
						if (2==a[i+gx[t]][j+gy[t]][k+gz[t]]) ++res; // 如果这个相邻的格子有标记，计数器加一
					}
				}
			}
		}
	}
	printf("%d\n", res);
}

---

$emm$...交上去总时间$1770ms$，最后一个点够猛的，$988ms$，差点就$\color{darkblue}T$了。按照题目上传者的设想，如果时间限制改为$500ms$，不$\color{darkblue}\text{T飞}$才怪！

如果你想要让时间更好看的话，不妨来想如何优化。

首先从最慢的$test$ $11$看：

200
0 0 0 200 200 200
0 0 0 200 200 200
......
0 0 0 200 200 200

看来是个极限数据，必须要卡常才能过。

$but$... 发现有很多重复的方块，优化方法就出来了。

每输入一个方块，检查之前的方块，如果和之前的某个方块重合或被完全包含，则它没有染色的必要 ，忽略这个方块不填充。（应该很容易想到吧）

正确做法$2$：忽略不必要的染色，其余同正确做法$1$。

核心代码：

    for (int i=1; i<=n; ++i) {
        scanf("%d%d%d%d%d%d", &x[i], &y[i], &z[i], &x2[i], &y2[i], &z2[i]);
        ++x[i]; ++y[i]; ++z[i];
    }
    for (int i=1; i<=n; ++i) {
        int x = ::x[i],
        y = ::y[i],
        z = ::z[i],
        x2 = ::x2[i],
        y2 = ::y2[i],
        z2 = ::z2[i];
        bool flag = false;
        for (int j=1; j<i; ++j) { // 检查每一个方块是否不必放置
            if (((::x[j]<=x) && (::x2[j]>=x2)) && ((::y[j]<=y) && (::y2[j]>=y2)) && ((::z[j]<=z) && (::z2[j]>=z2))) {
                flag = true; break;
            }
        }
        if (flag) continue;

总时间下降到$905ms$，大数据很快就被优化到$125ms$，还是比较慢。

---

大数据还是比较慢，原因：$BFS$占用大量时间（$STL$自带大常数）。考虑减少$BFS$所用时间。一种方法是减小地图大小。

继续观察$test$ $11$。

发现所有的数字都是$0$和$200$。

慢！数字只有$2$种！说句正话，研究节省时间的最好方式是......

使用离散化！

于是我们很高兴地敲了离散化，并且在最后统计结果时略作改变。

对于每一个维度，额外加一个数组$delta[]$，统计原本它们之间的长度。这样，外表面积统计时，增加的值是：

$delta[x,i] \times delta[y,j] \times delta[z,k]$

$/ delta[\text{两个位置的方向所代表的值,这个方向代表的循环变量}]$

（太长了于是分两行写）

为节省代码长度，离散化可以封装。

正确做法$3$：在正确做法$2$的基础上，增加离散化并修改计算外表面积方法。

核心代码：

第一个代码：离散化(已封装)

int doit(int a[], int b[], int d[]) { // 将a数组和b数组离散，delta存到d
    int *r = new (int[(MAXN<<1)+3]); // 排序用数组
    int *m = new (int[(MAXN<<1)+3]); // 映射数组
    for (int i=1; i<=n; ++i) {
        r[i] = a[i]; r[n+i] = b[i]; // 初始化排序数组
    }
    sort(r+1, r+(n<<1)+1); r[0] = -1;
    int id = 0;
    for (int i=1; i<=n<<1; ++i) { // 排序后离散化
        if (r[i-1]!=r[i]) d[++id] = r[i]-r[i-1];
        m[r[i]] = id;
    }
    for (int i=1; i<=n; ++i) {
        a[i] = m[a[i]]; b[i] = m[b[i]];
    }
    return id+1;
}

第二个代码：计算外表面积

    int res = 0; // 计算外表面积
    for (int i=1; i<=xx; ++i) {
        for (int j=1; j<=yy; ++j) {
            for (int k=1; k<=zz; ++k) {
                if (a[i][j][k]==1) {
                    for (int t=0; t<6; ++t) {
                        if (2==a[i+gx[t]][j+gy[t]][k+gz[t]]) { // 找到一对组合
                            int tmp = 1; // tmp表示这一对增加的外表面积
                            if (!gx[t]) tmp *= dx[i];
                            if (!gy[t]) tmp *= dy[j];
                            if (!gz[t]) tmp *= dz[k];
                            res += tmp; // 更新结果
                        }
                    }
                }
            }
        }
    }

提交结果：$267ms$，第$11$个数据点仅用了$3ms$。

完整的代码：

#include <iostream>
#include <cstdio>
#include <queue>
#include <algorithm>

#define c(x, xx) ((~x) && (x<=xx))
using namespace std;
const int MAXN = 210;

struct data {
    int x, y, z;
};
int a[MAXN][MAXN][MAXN], xx, yy, zz, n;
int x[MAXN], y[MAXN], z[MAXN], x2[MAXN], y2[MAXN], z2[MAXN];
int dx[MAXN], dy[MAXN], dz[MAXN];
int gx[6] = {1, -1, 0, 0, 0, 0};
int gy[6] = {0, 0, 1, -1, 0, 0};
int gz[6] = {0, 0, 0, 0, 1, -1};

int doit(int a[], int b[], int d[]) {
    int *r = new (int[(MAXN<<1)+3]);
    int *m = new (int[(MAXN<<1)+3]);
    for (int i=1; i<=n; ++i) {
        r[i] = a[i]; r[n+i] = b[i];
    }
    sort(r+1, r+(n<<1)+1); r[0] = -1;
    int id = 0;
    for (int i=1; i<=n<<1; ++i) {
        if (r[i-1]!=r[i]) d[++id] = r[i]-r[i-1];
        m[r[i]] = id;
    }
    for (int i=1; i<=n; ++i) {
        a[i] = m[a[i]]; b[i] = m[b[i]];
    }
    return id+1;
}
void bfs() {
    queue<data> q;
    q.push((data) {0, 0, 0}); a[0][0][0] = 2;
    while (!q.empty()) {
        data u = q.front(); q.pop();
        int x, y, z;
        for (int i=0; i<6; ++i) {
            x = u.x+gx[i]; y = u.y+gy[i]; z = u.z+gz[i];
            if (c(x, xx) && c(y, yy) && c(z, zz)) {
                if (!a[x][y][z]) {
                    a[x][y][z] = 2; q.push((data) {x, y, z});
                }
            }
        }
    }
}
int main() {
    scanf("%d", &n);
    for (int i=1; i<=n; ++i) {
        scanf("%d%d%d%d%d%d", &x[i], &y[i], &z[i], &x2[i], &y2[i], &z2[i]);
    }
    xx = doit(x, x2, dx);
    yy = doit(y, y2, dy);
    zz = doit(z, z2, dz);
    for (int i=1; i<=n; ++i) {
        int x = ::x[i],
        y = ::y[i],
        z = ::z[i],
        x2 = ::x2[i],
        y2 = ::y2[i],
        z2 = ::z2[i];
        bool flag = false;
        for (int j=1; j<i; ++j) {
            if (((::x[j]<=x) && (::x2[j]>=x2)) && ((::y[j]<=y) && (::y2[j]>=y2)) && ((::z[j]<=z) && (::z2[j]>=z2))) {
                flag = true; break;
            }
        }
        if (flag) continue;
        for (int j=x+1; j<=x2; ++j) {
            for (int k=y+1; k<=y2; ++k) {
                for (int l=z+1; l<=z2; ++l) a[j][k][l] = true;
            }
        }
    }
    bfs();
    int res = 0;
    for (int i=1; i<=xx; ++i) {
        for (int j=1; j<=yy; ++j) {
            for (int k=1; k<=zz; ++k) {
                if (a[i][j][k]==1) {
                    for (int t=0; t<6; ++t) {
                        if (2==a[i+gx[t]][j+gy[t]][k+gz[t]]) {
                            int tmp = 1;
                            if (!gx[t]) tmp *= dx[i];
                            if (!gy[t]) tmp *= dy[j];
                            if (!gz[t]) tmp *= dz[k];
                            res += tmp;
                        }
                    }
                }
            }
        }
    }
    printf("%d\n", res);
}

---

当然这些优化在数据相对随机的情况下是比较有用的，当然，一些奇奇怪怪的数据（例如每两个方块都互不包含、重合，且数据包含$0-200$之间的所有数字）要卡卡常。

建议的其它优化方案：

1. 开$O2$优化吸氧（$STL$很有用）；

2. 手写队列（比$STL$快很多，推荐）。

---

总结：

• 细心看好题目。

• 在注意时间限制的同时也要注意空间限制，必要时使用占用空间少的$BFS$。

• 估计自己的算法在不同数据特点下的效率。