自动搬运

查看原文

来自洛谷，原作者为

	joe19025 **

搬运于2025-08-24 22:08:13，当前版本为作者最后更新于2019-02-24 16:04:51，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

Solution

前记

第一次想的时候猜了各种玄学结论，但也没想明白，后来看了官方解法也没太懂，后来仔细推敲后才想明白。

结论

首先我们发现普通边构成一棵树。2条非普通边加树边能形成环，条件如下。

两条非普通边连接树上两点，能成环当且仅当，一对点在树上的路径与另一对点在树上的路径有重合。画个图解释+粗糙证明一下。

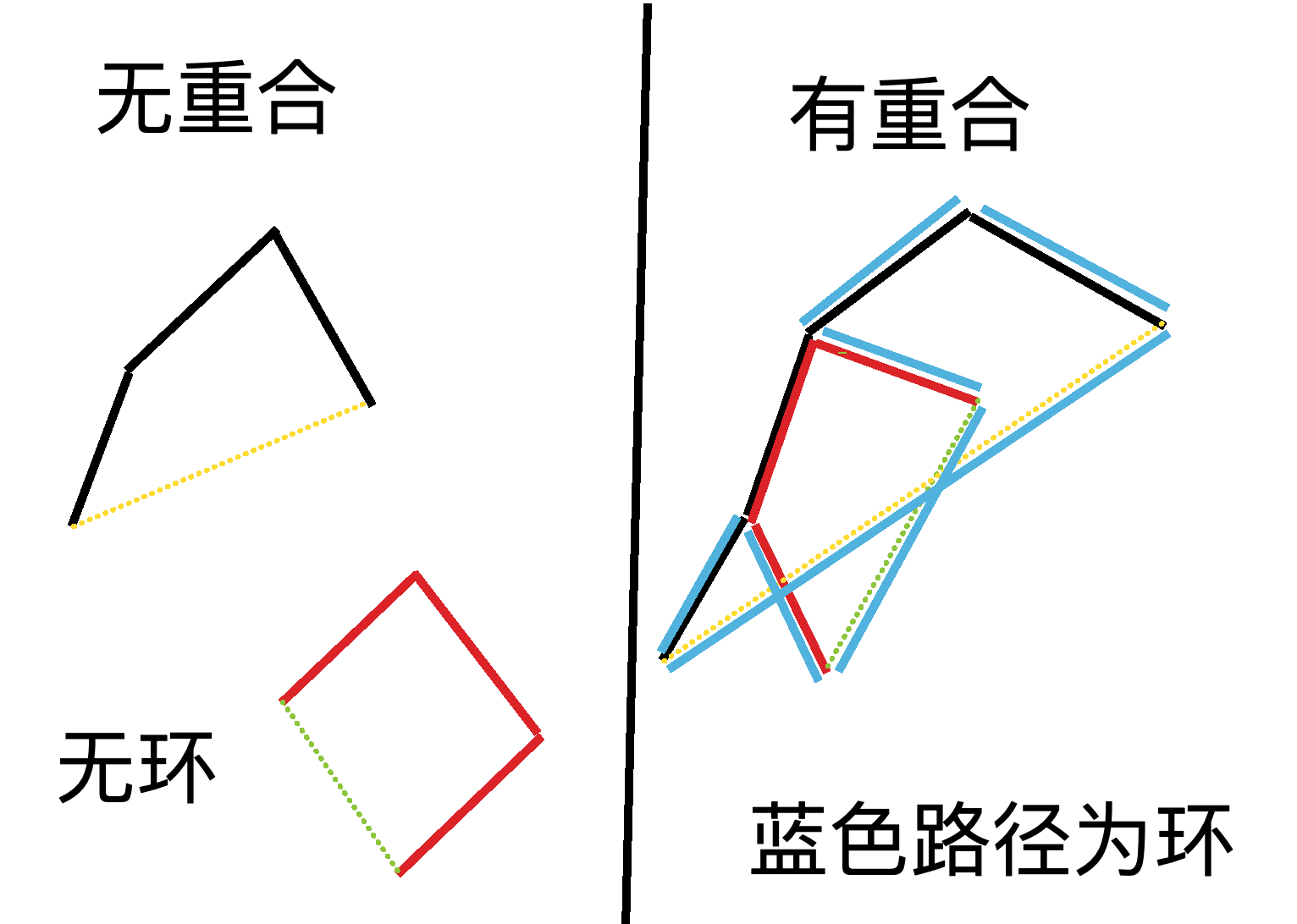
转化

问题变为求有多少个这样的树上路径之间相互重合。

拆路径

把路径拆成两部分，

1. $u->lca(u,v)$
2. $v->lca(u,v)$

这样就变成两条直上直下的路径了，也就好记数了。

计数

我们想在一个序列上，我们如何计算重叠序列的个数。为了避免算重复，我们就计算分别每一条线段，与自己重叠且开始在自己之后的，加起来即可。就是（开始在线段右端点前的）-（开始在线段左端点前的）。

对于树上问题同样可以这样做。我们把每一条边和它向下对应的点绑定在一起。同样用类似的方法，我们计算

（开始在$u/v$的）-（开始在$lca(u,v)$的）。因为从一个点向上有且只有一条路径，所以所有和它重叠的路径，起点都在lca和它本身之间。

去重

1. 如果一个路径与两边的路径分别都相交，那它就会被计算两次。我们需要减掉重复的。方法就是用map，我们记录topx，topy（top就是属于祖先向下的哪一支），如果两个相同，就证明他们是两侧相交。要减去。对于一对(topx,topy),我们要减去$(出现次数)*(出现次数-1)/2$

2. 如果两条直上直下的路径他们开始在同一个点，这一对就会被算两次，相当于$n * n$次，但其实只有

   $n * (n-1)/2$次，所以要减去多余的。

复杂度O(nlogn)

Lca，top都是log复杂度。

Code

#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <cstdlib>
#include <vector>
#include <map>
#define MAXN 200005
using namespace std;

vector<int>G[MAXN];
int n,m,cnt;
int a[MAXN],b[MAXN];
int fa[MAXN][20],dep[MAXN];

void dfs(int u,int father,int depth)
{
    fa[u][0]=father;dep[u]=depth;
    for(int i=1;(1<<i)<=depth;i++)
    {
        fa[u][i]=fa[fa[u][i-1]][i-1];
    }
    for(int i=0;i<G[u].size();i++)
    {
        int v=G[u][i];
        if(v==father)continue;
        dfs(v,u,depth+1);
    }
}

int lca(int u,int v)
{
    if(dep[u]<dep[v])swap(u,v);
    for(int i=18;i>=0;i--)
    {
        if(dep[fa[u][i]]>=dep[v])
        {
            u=fa[u][i];
        }
    }
    if(u==v)return u;
    for(int i=18;i>=0;i--)
    {
        if(fa[u][i]!=fa[v][i])
        {
            u=fa[u][i];
            v=fa[v][i];
        }
    }
    return fa[u][0];
}

int GetTop(int u,int anc)
{
    if(u==anc)return -1;
    for(int i=18;i>=0;i--)
    {
        if(dep[fa[u][i]]>dep[anc])
            u=fa[u][i];
    }
    return u;
}

map<pair<int,int>,int>Q;
int sum[MAXN],siz[MAXN];
long long ans=0;

void dfs2(int u,int father,int cur)
{
    siz[u]=cur;
    for(int i=0;i<G[u].size();i++)
    {
        int v=G[u][i];
        if(v==father)continue;
        dfs2(v,u,cur+sum[v]);
    }
}

int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n-1;i++)
    {
        int x,y;
        scanf("%d%d",&x,&y);
        G[x].push_back(y);
        G[y].push_back(x);
    }
    dfs(1,0,1);
    for(int i=n;i<=m;i++)
    {
        scanf("%d%d",&a[i],&b[i]);
        int anc=lca(a[i],b[i]);
        int topx=GetTop(a[i],anc);
        int topy=GetTop(b[i],anc);
        if(topx!=-1)
        {
            sum[topx]++;
            ans-=sum[topx];
        }
        if(topy!=-1)
        {
            sum[topy]++;
            ans-=sum[topy];
        }
        if(topx!=-1 && topy!=-1)
        {
            if(topx>topy)swap(topx,topy);
            ans-=Q[make_pair(topx,topy)];
            Q[make_pair(topx,topy)]++;
        }
    }
    dfs2(1,1,0);
    for(int i=n;i<=m;i++)
    {
        ans+=siz[a[i]]+siz[b[i]]-2*siz[lca(a[i],b[i])];
    }
    printf("%lld",ans);
    return 0;
}