自动搬运

查看原文

来自洛谷，原作者为

	LiaoYF **

搬运于2025-08-24 22:08:03，当前版本为作者最后更新于2025-06-20 15:10:48，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

做法

我写的详细一点。

每次消除一个区间，很容易让人想到用 $f_{i,j}$ 表示将 $i \sim j$ 这一段消除，所需要添加的弹子数量。转移的时候，想要把 $j$ 消除，要么是将 $j$ 单独添加一些弹子消除，要么与 $i \sim j-1$ 的一些同色弹子合并，再添加一些弹子消除。

但是当我们要将 $j$ 和前面的一些弹子合并消除的时候，没法知道之前还剩下几个同色弹子，就没法知道要添加多少了。如果新增状态表示之前弹子的情况，状态数就炸了。

如果能构造一个状态，使得这次合并在前面与 $j$ 合并的那个弹子的位置就被预料到并且计算了花费，然后在处理 $i \sim j$ 这一段的时候再调用，问题就解决了。

使用 P2135 中的技巧，$f_{i,j,x}$ 表示将 $i \sim j$ 这一段消除，并且未来 $j$ 与后面的 $x$ 个本来就存在的弹子合并消除了，所需要添加的弹子数量。可以写出转移：

1. 直接消除 $j$ 和后面的 $x$ 个：$f_{i,j,x}=f_{i,j-1,0}+\max(0,k-x-1)$。

2. 假设 $c_p=c_j$，将 $j$ 和后面的 $x$ 个与 $p$ 合并：$f_{i,j,x}=f_{i,p,x+1}+f_{p+1,j-1,0}$。

那为什么只需要考虑 $j$ 和后面的弹子合并，不需要考虑 $i \sim j-1$ 的弹子和后面的弹子合并呢？借用一下 2009 集训队论文 徐源盛 《对一类动态规划问题的研究》中的一段话。

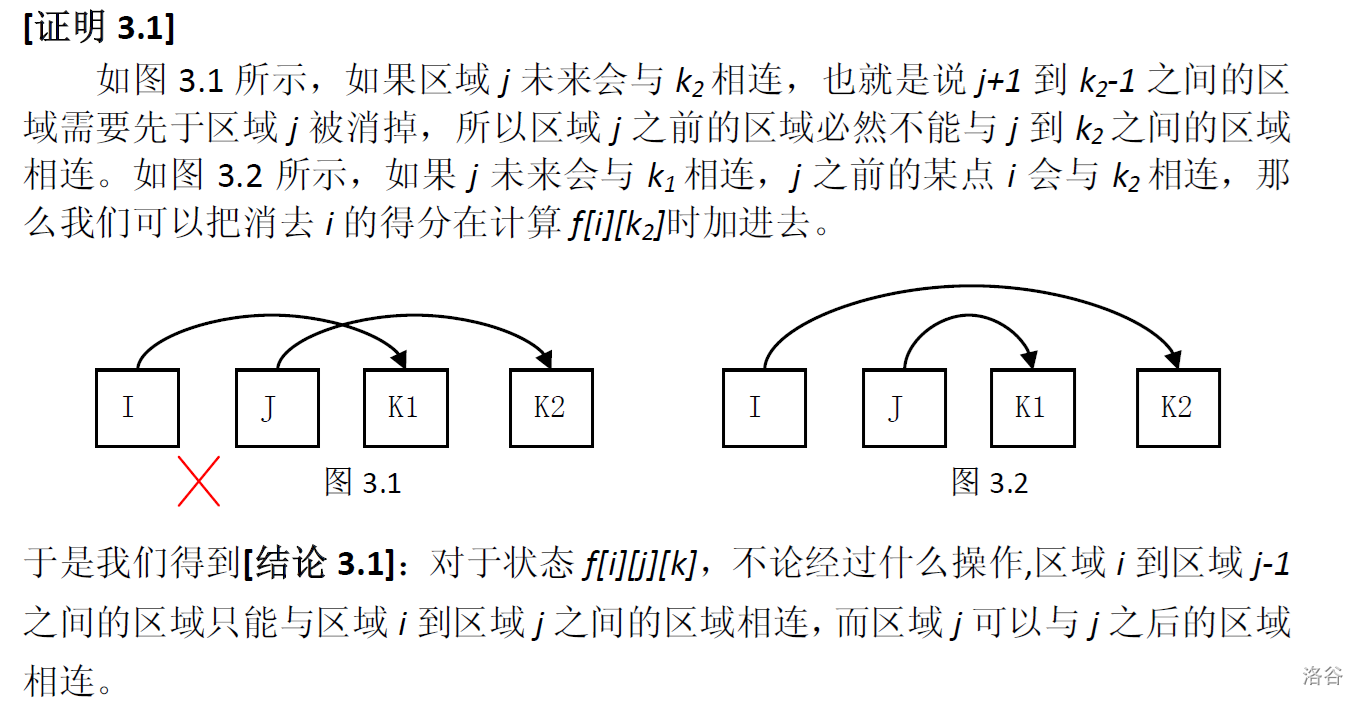
这样已经可以过了，但 $\geq K$ 个弹子合并都不需要额外添加弹子，所以 dp 数组的第三维其实只用算到 $K-1$ 即可。最终时间复杂度 $O(N^3 K)$。

代码

#include<bits/stdc++.h>
#define int long long
#define pii pair<int,int>
#define i128 __int128
#define ALL(x) x.begin(),x.end()
#define popcount(x) __builtin_popcountll(x)
#ifdef LOCAL
#include "debug.h"
#else
#define debug(...) 42
#endif
using namespace std;
const int INF=1e18;
const int N=105;
const int MOD=1e9+7,MOD2=998244353;
int n,k,a[N],f[N][N][6];//和j后面本来就存在的k个一起消除
void solve_(){
    cin>>n>>k;
    for(int i=1;i<=n;i++){
        cin>>a[i];
    }
    for(int len=1;len<=n;len++){
        for(int i=1;i+len-1<=n;i++){
            int j=i+len-1;
            for(int x=0;x<k;x++){
                f[i][j][x]=f[i][j-1][0]+max(0ll,k-x-1);
                for(int p=i;p<j;p++){
                    if(a[p]==a[j]){
                        f[i][j][x]=min(f[i][j][x],f[i][p][min(k-1,x+1)]+f[p+1][j-1][0]);
                    }
                }
            }
        }
    }
    cout<<f[1][n][0]<<"\n";
}
signed main(){
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int testcase,multitest=0;
    if(multitest)cin>>testcase;
    else testcase=1;
    while(testcase--){
        solve_();
    }
    return 0;
}