自动搬运

查看原文

来自洛谷，原作者为

	sukimo Too lazy to write the description

搬运于2025-08-24 22:08:01，当前版本为作者最后更新于2020-09-17 21:43:57，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

看到题目中的滚筒固定宽度，又因为这是经典的一类“刷木条”问题，和长度固定的区间中的最大最小值有关，所以考虑使用单调队列模拟长度为$X$的滚筒，滑动窗口地处理。

问一：处理面积，设木板$i$的高度为$hei_i$，很明显，如果将滚筒置放在$[i,i+X-1]$的区间，它所可以刷到的面积应该是：

$min\left\{hei_j\right\}\times X\ (i\le j\le i+X-1)$

那是不是将每个位置的贡献相加就可以了呢？并非如此，因为贡献可能重复。如何去重？我们设$ok\_rem_i$表示当滑动窗口以$i$为右端点且窗口大小是$X$时（即只有窗口用刷子来刷可以刷下时才统计），窗口内的最小高度。滑动窗口每次向右滑动一位，也就是说每次会有$X-1$个木板重复统计。那么最终结果应该为：

$\sum_{i=x}^n ok\_rem_i\times X-(X-1)\times min\left\{ok\_rem_i,ok\_rem_{i-1}\right\}$

解释一下减号后面的那个东西，即去重。首先上一次重复的宽度是$X-1$，然后重复的高度呢？肯定是这次和上次最小值的最小值，易证。我们把结果设置成最初面积之和，每次减去可刷高度，就是刷不到的。这样我们就解决掉了问一。

问二其实是一种贪心思想，我们假设现在有$w$个高度为$1$的木板，那么最少刷多少次呢？易证：$\lceil{\frac wX}\rceil$次。那么我们算出每一块木板的有效高度（即能刷到的高度，假设为$a$数组），然后对$a$数组进行游程编码，这样就划分出了一些如上面例子中的区间，如样例：

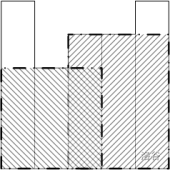
$a:3\ \ \ \ \ 3\ \ \ \ \ 4\ \ \ \ \ 4\ \ \ \ \ 4$ 游程编码：$3\ 2,4\ 3$

因为不同高度的木板肯定不能一次刷，所以只能在相同高度间尽量贪心。那么就把两个区间分别用上面的式子处理，答案就是$\lceil\frac{2}{3}\rceil+\lceil\frac{3}{3}\rceil=2$次。

那么关键就是如何求出$a$数组。以上图的第$3$块木板为例子，它的有效高度与什么有关系呢？$a_3$应等于$max\left\{ok\_rem_3,ok\_rem_4,ok\_rem_5\right\}$，即找若要刷这一块，应以哪块木板做为右端点来刷。由此可以得到：

$a_i=max\left\{ok\_rem_j\right\}(i\le j\le min\left\{n,i+X-1\right\})$

可以发现，这又可以用单调队列$O(n)$地维护，于是问二又解决了。整个问题时间都是$O(n)$。

最后记得开$long\ long$！

$code$：

#include<algorithm>
#include<cstdio>
#include<deque>
#define ll long long
using namespace std;
const int MX=1000005;
ll hei[MX],ok_rem[MX];deque<ll>d;
int main(){
	ll n,m,_min=0,link=1,brush_tot=0;scanf("%lld%lld",&n,&m);
	for(int i=1;i<=n;i++){scanf("%lld",&hei[i]);brush_tot+=hei[i];}
	for(int i=1;i<=n;i++){
		if(!d.empty()&&i-d.front()+1>m)d.pop_front();
		while(!d.empty()&&hei[d.back()]>hei[i])d.pop_back();d.push_back(i);
		if(i>=m){
			ok_rem[i]=hei[d.front()];brush_tot-=hei[d.front()]*m;brush_tot+=min(ok_rem[i-1],hei[d.front()])*(m-1); 
		}
	}
	printf("%lld\n",brush_tot);d.clear();
	for(int i=1;i<=n+m-1;i++){
		if(!d.empty()&&i-d.front()+1>m)d.pop_front();
		if(i<=n){
			while(!d.empty()&&ok_rem[d.back()]<ok_rem[i])d.pop_back();d.push_back(i);
		}
		if(i>=m)hei[i-m+1]=ok_rem[d.front()];
	}
	//下方为游程编码区间公式处理 
	for(int i=2;i<=n;i++)if(hei[i]!=hei[i-1]){_min+=(link+m-1)/m;link=1;}else link++;
	_min+=(link+m-1)/m;printf("%lld",_min);
	return 0;
}
/*
代码中省略掉了a数组，转而直接在ok_rem里面覆盖 
*/