自动搬运

查看原文

来自洛谷，原作者为

	Danno0v0 我们会再次见面的，相信我。再见。

搬运于2025-08-24 22:07:26，当前版本为作者最后更新于2021-11-12 20:17:21，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

真是很有意思的一道题呢 虽然我交了一页才过

首先呢看到 $n \leq 300000$ ，那么枚举每条路径是肯定要 T 飞的。

那么既然是计算期望路径长，不能枚举每条路径，那就把路径拆开，我们来依次枚举每条边会被经过多少次。

还有为了方便，我们可以先算出总路径长再除以方案总数来算期望长度。

有了这些就可以开干了。

题上说有 $n$ 个点 $n$ 条边，那就是基环树，那我们就把在环边和非环边分开来看。

• 非环边

非环边的经过次数应该很好算，次数这条边两侧的点数量之积再乘以 $2$ 。为什么呢，假如这条边一侧有 $a$ 个点，另一侧是有 $b$ 个点，那么如果要经过这条边，那就是要从一侧到另一侧去（假如起点和终点都在同一侧的话那为什么还要经过这条边呢）所以一共有 $a\times b$ 条路径是要经过这条边的，然后又因为假如把起点和终点对调是算两条路径的所以要乘个 $2$ 。

那么非环边对答案的贡献就是 $sum_{left} \times sum_{right} \times 2 \times w_i$ 。

• 环边

首先我们要明白一个道理：假如一条路径经过了环上任意一点，那么一定是存在另一条路径的。

（这也是这道题一个大坑：假设我们要从 $4$ 到 $1$ ，那么其实是有两条路的：

）

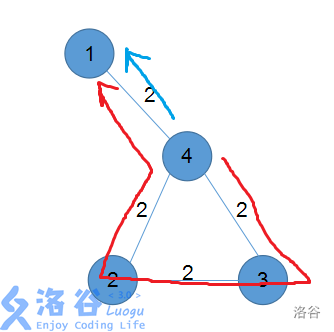
那么这两条路径的长度分别是：

（假设起点是 $a$ 终点是 $b$）

• $a$ 到环的距离 $+$ 环的一侧的长度 $+$ $b$ 到环的距离

• $a$ 到环的距离 $+$ 环的另一侧的长度 $+$ $b$ 到环的距离

它们一起对答案的贡献是：（由于在 $a$ 到 $b$ 的方案中，两条路径的被选择概率都是 $\frac{1}{2}$ ，所以要除一个 $2$）

$(2 \times$ $a$ 到环的距离 $+$ 环的长度 $+$ $2\times b$ 到环的距离$) \div 2$

而我们这里只关注环边的贡献，那么环边的贡献也就是：

环的长度 $\div 2$

那么我们可以推测出：假设有一个起点和终点之间的路径会经过环，那么环边一定会贡献环的长度 $\div 2$ 的贡献。

那么我们就可以算出到底有多少种方案会经过环，再把方案数乘上这个贡献，就是环边的所有贡献了。这里呢先算有多少种方案不经过环再从总方案里扣除比较好算，而一个方案不经过环，那么起点和终点一定满足：

在同一棵子树内；

公共祖先不在环上。

说的简单明了，就是起点和终点一定要在环上的点的同一棵子树内：（如果在环上的点的两颗子树内，那么一定会经过环上的那个点）

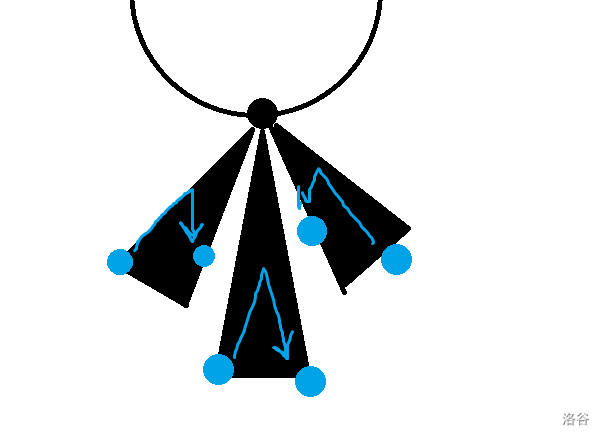
那么，同一棵子树里的点两两之间可以产出一条不经过环的路径，那么总路径就是 $x^2$ 条 ,其中 $x$ 是子树大小；

那么有多少条路径不经过环也就可以算了，也就是所有子树的大小平方之和：

$x_1^2+x_2^2+ \dots x_n^2$

那么有多少条路径经过环也就可以算了，那么环边做出的总贡献也就可以算了：（$length$ 是环的长度）

$length\times(n^2-\sum\limits_{i=1}^nx_i^2)$

然后两种边的贡献就算完了，加起来再除以方案总数，完——

code：

#include<bits/stdc++.h>
#define int long long
using namespace std;
int fi[10000001],nx[10000001],to[10000001],co[10000001],tot,length;
int n;
int loop[10000001],num,size[10000001];
int size_tree;
bool check[10000001],in[10000001],huan;
long long all;
stack<pair<int,int> >sta;
namespace Mod {
    const int mod = 19260817;
    int add(int x, int y) {
        return (x += y) < mod ? x < 0 ? x + mod : x : x - mod;
    }
    int Add(int&x, int y) {
        return (x += y) < mod ? x < 0 ? (x += mod) : x : (x -= mod);
    }
    int mul(int x, int y) {
        return 1LL * x * y % mod;
    }
    int Mul(int&x, int y) {
        return x = 1LL * x * y % mod;
    }
    int qpow(int x, int y) {
        int res = 1;
        for (; y; y >>= 1) {
            if (y & 1) Mul(res, x);
            Mul(x, x);
        }
        return res;
    }
    int inv(int x) {
        return qpow(x, mod - 2);
    }
}
using namespace Mod;
void link(int a,int b,int c)
{
	nx[++tot]=fi[a];
	fi[a]=tot;
	to[tot]=b;
	co[tot]=c;
} 
void dfs1(int now,int fa,int w)
{
	if(in[now])
	{
		length+=w;
		while(sta.top().first!=now)
		{
			loop[++num]=sta.top().first;
			length+=sta.top().second;
			check[sta.top().first]=1;
			sta.pop();
		}
		loop[++num]=now;
		check[now]=1;
		huan=1;
		return;
	}
	sta.push({now,w});
	in[now]=1;
	for(int i=fi[now];i;i=nx[i])
	{
		int v=to[i];
		if(v!=fa)
		{
			dfs1(v,now,co[i]);
			if(huan)
			{
				return;
			}
		}
	}
	sta.pop();
}
void dfs2(int now,int fa,int w)
{
	size[now]=1;
	for(int i=fi[now];i;i=nx[i])
	{
		int v=to[i];
		if(check[v]||v==fa)
		{
			continue;
		}
		dfs2(v,now,co[i]);
		size[now]+=size[v];
		if(check[now])
		{
			Add(size_tree,mul(size[v],size[v]));
		}
	}
	Add(all,mul(w,mul(2,mul(size[now],n-size[now]))));
}
signed main()
{
	cin>>n;
	for(int i=1;i<=n;i++)
	{
		int x,y,z;
		cin>>x>>y>>z;
		link(x,y,z);
		link(y,x,z);
	}
	dfs1(1,0,0);
	for(int i=1;i<=num;i++)
	{
		dfs2(loop[i],0,0);
	}		
	Add(all,mul(mul(add(mul(n,n),-size_tree),length),inv(2)));
	cout<<mul(all,inv(mul(n,n)))<<endl;
}