自动搬运

查看原文

来自洛谷，原作者为

	linyinuo2008 **

搬运于2025-08-24 22:07:24，当前版本为作者最后更新于2021-05-15 15:24:30，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

原题链接

这是一道非常棒的线性动归题，其中还有一些操作小技巧。

1、题意理解

简化版题意：给你 $n$ 个数，让你把这 $n$ 个数分成任意组，每组中包含任意连续不超过 $k$ 个数。当一个数被分到一组中后，它会变成这组数中最大的那个，求分完后这些数和的可能最大值。

例:

5 3
1
2
4
6
1

我们把 $1$, $2$, $4$ 放一组，把 $6$ 和 $2$放一组，得到最大值为 $4 \times 3 + 6 \times 2 = 24$。

通过这个例子，应该已经理解了题意，下面就是一些要点。

• 我们要分的是这 $n$ 头奶牛，并且每组必须是连续的不超过 $k$ 头奶牛。

• 一只奶牛只能属于一组，可以理解为在奶牛序列中放上几块隔板。

2、动态规划求解答案

这题一看就是动态规划，并且符合无后效性的性质（标签上不是写着呢吗）。这里我摘录一段来自这篇博客的解释：

无后效性，有两层含义，第一层含义是，在推导后面阶段状态的时候，我们只关心前面阶段的状态值，不关心这个状态是怎么一步步推导出来的。第二层含义是，某阶段状态一旦确定，就不受之后阶段的决策影响。无后效性是一个非常“宽松”的要求。

所以动归状态很自然的就出来了。我们设 $f_i$ 表示前 $i$ 头奶牛最大的技能水平和，那么我们来研究一下 $f_i$ 可以从哪里转移过来。我们对每一只奶牛进来后最重要的是什么？是把它放在哪一组！我们要确定它的组别。

---

来个栗子。

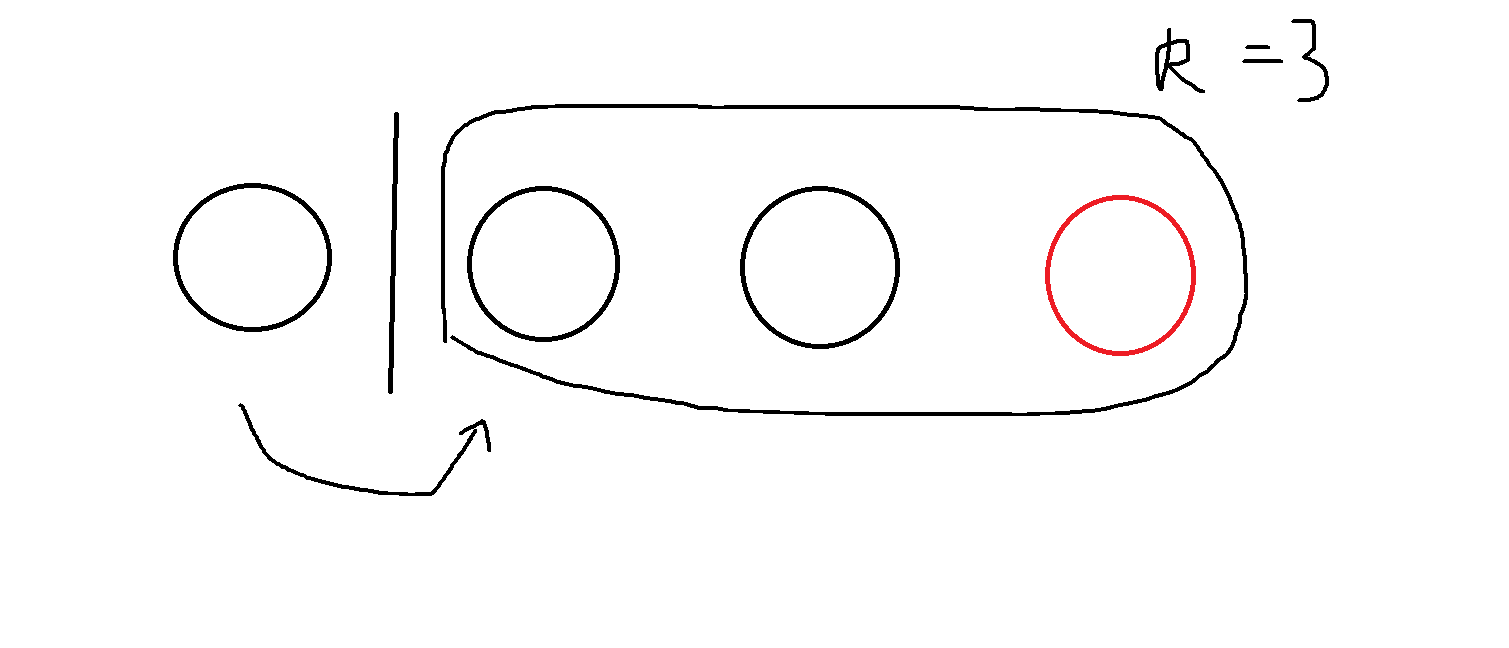
如图，当 $k=3$ 时：

新进来了一头红牛，编号为 $i$，我们把它放哪？

由于一组最多只能放三头，所以我们有三种方法：

把它单独放一组，这种方案是从 $f_{i-1}$ 转移过来的。

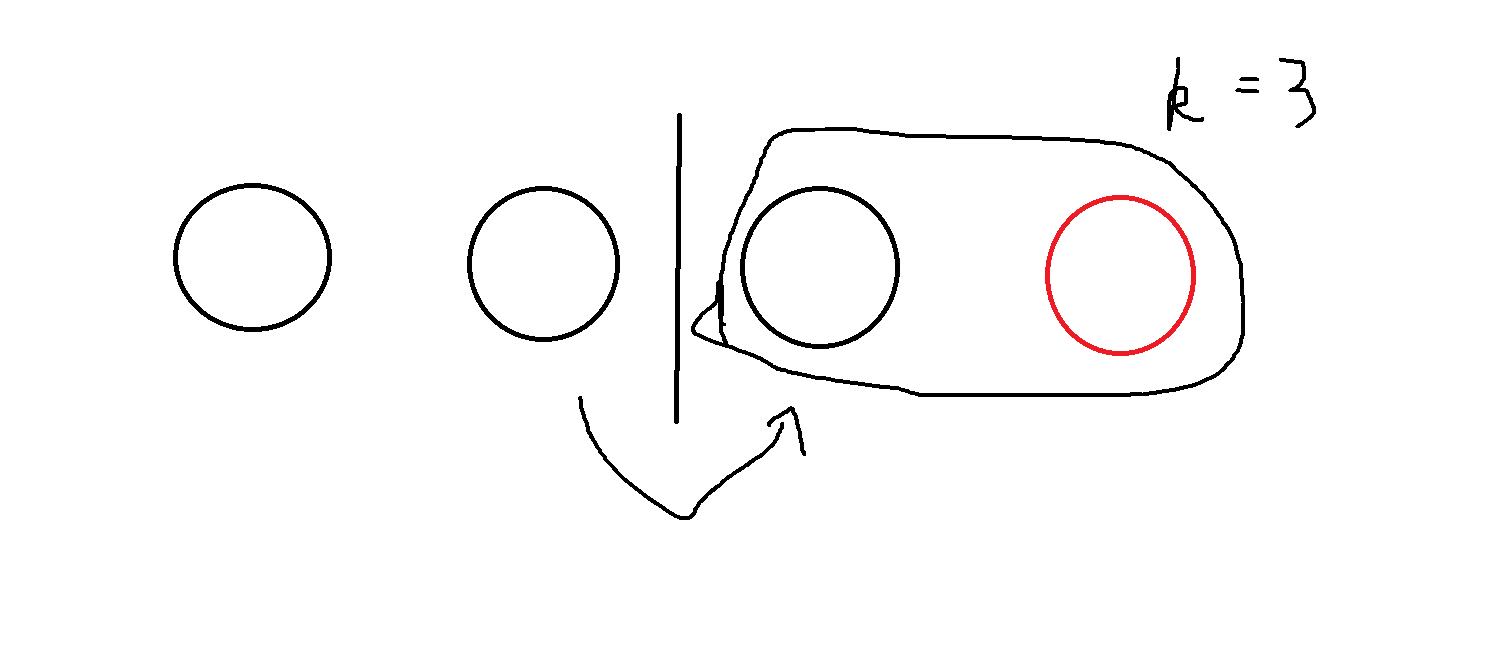
把它和前一只奶牛放一组，这种状态是从 $f_{i-2}$ 转移过来的。

把它和前两只奶牛放一组，这种状态是从 $f_{i-3}$ 转移过来的。

至此，我们就完成了这只奶牛的全部状态转移，并且无法再找到新的状态，因为再往前分组就会超出 $k$ 的约束范围。

---

所以我们的最终 $f_i$ 是什么呢? 显然是从之前的 $f_{j-1}$ 转移过来的，把 $[j,i]$ 这个区间中的奶牛分为一组。但是我们别忘了还要加上这一组的效率和。这里的效率和为为 $mx \times (i-j+1)$ ，其中 $mx$ 为区间 $[j,i]$ 的最大值，意思就是这一组的效率值为这一组中的最大值乘上这一组的组员个数。

但是 $j$ 又要满足什么要求呢？显然，我们选的那一组奶牛数不能超过 $k$ ，也就是说 $[j,i]$ 这个区间长度不能超过 $k$ ，所以 $i-k+1 \leq j \leq i$ ，但这还不够，因为最初 $i-k+1$ 可能为负数，所以左端点还要跟一取最大值，也就是说 $\max(i-k+1,1) \leq j \leq i$。

于是我们就有了这样的代码：

#include <iostream>
using namespace std;
const int N=10005;
int n,k,s[N];
int f[N];
inline int max(int a,int b)
{
	return a>b?a:b;
}
int mx(int k,int l)//在[k,l]区间内取最大值
{
	int maxx=-1;
	for(int i=k;i<=l;i++) maxx=max(maxx,s[i]);		
	return maxx;
}
int main()
{
	cin>>n>>k;
	for(int i=1;i<=n;i++)
		cin>>s[i];
	f[1]=s[1];
	for(int i=2;i<=n;i++)
	{
		for(int j=max(i-k+1,1);j<=i;j++)
		{
			f[i]=max(f[i],f[j-1]+mx(j,i)*(i-j+1));//转移
		}
	}
	cout<<f[n];
    return 0;
}

交上去一看，TLE $\times$ 3。

这是为什么呢？是在这里出了问题：

int mx(int k,int l)//在[k,l]区间内取最大值
{
	int maxx=-1;
	for(int i=k;i<=l;i++) maxx=max(maxx,s[i]);
	return maxx;
}

这里求区间最大值的时间是 $O(n)$ 的，这样一来总复杂度是 $O(n^3)$ ，就炸掉了。所以我们不能在求最大值上花复杂度，所以我们可以每次从 $i$ 倒着枚举到 $\max(i-k+1,1)$ 每次在转移 $f_i$ 时顺便就实现了求 $[j,i]$ 的最大值。

3、AC代码

代码中有注释。

#include <iostream>
using namespace std;
const int N=10005;
int n,k,s[N];
int f[N];
/*
f[i]表示前i头奶牛最大水平和
f[i]=max(f[i],f[j-1]+mx(j,i)*(i-j+1))  (i-k+1<=j<=i) 
*/
int max(int a,int b)
{
	return a>b?a:b;
}
int main()
{
	cin>>n>>k;
	for(int i=1;i<=n;i++)
		cin>>s[i];
	f[1]=s[1];//初始化f[1]=s[1]
	for(int i=2;i<=n;i++)
	{
		int mx=-1;//先设为-1，因为都是正数
		for(int j=i;j>=max(i-k+1,1);j--)//边界条件
		{
			mx=max(mx,s[j]);//先得把mx更新了
			f[i]=max(f[i],f[j-1]+mx*(i-j+1));//才能转移
		}
	}
	cout<<f[n];
    return 0;
}

若有错误，欢迎指出！