自动搬运

查看原文

来自洛谷，原作者为

	GNAQ Good:bye

搬运于2025-08-24 22:06:39，当前版本为作者最后更新于2018-12-16 07:34:52，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

（时间：2020年5月21日 17点58分）

UPD: 论如何气活一个退役选手

最近总是有人说这代码 WA=0 , 我只能说，嗯，有道理。

我当时直接从某个OJ的提交记录里把代码复制了过来，所以这个算法是对的，这点毫无疑问，但是输出格式在谷上会WA

代码我不想改了，保留它本来的样子吧。

---

果然有模板了，那可不能少了我这篇讲解啊

我就不信你理解不了一篇全是图的讲解

后面附赠两道例题练习，也有写好的题解

（本文首发于 「头插DP指北」 ，原博客阅读效果更佳，欢迎围观。）

---

本文概览

• 什么是插头DP

• 插头DP的大致思路

  • 划分阶段

  • 记录状态

  • 转移状态

    • 新建一个连通分量

    • 合并两个连通分量

    • 保持原来的连通分量

    • 一个小优化

• 代码

• 练习题

---

插头DP的概念（据我不可靠考证）最早出现在08年CDQ的论文中，而此类题目早在04年前后就已经存在。

（下面假设聚聚们都会了状压DP……）

1.什么是插头DP

插头DP (PlugDP)，也就是一类基于连通性的状态压缩动态规划，是用状压DP处理联通问题的强劲武器。

常见的类型有棋盘插头DP和CDQ论文里的两个非棋盘上的模型。

常见的联通问题：多回路问题、路径问题、简单回路问题、广义路径问题、生成树问题

2.插头DP的大致思路

2.1 划分阶段

大家都知道了这是基于联通性的状压 DP ，所以本质上还是状压 DP 。

一般设 $\text{dp}[i][j][\mathrm{state}]$ 为 $(i,j)$ 位置，状态为 $\mathrm{state}$ 的方案数（或者代价，等等让你求的东西……）

所以我们状压什么呢？轮廓线。

DP求解棋盘问题是逐格转移的。所以已经转移过的格子和没转移过的格子被一个折线分成了两半儿。这个折线就是轮廓线。

（@远航之曲 的简洁解释:已决策格子和未决策格子的分界线）

就这个蓝线（现在转移的格子是第3行第3个）。

插头又是什么呢？一个格子有四个插头，一个存在的插头表示在它代表的方向上能与相邻的格子连接（联通）。不存在就不能。

为什么要引入插头？要求一个回路，也就意味着最后所有的非障碍格子通过插头连接成了一个连通块，因此转移时需要记录格子的连通情况。

我们递推的时候就是依据轮廓线上的插头存在性，求出所有能转移到的合法状态。

显然回路问题中一个格子恰好有两个插头，一个是 “进来” 的一个是 “出去” 的。

2.2 记录状态

最小表示法：

所有的障碍格子标记为 $0$ ，第一个非障碍格子以及与它连通的所有格子标记为 $1$ ，然后再找第一个未标记的非障碍格子以及与它连通的格子标记为 $2$

……重复这个过程，直到所有的格子都标记完毕。

比如连通信息 $((1,2,5),(3,6),(4))$ 表示为 $\{ 1,1,2,3,1,2 \}$ 。

（还有一种极不常用的最小表示法，即一个连通块内所有的格子都标记成该连通块最左边格子的列编号。）

括号表示法：

【性质】轮廓线上从左到右 $4$ 个插头 $a, b, c, d$ ，如果 $a, c$ 连通，并且与 $b$ 不连通，那么 $b, d$ 一定不连通。**这个性质对所有的棋盘模型的问题都适用。 **(证明详见CDQ论文。)

“两两匹配”，“不会交叉”这样的性质，我们很容易联想到括号匹配。

将轮廓线上每一个连通分量中左边那个插头标记为左括号，右边那个插头标记为右括号，由于插头之间不会交叉，那么左括号一定可以与右括号一一对应，这样我们就可以使用 $3$ 进制， $0$ 表示无插头， $1$ 表示左括号插头， $2$ 表示右括号插头，记录下所有的轮廓线信息。不妨用 $\#$ 表示无插头，那么上面的三幅图分别对应的是 $(())\#(),(()\#)(),(()\#\#\#)$ ，即 $(1122012),(1120212),(1120002)$ ，这种表示方法称为括号表示法。

状态的编码：

对于最小表示法，编码最简单的方法就是表示成一个 $n+1$ 位的 $p$ 进制数， $p$ 可以取能够达到的最大的连通块标号 $+1$。在不会超过数据类型的范围的前提下，建议将 $p$ 改成 $2$ 的幂，因为位运算比普通的运算要快很多。

如需大范围修改连通块标号，最好将状态 $O(n)$ 解码到一个数组中，修改后再 $O(n)$ 计算出新的 $p$ 进制数，而对于只需要局部修改几个标号的情况下，可以直接用 $(x \;\mathrm{div}\; p^{i-1} ) \;\mathrm{mod}\; p$ 来获取第 $i$ 位的状态，然后 $+k \times p^{i-1}$ 直接对第 $i$ 位进行修改。

2.3 转移状态

首先，因为逐行递推要讨论的情况还是比较难处理的，除非要求解的问题特别适合这样做，要不然我们一般使用逐格递推，这样可以方便讨论情况。

一般来说轮廓线上有不少状态都是无用的，而且一般来说头插插头 DP 的状态数很多，所以我们使用一个技巧来加速，那就是，我们用一个线性数据结构（我愿意开一个/模拟一个 vector ）来存储状态，每次读取上一格的所有合法状态扩展，而不是xjb枚举状态来扩展。

然后，我们来研究一下怎么转移。我们看一种题型吧。

(其实就是这道题)

• 给你一个 $m \times n$ 的棋盘，有的格子是障碍，问共有多少条回路使得经过每个非障碍格子恰好一次。

• $m, n \leqslant 12$ 。

• 

---

1.新建一个连通分量

这个情况只出现在转移位置的轮廓线上没有下插头和右插头。

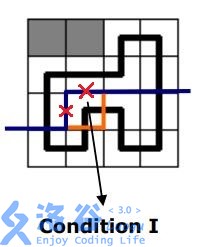
如图。然后我们只有一种转移方式就是当前格做右插头和下插头。

括号表示法就是新建一对紧挨着的左右括号。最小表示法就直接解码重编一下。

2.合并两个连通分量

如果当前轮廓线上既有右插又有下插，那你只能当前格做左插和上插，要不然就不是回路了。

然后如果右插和下插联通，那这种情况只能是在最后一个非障碍格是合法的。

不连通的话，当然这样做会把他们变联通，看图：

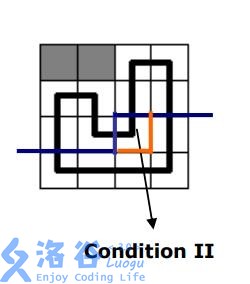
括号表示法里就直接删一对括号，最小表示法还是解码重编。

3.保持原来的连通分量

当轮廓线上只有下插或者右插，就只能当前格做一个左插/上插来满足回路性质，剩下一个插头是随便安排的。

图：

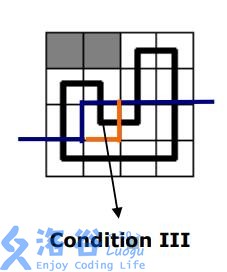
括号表示法的话就把下插/右插对应的括号移到你加的插头上就行了。

最小表示法也类似，把下插/右插位置的记号移到你加的插头对应位置就行（因为是延续了一个连通分量）。

注意当从一行的最后一个格子转移到下一行的第一个格子的时候，轮廓线需要特殊处理。这个看代码最好解释了。

（还要多啰嗦一句，一般状态编码的左右和轮廓线的左右是反着对应的……也就是编码最右面一位是对应轮廓线最左面格子）

( 这样大概比较好写? )

一个小优化

有时候你转移的时候有可能从两个不同状态转移出同一个状态，这个时候我们用 hash 优化它就好了。 hash 表的实现用挂表法就行。

还有提取每个插头状态的时候我们可以预处理一个对应 bit 的数组，然后用上文提到的解码方式去解码。

然后我们就讨论完了插头DP的第一道入门题该怎么做。上代码。这里由于洛谷排版的原因，解释我压在代码下面了，一定要好好看。后面一堆图，我就不信你看不明白是怎么转移的（不过最好的方法是去博客看原文）

• state 是表示状态，dp 表示方案数。这里用了滚动数组来优化空间（ pre , cnt 来滚动）

• bits 是一个方便提取插头的数组。比如 bits[3]=6，那提取第三个格子上面和左面的插头（分别叫做 is_d 和 is_r ）就是 state>>bits[3-1] 和 state>>bits[3]

• 我们存储状态是四进制，括号表示法。 $1$ 表示 $($ ， $2$ 表示 $)$ 。

• hash 表的内部实现你可以看到就是一个链表。( struct hash_table )

• 因为可能最后一格也有障碍，所以要记录一下最后一个无障碍格子( endx , endy )

#include<cstdio>
#include<iostream>
#include<cstring>
#include<string>
#include<cmath>
#include<algorithm>
#include<iterator>
#include<cstdlib>
#include<vector>
#include<queue>
#include<map>
#include<set>
#define ll long long
#define mo 590027
using namespace std;

int n,m,mapx[20][20]={0},endx,endy;
ll all_ans=0,dp[2][600000]={0};

int bits[28]={0};

int state[2][600000]={0},tots[2]={0};
int pre=1,cnt=0;

struct hash_table
{
  int pre,to;
}idx[600000]={0};
int ptr[600000]={0},at=0;

//------------FUNCTIONS HERE------------------------

inline void readx(int& x)
{
  x=0; int k=1; register char ch=0;
  while (ch<'0' || ch>'9') { ch=getchar(); if (ch=='-') k=-1; }
  while (ch>='0' && ch<='9') {x=x*10+ch-'0'; ch=getchar(); }
  x*=k;
}
inline void readit()
{
  readx(n); readx(m);
  char cht=0;
  for (int i=1;i<=n;i++)
    for (int j=1;j<=m;j++)
    {
      cht=0; while (cht!='.' && cht!='*') cht=getchar();
      if (cht=='.') { mapx[i][j]=1; endx=i; endy=j; }
    }
}
inline void init_bits() { for (int i=1;i<=25;i++) bits[i]=(i<<1); }

inline void hah(int sta,ll val)
{
  int key=sta%mo;
  for (int prex=ptr[key];prex;prex=idx[prex].pre) if (state[cnt][idx[prex].to]==sta)
  {
    dp[cnt][idx[prex].to]+=val;
    return;
  }
  tots[cnt]++;
  state[cnt][tots[cnt]]=sta;
  dp[cnt][tots[cnt]]=val;
  
  idx[++at].pre=ptr[key];
  idx[at].to=tots[cnt];
  ptr[key]=at;
}

inline void DP()
{
  tots[cnt]=1; dp[cnt][1]=1;
  state[cnt][1]=0;
  
  for (int i=1;i<=n;i++)
  {
    for (int j=1;j<=tots[cnt];j++) state[cnt][j]<<=2;//!!!
    
    for (int j=1;j<=m;j++)
    {
      at=0; memset(ptr,0,sizeof ptr);//clear hash_table
      swap(pre,cnt);//rolling
      tots[cnt]=0;//clear state counter
      
      register int nowsta,is_d,is_r; register ll nowans;
      for (int k=1;k<=tots[pre];k++)
      {
        nowsta=state[pre][k],nowans=dp[pre][k];//get previous state&answer
        is_d=(nowsta>>bits[j])%4,is_r=(nowsta>>bits[j-1])%4;//get current plugs
        
        if (!mapx[i][j])//case 0
        {
          if ((!is_d) && (!is_r)) hah(nowsta,nowans);
        }
          
        else if ((!is_d) && (!is_r))//case 1
        {
          if (mapx[i+1][j] && mapx[i][j+1])
            hah(nowsta+(1<<bits[j-1])+2*(1<<bits[j]),nowans);
        }
            
        else if ((!is_d) && is_r)//case 2
        {
          if (mapx[i+1][j]) hah(nowsta,nowans);//go down
          if (mapx[i][j+1]) hah(nowsta-is_r*(1<<bits[j-1])+is_r*(1<<bits[j]),nowans);//go right
        }
        
        else if (is_d && (!is_r))//case 3
        {
          if (mapx[i][j+1]) hah(nowsta,nowans);//go right
          if (mapx[i+1][j]) hah(nowsta-is_d*(1<<bits[j])+is_d*(1<<bits[j-1]),nowans);//go down
        }
        
        else if (is_d==1 && is_r==1)//case 4
        {
          register int count=1;
          for (int l=j+1;l<=m;l++)
          {
            if ((nowsta>>bits[l])%4==1) count++;
            else if ((nowsta>>bits[l])%4==2) count--;
            if (!count)
            {
              hah(nowsta-(1<<bits[l])-(1<<bits[j])-(1<<bits[j-1]),nowans);
              break;
            }
          }
        }
        
        else if (is_d==2 && is_r==2)//case 5
        {
          register int count=1;
          for (int l=j-2;l>=0;l--)
          {
            if ((nowsta>>bits[l])%4==1) count--;
            else if ((nowsta>>bits[l])%4==2) count++;
            if (!count)
            {
              hah(nowsta-2*(1<<bits[j])-2*(1<<bits[j-1])+(1<<bits[l]),nowans);
              break;
            }
          }
        }
        
        else if (is_d==1 && is_r==2)//case 6
          hah(nowsta-2*(1<<bits[j-1])-(1<<bits[j]),nowans);
        
        else if (is_r==1 && is_d==2)//case 7
          if (i==endx && j==endy) all_ans+=(ll)nowans;
      }
    }
  }
}

int main()
{
  readit(); init_bits();
  DP();
  printf("%I64d\n",all_ans);
  return 0;
}

• case 0:有障碍。

• case 1:

• case 2:

• case 3:

• case 4:(要改插头)

• case 5:(要改插头)

• case 6:(要改插头)

• case 7:形成一个回路。只有最后一个格子才能形成一个回路。

练习题：

P3886 [JLOI2009]神秘的生物

这里面的题解也是我写的，和这篇一样难懂的风格。（包括代码风格）

[Code+#3]白金元首与莫斯科

这个大概有官方题解，你们自己找找吧。

还有 CDQ 的练习题表也挺好 ( 画红圈的那个和神秘的生物是一道题 ) ：

( 好不容易做一次 OI 网文写手，球点个赞吧 ! )