自动搬运

查看原文

来自洛谷，原作者为

	jun头吉吉 alive

搬运于2025-08-24 22:06:28，当前版本为作者最后更新于2020-07-15 15:55:22，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

题意

给出一张图，问执行多少次

• 选中一条边
• 把其他所有边减一

操作，可以使第$\texttt{Lab}$条边必然出现在这张图的最小生成树上

题解

看到题的第一秒：和[清华集训2012]最小生成树 好像啊

首先，根据相对运动的原理，我们知道，将其它边全部减小，就相当于将此边增大。因此，我们把整棵树的操作，改到了一条边上。

然后，我们考虑这么一张图：

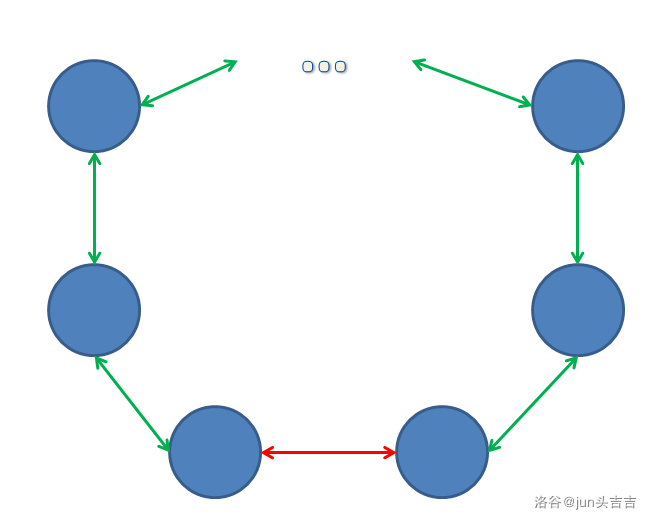
选取$\color{red}{\texttt{Lab}}$的条件是什么？显然，

• 如果环上有全部比$\texttt{Lab}$短，那么肯定是选那些更短的边
• 如果环上有和$\texttt{Lab}$一样长，那么二者肯定是二选一
• 如果环上有一条比$\texttt{Lab}$长的边，那么肯定是选$\texttt{Lab}$边

我们看一下题面：

使得标号为 $Lab$ 边一定出现最小生成树中的最少操作次数。

因此，不能有一条从$u_{Lab}$到$v_{Lab}$的路径，使边权全部$\leq d_{Lab}$，因此我们可以将所有$\leq d_{Lab}$的边组成一张图，割去$i$的代价为$d_{Lab}-d_i+1$，跑一遍最小割即为正解

#pragma optimize(2)
#include<bits/stdc++.h>
using namespace std;
template<typename T>
inline void read(T &x){
	x=0;char c=getchar();bool f=false;
	for(;!isdigit(c);c=getchar())f!=c=='-';
	for(;isdigit(c);c=getchar())x=x*10+c-'0';
	if(f)x=-x;
}
template<typename T ,typename ...Arg>
inline void read(T &x,Arg &...args){
	read(x);read(args...);
}
template<typename T>
inline void write(T x){
	if(x<0)putchar('-'),x=-x;
	if(x>=10)write(x/10);
	putchar(x%10+'0');
}
const int maxn=4010,maxe=100010*2;
struct Graph{
	struct node{
		int v,w,nxt;
	}e[maxe<<1];
	int head[maxn],cur[maxn],tot;
	int dis[maxn];
	int s,t;
	void init(int _s,int _t){s=_s,t=_t;tot=1;memset(head,0,sizeof head);}
	Graph(int _s=0,int _t=0){init(_s,_t);}
	void add(int u,int v,int w){
		//printf("%d %d %d\n",u,v,w);
		e[++tot]=(node){v,w,head[u]},head[u]=tot;
		e[++tot]=(node){u,w,head[v]},head[v]=tot;
	}
	#define v e[i].v
	inline bool bfs(){
		queue<int>q;
		memset(dis,0,sizeof dis);
		memcpy(cur,head,sizeof head);
		dis[s]=1;q.push(s);
		while(q.size()){
			int u=q.front();q.pop();
			for(int i=head[u];i;i=e[i].nxt)
				if(!dis[v]&&e[i].w){
					dis[v]=dis[u]+1,q.push(v);
					if(v==t)return true;
				}
		}
		return  false;
	}
	int dfs(int u,int flow){
		if(u==t)return flow;
		int rest=flow;
		for(int i=cur[u];i&&rest;i=e[i].nxt){
			if(dis[v]==dis[u]+1&&e[i].w){
				int tmp=dfs(v,min(rest,e[i].w));
				rest-=tmp,e[i].w-=tmp,e[i^1].w+=tmp;
			}
			cur[u]=i;
		}
		if(rest==0)dis[u]=-1;
		return flow-rest;
	}
	#undef v
	int dinic(){
		int ans=0;
		while(bfs())
			while(int sth=dfs(s,2e9))
				ans+=sth;
		return ans;
	}
}G;
int n,m,Lab;
int x[1000],y[1000],d[1000];
signed main(){
	read(n,m,Lab);
	for(int i=1;i<=m;i++)
		read(x[i],y[i],d[i]);
	G.init(x[Lab],y[Lab]);
	for(int i=1;i<=m;i++)
		if(i!=Lab&&d[i]<=d[Lab])
			G.add(x[i],y[i],d[Lab]-d[i]+1);
	write(G.dinic());
}