自动搬运

查看原文

来自洛谷，原作者为

	GalwayGirl 不想当司机的裁缝不是好oier

搬运于2025-08-24 22:06:26，当前版本为作者最后更新于2022-11-04 09:37:24，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

题意简述

初看题目，觉得很容易，就是让你将除了 $1$ 之外的两两互质的点建边，边权取决于出发点，问从 $s$ 到 $t$ 的最短路。

Solution

$n$ 的范围为 $4500$，互质的点建无向边的范围为将近 $3 \times 10 ^ 7$，暴力建边不成问题，那么跑边呢？恭喜你，喜提 50pts。

考虑本题与其他题目不同的地方，它的边权就是出发点。 再考虑一下 Dijkstra 的核心思想，就是贪心的将最短距离放入堆中，再提出来对终点进行松弛操作。对两种不同的边权画图分析。

1. 两点之间边权给出。

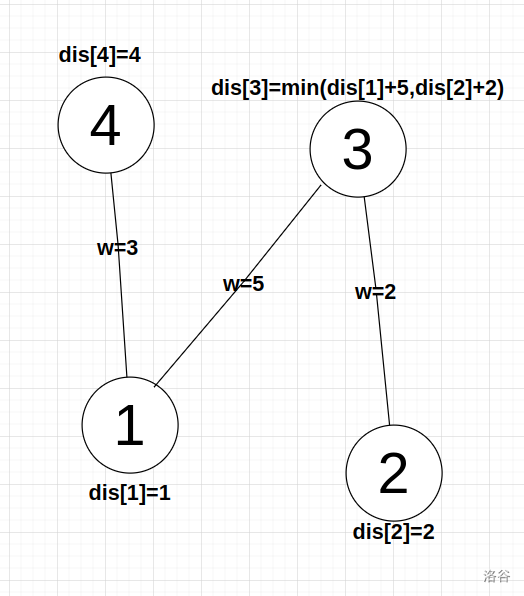
可以看到节点 1 和 节点 2 对 3 进行松弛，然后 1 又对 4 进行松弛，因为一个点与不同点的边权的差异性，导致每次都要将点提出来更新其他点。

2. 边权取决与点

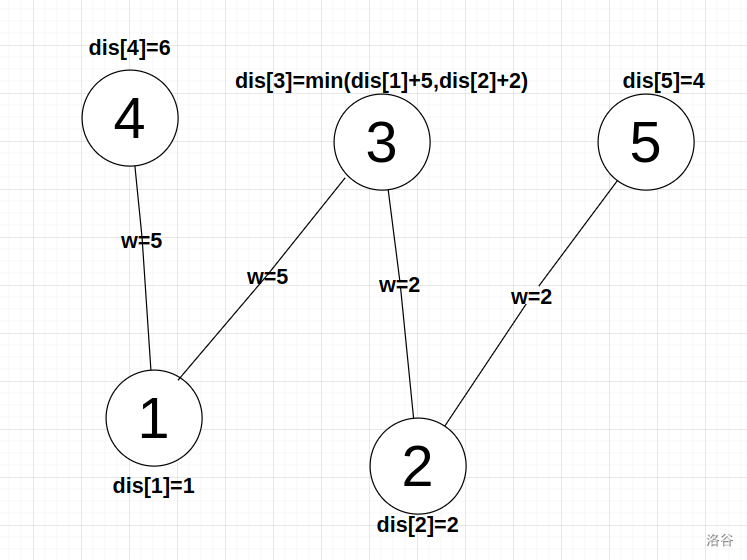
因为每个点到其他点的边权是相同的，所以上图与下图是等价的。

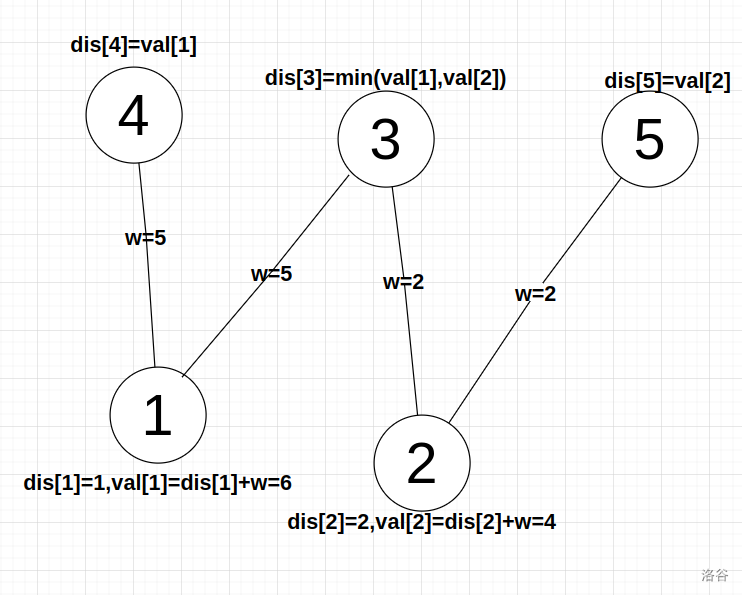
可以发现当点到其他点边权相同时，点权加上边权为定值，所以在放入堆中时可以将点权加边权作为排序关键字，进行松弛操作时提出来的点一定是最优的，直接赋值即可，具体操作见此处代码。

    S=read();T=read();
    for(int i=1;i<=n;i++)w[i]=read(),dis[i]=1e18,vis[i]=false;
    priority_queue<hh>q;
    q.push({S,w[S]});
    dis[S]=0;
    while(!q.empty()){
        int now=q.top().id;
        long long val=q.top().val;
        q.pop();
        if(vis[now])continue;
        vis[now]=true;
        for(int i=head[now];i;i=edge[i].next){
            int v=edge[i].to;
            dis[v]=val;
            if(v==T){
                printf("%lld\n",dis[T]);
                return;
            }
            q.push({v,dis[v]+w[v]});
        }
    }

所以在写类似优化的题时，一定要了解算法核心才能想办法优化。

最后贴上代码。

#include<bits/stdc++.h>
using namespace std;
const int M=3e7,N=4600;
int t,n,c,head[N],S,T,w[N];
long long dis[N];
bool vis[N];
inline int read(){
    int x=0,w=1;char ch=0;
    while(ch<'0'||ch>'9'){
        if(ch=='-')w=-1;
        ch=getchar();
    }
    while(ch>='0'&&ch<='9'){
        x=(x<<1)+(x<<3)+ch-'0';
        ch=getchar();
    }
    return x*w;
}
struct xzh{
    int next,to;
}edge[M*2];
struct hh{
    int id;
    long long val;
    bool operator <(const hh&x)const{
        return x.val<val;
    }
};
void add(int u,int v){
    c++;
    edge[c].next=head[u];
    edge[c].to=v;
    head[u]=c;
}
int gcd(int a,int b){
    if(b==0)return a;
    return gcd(b,a%b);
}
void pre(){
    for(int i=2;i<=n;i++){
        for(int j=i;j<=n;j++){
            if(gcd(i,j)==1)add(i,j),add(j,i);
        }
    }
}
void solve(){
    S=read();T=read();
    for(int i=1;i<=n;i++)w[i]=read(),dis[i]=1e18,vis[i]=false;
    priority_queue<hh>q;
    q.push({S,w[S]});
    dis[S]=0;
    while(!q.empty()){
        int now=q.top().id;
        long long val=q.top().val;
        q.pop();
        if(vis[now])continue;
        vis[now]=true;
        for(int i=head[now];i;i=edge[i].next){
            int v=edge[i].to;
            dis[v]=val;
            if(v==T){
                printf("%lld\n",dis[T]);
                return;
            }
            q.push({v,dis[v]+w[v]});
        }
    }
}
int main(){
    t=read();n=read();
    pre();
    while(t--)solve();
}