自动搬运

查看原文

来自洛谷，原作者为

	DDOSvoid **

搬运于2025-08-24 22:06:08，当前版本为作者最后更新于2018-11-05 18:58:15，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

好像没人 A 掉啊

果然毒瘤题，虽然不卡分块

另外写 solution 的人的语文烂的要死

updeta： 为什么这么多人直接交题解啊？

std 已经更改过，直接提交不能 AC 请自重（当然不影响阅读

Solution

测试点 1

逐秒模拟即可

测试点 2 ~ 6

暴力模拟，每个位置多记时间这个标记，复杂度 $O(nm)$

测试点 7 ~ 9

其实第 7 个点，暴力也能过

假设一个点的值为 v，考虑单点修改 a，看下面这个图（忽略了 $\times b$

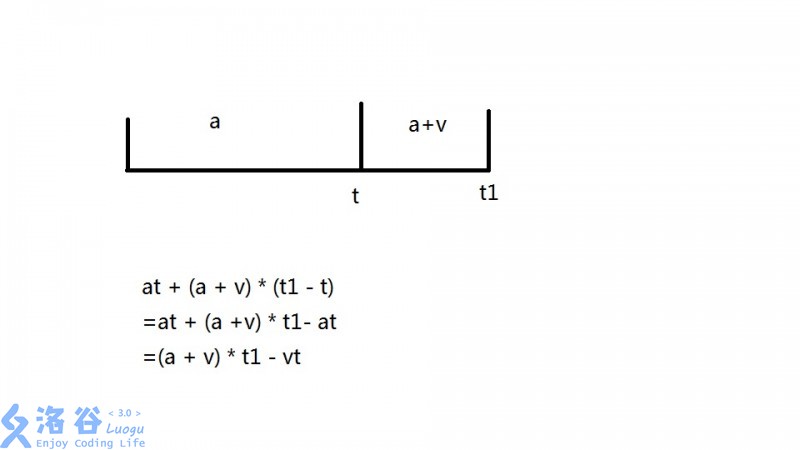
也就是说，如果在时间 $t$ 将 $a$ 增加 $v$，我们只需要 $sum-=v*b*t$ 即可，最终在时间 $t_1$ 查询时我们直接查询 $sum+a*b*t_1$，所以可用线段树维护区间和以及区间 $a*b$ 的和，修改就是单点修改，查询就是区间查询

测试点 10 ~ 11

观察 $a$ 的单点修改，修改的时候 $b$，$t$ 是常量，如果能维护 b 的区间和，那么是可以修改区间的，所以线段树 + 标记 即可

测试点 12 ~ 13

对 $b$ 仅有单点修改，所以上一种是一样的，再加一个对 b 的单点修改即可

测试点 14

仅有询问，所以直接线段树维护区间和以及区间 $a*b$ 的和即可

这个点好像没啥意义

测试点 15 ~ 17

仅仅是增加了 b 的区间修改，至此，我们的想法已经非常明确

即我们要维护 $\sum a$，$\sum v$，$\sum b$，$\sum a*b$，那么要维护这些值，我们需要一些标记

对于线段树处理多标记，有一个统一的规则，即对于线段树上的任意一个点，我们在递归到它的时候（即它的父亲的 tag 全部下放），它要维护的值一定是正确的。

所以接下来我们考虑的更新标记都是要传给子节点的标记

注意到 $\sum v$ 一定是形如 $\sum v - x*\sum a - y*\sum b+z$ 这种形式，下面我们根据操作还确定标记

考虑区间改 a 的操作，我们需要一个 $adda$ 标记，表示 $\sum v$ 还要减多少倍的 $\sum b$，还有一个标记 $Adda$，表示 a 增加了多少，在改 a 的时候 ($a+=v$），$adda+=v*t$，$Adda+=v$，如果之前对这个点有过区间改 b 的话，最后我们只是拿 $adda*\sum b$，而 $\sum b$ 是未更新的 $\sum b$，所以还要记一个标记 $addv$ 表示 $\sum v$ 要加上多少常量，$addv-=Addb*v*t$

区间改 b 的操作类似

区间改 v ...

现在考虑具体的标记下传到值

仅考虑左儿子的情况，形如 $adda'$ 为父亲的标记

$\sum v = \sum v-addb'*a-adda'*b+addv'*(m-l+1)$

$\sum ab=\sum ab+Adda'*Addb'*(m-l+1)+Adda'*\sum b+Addb'*\sum a$

$\sum a =\sum a + Adda'*(m-l+1)$

$\sum b=\sum b + Addb'*(m-l+1)$

注意更新顺序，下面考虑标记下传到标记

$addv=addv-addb'*Adda-adda'*Addb+addv'$

$adda=adda+adda'$

$addb=addb+addb'$

$Adda=Adda+Adda'$

$Addb=Addb+Addb'$

同样注意更新顺序

附上丑陋的 std

#include<iostream>
#include<cstdio>
#include<cctype>
#define maxn 500010
#define ll long long
#define gc getchar
using namespace std;

int n, m, a[maxn], b[maxn], v[maxn];

const int p = 1000000007;

int read(){
	int x = 0, f = 0; char c = gc();
	while(!isdigit(c)){if(c == '-') f = 1; c = gc();}
	while(isdigit(c)){x = x * 10 + c - '0'; c = gc();}
	return f ? -x : x;
}

#define lc i << 1
#define rc i << 1 | 1
struct seg{	
	ll v, a, b, adda, addb, addv, mul, Adda, Addb, Addmul;
}T[maxn * 4]; 
inline void maintain(int i){
	T[i].v = (T[lc].v + T[rc].v) % p;
	T[i].mul = (T[lc].mul + T[rc].mul) % p;
	T[i].a = (T[lc].a + T[rc].a) % p;
	T[i].b = (T[lc].b + T[rc].b) % p;
}	

void build(int i, int l, int r){
	if(l == r){
		T[i].v = v[l]; T[i].a = a[l]; 
		T[i].b = b[l]; T[i].mul = 1ll * a[l] * b[l] % p; return ;
	} int m = l + r >> 1;
	build(lc, l, m); build(rc, m + 1, r);
	maintain(i);
}

void pushdown(int i, int l, int r){
	ll &adda = T[i].adda, &addb = T[i].addb, &addv = T[i].addv; int m = l + r >> 1;
	ll &Adda = T[i].Adda, &Addb = T[i].Addb, &Addmul = T[i].Addmul;
	
	T[lc].v = (T[lc].v - adda * T[lc].b - addb * T[lc].a + addv * (m - l + 1)) % p;
	T[rc].v = (T[rc].v - adda * T[rc].b - addb * T[rc].a + addv * (r - m)) % p;
	T[lc].mul = (T[lc].mul + Adda * Addb % p * (m - l + 1) % p + Adda * T[lc].b + Addb * T[lc].a) % p;
	T[rc].mul = (T[rc].mul + Adda * Addb % p * (r - m) % p  + Adda * T[rc].b + Addb * T[rc].a) % p;
	T[lc].a = (T[lc].a + Adda * (m - l + 1)) % p; T[rc].a = (T[rc].a + Adda * (r - m)) % p;
	T[lc].b = (T[lc].b + Addb * (m - l + 1)) % p; T[rc].b = (T[rc].b + Addb * (r - m)) % p;
	
	T[lc].addv = (T[lc].addv + addv - T[lc].Adda * addb - T[lc].Addb * adda) % p;
	T[rc].addv = (T[rc].addv + addv - T[rc].Adda * addb - T[rc].Addb * adda) % p;
	
	T[lc].adda = (T[lc].adda + adda) % p;
	T[rc].adda = (T[rc].adda + adda) % p;
	
	T[lc].addb = (T[lc].addb + addb) % p;
	T[rc].addb = (T[rc].addb + addb) % p;
	
	T[lc].Adda = (T[lc].Adda + Adda) % p;
	T[rc].Adda = (T[rc].Adda + Adda) % p;
	
	T[lc].Addb = (T[lc].Addb + Addb) % p;
	T[rc].Addb = (T[rc].Addb + Addb) % p;
	
	//T[lc].Addmul = (T[lc].Addmul + Addmul) % p;
	//T[rc].Addmul = (T[rc].Addmul + Addmul) % p;
	
	adda = addb = addv = Adda = Addb = Addmul = 0;
}	

void update_adda(int i, int l, int r, int L, int R, ll v, ll t){
	if(l > R || r < L) return ;
	if(L <= l && r <= R){
		T[i].v = (T[i].v - T[i].b * v % p * t) % p;
		T[i].a = (T[i].a + 1ll * v * (r - l + 1)) % p; T[i].mul = (T[i].mul + T[i].b * v) % p;
		T[i].adda = (T[i].adda + 1ll * v * t) % p; 
		T[i].addv = (T[i].addv - T[i].Addb * v % p * t) % p;
		T[i].Adda = (T[i].Adda + v) % p; //T[i].Addmul = (T[i].Addmul + v * T[i].Addb) % p;
		return ;
	} int m = l + r >> 1; pushdown(i, l, r);
	update_adda(lc, l, m, L, R, v, t); update_adda(rc, m + 1, r, L, R, v, t);
	maintain(i);
}

void update_addb(int i, int l, int r, int L, int R, ll v, ll t){
	if(l > R || r < L) return ;
	if(L <= l && r <= R){
		T[i].v = (T[i].v - T[i].a * v % p * t) % p;
		T[i].b = (T[i].b + 1ll * v * (r - l + 1)) % p; T[i].mul = (T[i].mul + T[i].a * v) % p;
		T[i].addb = (T[i].addb + 1ll * v * t) % p;
		T[i].addv = (T[i].addv - T[i].Adda * v % p * t) % p;
		T[i].Addb = (T[i].Addb + v) % p; //T[i].Addmul = (T[i].Addmul + v * T[i].Adda) % p;
		return ;
	} int m = l + r >> 1; pushdown(i, l, r);
	update_addb(lc, l, m, L, R, v, t); update_addb(rc, m + 1, r, L, R, v, t);
	maintain(i);
}

void update_addv(int i, int l, int r, int L, int R, int v){
	if(l > R || r < L) return ;
	if(L <= l && r <= R){
		T[i].v = (T[i].v + 1ll * v * (r - l + 1)) % p;
		T[i].addv = (T[i].addv + v) % p;
		return ;
	} int m = l + r >> 1; pushdown(i, l, r);
	update_addv(lc, l, m, L, R, v); update_addv(rc, m + 1, r, L, R, v);
	maintain(i);
}

ll query(int i, int l, int r, int L, int R, int t){
	if(l > R || r < L) return 0;
	if(L <= l && r <= R) return (T[i].v + T[i].mul * t) % p;
	int m = l + r >> 1; pushdown(i, l, r);
	return (query(lc, l, m, L, R, t) + query(rc, m + 1, r, L, R, t)) % p;
}

inline void solve_1(){
	int t = read(), x = read(), y = read();
	ll v = query(1, 1, n, x, y, t); v = (v % p + p) % p;
	printf("%lld\n", v);
}

inline void solve_2(){
	int t = read(), x = read(), y = read(), z = read();
	update_adda(1, 1, n, x, y, z, t);	
}

inline void solve_3(){
	int t = read(), x = read(), y = read(), z = read();
	update_addb(1, 1, n, x, y, z, t);	
}

inline void solve_4(){
	int t = read(), x = read(), y = read(), z = read();
	update_addv(1, 1, n, x, y, z);	
}

int main(){
	n = read(); m = read();
	for(int i = 1; i <= n; ++i) v[i] = read(), a[i] = read(), b[i] = read();
	build(1, 1, n);
	for(int i = 1; i <= m; ++i){
		int opt; opt = read();
		switch(opt){
			case 1 : solve_1(); 
			case 2 : solve_2(); 
			case 3 : solve_3(); 
			case 4 : solve_4(); 
		}
	}
	return 0;
}