自动搬运

查看原文

来自洛谷，原作者为

	Imakf **

搬运于2025-08-24 22:06:06，当前版本为作者最后更新于2018-11-05 13:23:41，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

T4 中国象棋 - 摆上马

之前是这道题的，因为太水了就换了

本题受 [SCOI2005]互不侵犯，[AHOI2009]中国象棋，[NOI2001]炮兵阵地 启发而出

$20pts$ 爆搜

爆搜应该可以拿个$20$分

2AC & 8TLE

$50$~$80pts$ 状压dp

不妨设$dp[i][j][k]$为考虑到第$i$行，本行状态为$j$，上一行状态为$k$的方案数

初始化

先初始化第$1$行和第$2$行，然后dp

方便起见，我们把状态$i$可以攻击到状态$j$或者反过来，统称为$i$与$j$冲突

for(register int i=0; i< (1<<y); ++i )	dp[1][i][0]=1;//第一行怎么放都行，因为同一行不可能冲突

for(register int i=0; i< (1<<y) ; ++i) {
    for(register int j=0; j< (1<<y) ; ++j) {
        if(i与j冲突)	continue;
        dp[2][j][i]+=dp[1][i][0];
    }
}

转移

四层暴力枚举$i,j,k,s$分别表示

$i$ 当前考虑的行数

$j$ 当前考虑的行数的状态

$k$ 上一行的状态

$s$ 上上行的状态

for(register int i=3; i<=x; ++i) {
		for(register int j=0; j< (1<<y); ++j) {
			for(register int k=0; k< (1<<y); ++k) {
				if(j与k冲突)	continue;
				for(register int s=0; s< (1<<y) ; ++s) {
					if(s与k冲突||s与j冲突)	continue;
					dp[i][j][k]+=dp[i-1][k][s];
					dp[i][j][k]%=mod;
				}
			}
		}
	}

判断冲突

我们需要$2$个函数来判断出某一行可以攻击到的范围

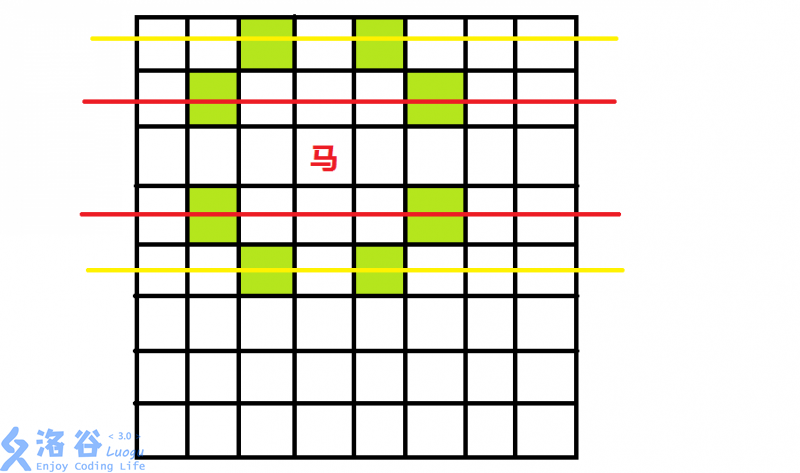
我们用函数$at$_$bt(a)$计算出红线经过的攻击范围，图中为$(01000100)_2$

用另一个函数$at$_$3(a,b)$表示第$i$行为状态$a$,第$i+1$行状态为$b$,第$i$行可以攻击到$i+2$行的范围（图中黄色线经过的区域），图中为$(00101000)_2$

先设计$at$_$bt(a)$,以下图为例（红色代表放了马）

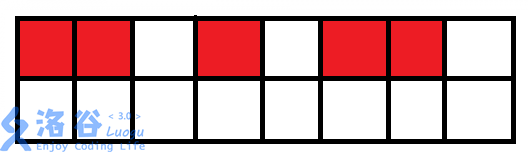
从右往左考虑

第一个格子没有马，下一个

第二个格子有马，右边有没有马？

没有，那么可以攻击第二行往右数第二个格子，左边有没有马？

有，那么攻击不到第二行往左数第二个格子

于是第二行变成

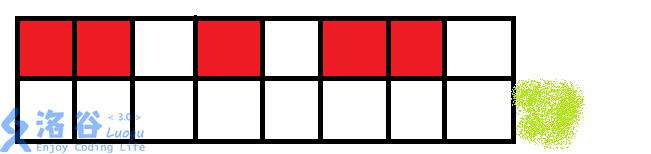
第三个格子有马，右边有没有马？

有，那么攻击不到第二行往右数第二个格子，左边有没有马？

没有，那么可以攻击第二行往左数第二个格子

于是第二行变成

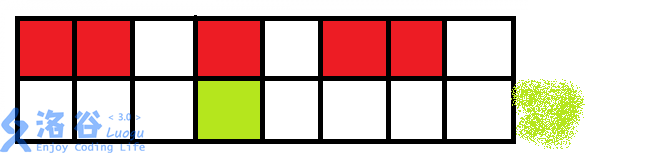
按照这样，最终第二行变成了

攻击范围就是$(01010100)_2$

于是我们很自然的写出这样的代码

inline int bit(int a,int x){
	//返回a的二进制第x位并保留右侧的0
	//也就是说bit(5,3)==4
    if(x<1)	return 0;
    return a&(1<<(x-1));
}
inline int check(int a,int x){ //返回a的二进制第x位是否为1
	if(x<1)	return 0;
    if(a&(1<<(x-1)))	return 1;
    return 0;
}

int at_bt(int a){ //求出状态a对于下一行的攻击范围
    int c=0;
    for(register int i=1; bit(-1,i)<=a; ++i){
        if(!check(a,i))	continue; //判断有马
        if(check(a,i)&check(a,i-1));
        else c|=bit(-1,i-2); //同下
        if(check(a,i)&check(a,i+1));
        else c|=bit(-1,i+2); //注意是|
    }
    return c;
}

然后考虑设计$at$_$3(a,b)$，这个比较简单，以下图为例（暂且不考虑这两行的矛盾）

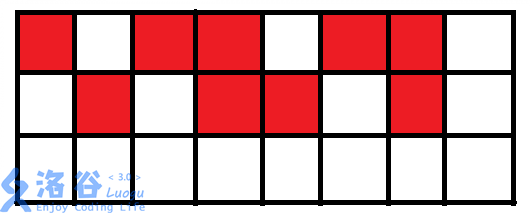
依然第一行从右往左考虑

第一个格子有没有马？

没有，下一个

第二个格子有没有马？

有，下一行的第二个格子有没有马？

有，所以被别住了，下一个

第三个格子有没有马？

有，下一行的第二个格子有没有马？

没有，所以不会被别住，就可以攻击下方的两个格子，于是变为

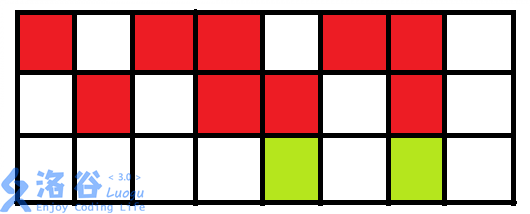
于是乎这样子，最后变为

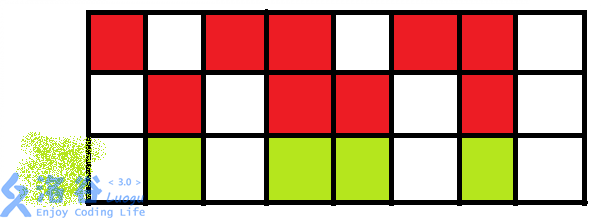
于是我们也可以自然的写出下列代码

int at_3(int a,int b){
	//a表示第一行状态
    //b表示第二行状态
    int c=0;
    for(register int i=1; bit(-1,i)<=a; ++i){
        if(!check(a,i))	continue;
        if(check(a,i)&check(b,i));
        else c|=bit(-1,i-1),c|=bit(-1,i+1);//注意是|
    }
    return c;
}

于是问题解决了，之前的转移代码可以改成

    for(register int i=3; i<=x; ++i) {
	for(register int j=0; j< (1<<y); ++j) {
		for(register int k=0; k< (1<<y); ++k) {
			if(at_bt(k)&j||at_bt(j)&k)	continue;
			for(register int s=0; s< (1<<y) ; ++s) {
				if(at_bt(s)&k|| at_bt(k)&s ||at_3(s,k)&j || at_3(j,k)&s)	continue;
				dp[i][j][k]+=dp[i-1][k][s];
				dp[i][j][k]%=mod;
			}
		}
	}
}

最后统计答案

long long ans=0;
for(register int i=0; i<(1<<y); ++i) {
	for(register int j=0; j<(1<<y); ++j) {
		if(at_bt(i)&j||at_bt(j)&i)	continue;
		ans+=dp[x][i][j];
		ans%=mod;
	}
}

$100pts$ 滚动数组优化

您注意到$1MB$的空间限制了，然后就来优化空间吧，把所有枚举行数的都加上$\mod 3$就好了，最后统计答案也要加上！

$100pts$ 时间优化

为了时间好看一点，您可以储存攻击范围，时间会大大加快，空间也不会炸！

$100pts$ 打表

嗯……前提是您要打得出来