1 条题解

  • 0
    @ 2025-8-24 22:05:55

    自动搬运

    查看原文

    来自洛谷，原作者为

    avatar 周道_Althen
    **

    搬运于2025-08-24 22:05:55，当前版本为作者最后更新于2018-10-14 17:23:12，作者可能在搬运后再次修改，您可在原文处查看最新版

    自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

    以下是正文

    大家好我是出题人 Althen·Way·Satan（超小声）。

    热烈祝贺第一个切掉这个题的人：@南山桥一霸；

    还有感谢一直到最后都在肝我的题的大佬，葱花都要哭出来了：@zhaimingshuzms。（Orz，都已经拿到70%了）

    • 前排鸣谢：

           \ \ \ \ \ \ \ 指导（PY关系）：@Psyduck

           \ \ \ \ \ \ \ SPJ友情提供：@hdxrie

           \ \ \ \ \ \ \ 表情包出处：@全兽出击   \ \ 画师：@呀嘛的小2狼 （大家快去关注他呀XD）

    一、题面解释

           \ \ \ \ \ \ \ 根据题面所描述的意思，我们可以得到如下的图形：

           \ \ \ \ \ \ \ 吃瓜

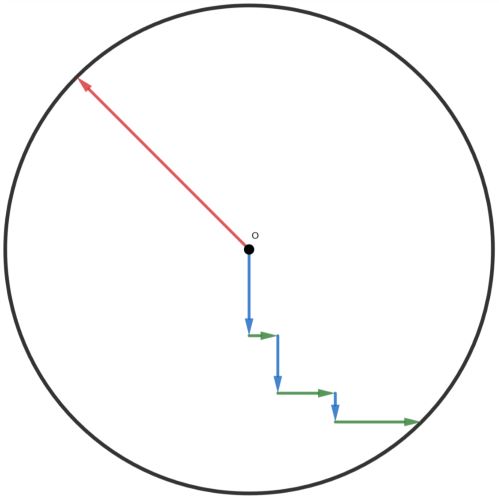
           \ \ \ \ \ \ \ 其中，绿色和蓝色的箭头代表 Althen \ \rm Althen\ 走过的路程；红色的箭头代表 hdxrie \ \rm hdxrie\ 走过的路程，设时间为 T \ T\ 的话，红色箭头的长度便为 C(x)×T \ C(x)×T\ 。

           \ \ \ \ \ \ \ 斜眼

           \ \ \ \ \ \ \ Althen \rm Althen\ 走路扭来扭去的，不方便研究，让人十分不爽。我们不妨 （把他拖出去打一顿）平移一下他走过的路程：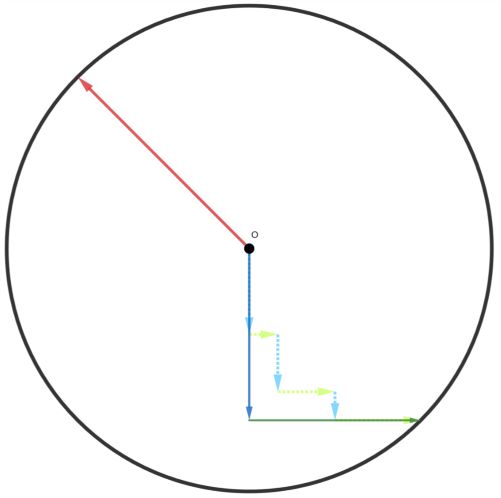

           \ \ \ \ \ \ \ 发光

           \ \ \ \ \ \ \ 平（dǎlē）移（yídùn）过后，看起来舒服多了呢，那么现在，我们可以度量一下 Althen \ \rm Althen\ 走过的路程，根据题面定义， 可以发现绿色箭头的长度为 A(x)×T \ A(x)×T\ ，绿色箭头的长度为 B(x)×T \ B(x)×T\ 。容易证明，不管 Althen \ \rm Althen\ 怎么扭，都可以通过平移得到这样的表达式（小学数学）。

           \ \ \ \ \ \ \ 托腮

           \ \ \ \ \ \ \ 通过观察我们可以很容易发现，红色箭头的长度 C(x)×T \ C(x)×T\ 就刚刚好等于半径，所以我们不妨把他也旋转下来：

           \ \ \ \ \ \ \ 吃鲸！？

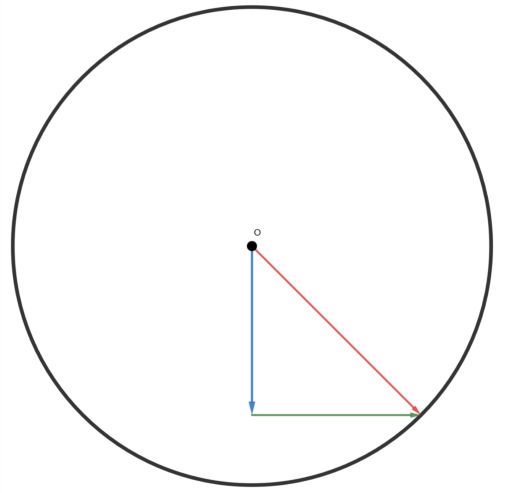
           \ \ \ \ \ \ \ 这是一个直角三角形，我们可以轻易写出下面的式子（初中数学）：

    (C(x)×T)2=(A(x)×T)2+(B(x)×T)2(C(x)×T)^2=(A(x)×T)^2+(B(x)×T)^2

           \ \ \ \ \ \ \ 化简过后可以得到：

    C2(x)=A2(x)+B2(x)C^2(x)=A^2(x)+B^2(x)

           \ \ \ \ \ \ \ 所以说，我们定义函数f(x)f(x):

    f(x)=C2(x)−A2(x)−B2(x)f(x)=C^2(x)-A^2(x)-B^2(x)

           \ \ \ \ \ \ \ 拇指

           \ \ \ \ \ \ \ 求出函数f(x)f(x)在[L,R][L,R]范围的根，就是我们要求的系数xx了。

           \ \ \ \ \ \ \ 注意，速度是矢量，所以就算我们解出来的根 x\ x，带进原函数 A(x)\ A(x)，B(x)B(x)，C(x) C(x)\ 是负数，它也是合法的，这是高一的物理，题面最后也给了提示：$\color{#EEE}{\tt {Notice\ that\ SPEED\ is\ VECTOR.(High\ school\ physics)}}$。

    二、分段解析

    • type1(10%): \ L==RL==R

           \ \ \ \ \ \ \ 答案只有可能为 L\ L，直接判断该答案是否满足f(L)==0f(L)==0，既是否满足C2(x)−A2(x)−B2(x)==0C^2(x)-A^2(x)-B^2(x)==0。

           \ \ \ \ \ \ \ 斜眼

           \ \ \ \ \ \ \ 应该是读懂题意即可拿的分。

    • type2(20%): \ La=Lb=Lc=1La=Lb=Lc=1

           \ \ \ \ \ \ \ 因为保证La=Lb=Lc=1La=Lb=Lc=1，函数形式就保证为：A(x)=a1x+a0A(x)=a_1x+a_0，B(x)=b1x+b0B(x)=b_1x+b_0，C(x)=c1x+c0C(x)=c_1x+c_0。

           \ \ \ \ \ \ \ f(x)f(x)的形式也可以保证为：

    $$f(x)=(c_1^2-a_1^2-b_1^2)x^2+2(c_1c_0-a_1a_0-b_1b_0)x+c_0^2-a_0^2-b_0^2 $$

           \ \ \ \ \ \ \ 托腮

           \ \ \ \ \ \ \ 嗯……是一个二次函数呢，求根公式一波带走（初中数学）。

    • type3(30%): \ 保证[L,R][L,R]最多只有一个参数xx合法；

           \ \ \ \ \ \ \ 这相当于保证了f(x)f(x)在[L,R][L,R]内最多只有一个零点，f(x)f(x)在[L,R][L,R]内近似于单调。

           \ \ \ \ \ \ \ 发光

           \ \ \ \ \ \ \ 很容易想到二分答案，也确实可以二分答案（高一数学）。

           \ \ \ \ \ \ \ 注意，如果二分的**check( )写的是C2(x)−A2(x)−B2(x)C^2(x)-A^2(x)-B^2(x)的值，可能会造成比较大的精度误差，建议老老实实先算出f(x)f(x)，再check( )**判断f(x)f(x)的值。

           \ \ \ \ \ \ \ 在求f(x)f(x)的过程中，需要求到卷积，我们发现O(n2)O(n^2)地求卷积代价太大，所以推荐使用 快速傅里叶变换FFTFFT ，不会就出门左拐百度，会有很多大佬的讲解的。

    • type_all(100%)

           \ \ \ \ \ \ \ 哭唧唧

           \ \ \ \ \ \ \ 没有什么特殊性质，因为可能有多个根，也不能二分了呢。

           \ \ \ \ \ \ \ 托腮

           \ \ \ \ \ \ \ 回到我们的问题，是如何求f(x)f(x)在[L,R][L,R]内的任意一个解。

           \ \ \ \ \ \ \ 其实不过是个 牛顿迭代 的裸题，牛顿迭代常用于求一连续可导函数某一极值，或者某一零点。

           \ \ \ \ \ \ \ 吃瓜

           \ \ \ \ \ \ \ 这不就正是我们所需要的吗？

           \ \ \ \ \ \ \ 根据一阶牛顿迭代的公式，我们可以得到我们的答案就应该是以下函数的收敛值：

    $$F(x)=F(x-1)-\frac{f\left(F(x-1)\right)}{f'\left(F(x-1)\right)} $$

           \ \ \ \ \ \ \ 这里又需要求f(x)f(x)的一阶导f′(x)f'(x)，其实很简单，幂函数的导数网上一搜就有了。显然，我们后面的几个点，是满足f(x)f(x)二阶可导的，所以F(x)F(x)必然会收敛，但是不一定是在[L,R][L,R]内，需要判断一下。

    • 下面给出标程代码

    已经做了防抄袭处理，直接复制会CE的，XD\color{#EEE}{\text{已经做了防抄袭处理，直接复制会CE的，XD}}

    #include<algorithm>
#include<iostream>
#include<cstdlib>
#include<cstring>
#include<cctype>
#include<cstdio>
#include<string>
#include<queue>
#include<stack>
#include<cmath>
#include<map>
#include<set>
using　namespace　std;
const　double　eps=1e-10;
const　double　pi=acos(-1.0);
inline　int　read(){
　　int　x=0,f=1;char　ch;ch=getchar();
　　while(ch<'0'||ch>'9'){if(ch=='-')　f=0;ch=getchar();}
　　while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch&15);ch=getchar();}
　　if(f)return　x;else　return　-x;
}
double　fabs(double　c){if(c<0.0)return　-c;return　c;}
const　int　N=3e5+10;
//FFT模板————————————————————————————————————　
struct　cpx{
　　double　r,i;
　　inline　cpx　operator　*(const　cpx&x)const{return　(cpx){r*x.r-i*x.i,r*x.i+i*x.r};}
　　inline　cpx　operator　+(const　cpx&x)const{return　(cpx){r+x.r,i+x.i};}
　　inline　cpx　operator　-(const　cpx&x)const{return　(cpx){r-x.r,i-x.i};}
}cpxa[N],cpxb[N];
int　r[N];
void　FFT(cpx*a,int　f,int　la){
　　int　n=la;
　　for(register　int　i=0;i<n;++i)if(i<r[i])swap(a[i],a[r[i]]);
　　for(register　int　i=1;i<n;i<<=1){
　　　　cpx　wn=(cpx){cos(pi/i),f*sin(pi/i)};
　　　　for(register　int　j=0;j<n;j+=(i<<1)){
　　　　　　cpx　w=(cpx){1,0};
　　　　　　for(register　int　k=0;k<i;++k,w=w*wn){
　　　　　　　　cpx　x=a[j+k],y=w*a[j+k+i];
　　　　　　　　a[j+k]=x+y;a[j+k+i]=x-y;
　　　　　　}
　　　　}
　　}
　　if(f==-1)
　　for(register　int　i=0;i<n;i++)a[i].r/=n;
}
int　merge_fft(cpx　*a,cpx　*b,int　la,int　lb){
　　int　n=la,m=lb;
　　int　L=0;for(m+=n,n=1;n<=m;n<<=1)L++;
　　for(register　int　i=0;i<n;i++)
　　r[i]=(r[i>>1]>>1)|((i&1)<<(L-1));
　　FFT(a,1,n);FFT(b,1,n);
　　for(register　int　i=0;i<=n;i++)a[i]=a[i]*b[i];
　　FFT(a,-1,n);
　　return　m;
}
//————————————————————————————————————————　
double　L,R;
int　La,Lb,Lc,Lc1,a[N],b[N],c[N],c1[N];
//函数平方
void　get_square(int　*a,int　&L){　
　　memset(cpxa,0,sizeof(cpxa));
　　memset(cpxb,0,sizeof(cpxb));
　　for(register　int　i=0;i<=L;i++)
　　cpxb[i].r=cpxa[i].r=(double)a[i];
　　L=merge_fft(cpxa,cpxb,L,L);
　　for(register　int　i=0;i<=L;i++)a[i]=(int)(cpxa[i].r+0.1);
}
//求C(x)的值
double　get_val_C(double　x){
　　double　X=1,Ret=0;
　　for(int　i=0;i<=Lc;i++){Ret=Ret+c[i]*X;X=X*x;}
　　return　Ret;
}
//求C1(x)的值
double　get_val_C1(double　x){
　　double　X=1,Ret=0;
　　for(int　i=0;i<=Lc1;i++){Ret=Ret+c1[i]*X;X=X*x;}
　　return　Ret;
}
//牛顿迭代　———————————————————————————————————　
int　tim=30;//设定迭代次数tim　
double　Newton_Iteration(double　x){//输入F(x)的初值F(0)，既迭代系数。　
　　double　c;
　　while(1){
　　　　c=get_val_C(x);//求出f(F(x))的值　
		　　tim--;
　　　　if(fabs(c)<eps)break;//若是F(x)在该精度下已经合法，便弹出。　
　　　　x=x-c/get_val_C1(x);//求出F(x)-f(F(x))/f'(F(x))的值，赋给F(x+1)　
　　　　x=max(x,L);x=min(x,R);//防止越界　
　　　　if(!tim)return　0;//若是在迭代次数tim内不合法，便弹出无解。　
　　}
　　return　x;
}
int　main()
{
　　La=read();Lb=read();Lc=read();scanf("%lf%lf",&L,&R);
　　for(int　i=0;i<=La;i++)a[i]=read();
　　for(int　i=0;i<=Lb;i++)b[i]=read();
　　for(int　i=0;i<=Lc;i++)c[i]=read();
　　for(register　int　i=0;i<=La;i++)
　　cpxb[i].r=cpxa[i].r=(double)a[i];
　　
　　//把c^2(x)-a^2(x)-b^2(x)存进c　
　　get_square(a,La);
　　get_square(b,Lb);
　　get_square(c,Lc);
　　Lc=max(Lc,max(La,Lb));
　　for(register　int　i=0;i<=Lc;i++)
　　c[i]=c[i]-b[i]-a[i];
　　
　　//求c1(x)为c(x)的一阶导数　
　　Lc1=Lc-1;
　　for(int　i=1;i<=Lc;i++)
　　c1[i-1]=c[i]*i;
　　
　　double　ans=Newton_Iteration((L+R)/2.0);
　　if(tim)　printf("%.8lf\n",ans);
　　else　printf("Inconsistent!\n");
　　return　0;
}

          \ \ \ \ \ \ 这道题就这样解完了。

           \ \ \ \ \ \ \ 题面清晰，解法自然，码量适中

           \ \ \ \ \ \ \ 吃鲸什么？

           \ \ \ \ \ \ \ 你不会牛顿迭代？那么我们马上进入下一个阶段。

    三、重点考点总结——牛顿迭代

           \ \ \ \ \ \ \ 这里简单地讲一下** 一阶牛顿迭代 **，牛顿迭代是应用在最优化领域非常重要的一种算法，由于具有二阶收敛性，所以相比二分法能大大降低迭代次数，只能求一个可导函数的零点，或者有二阶导函数的极值，一种全局搜索算法用来解np问题最优解的算法，在算法竞赛中的运用比较少见（Psyduck说）。

           \ \ \ \ \ \ \ 先放wiki的动图，牛顿迭代动态示例图：

           \ \ \ \ \ \ \ 容易看出一个重要问题：对函数的一个点做切线，这个切线与xx轴的交点当做新的点，重复操作，得到的点就会越来越趋近于零点。

           \ \ \ \ \ \ \ 具体证明涉及 泰勒展开，就不细讲了（其实是葱花Althen不会证明）。

           \ \ \ \ \ \ \ 说到函数切线，自然就需要求导。

           \ \ \ \ \ \ \ 在 f(x) \ f(x)\ 上，点 x=a \ x=a\ 的斜率为f′(a)f'(a)，所以这个切线与xx轴的交点当做新的点，应该是 a−f(a)f′(a) \ a-\frac{f\left(a\right)}{f'\left(a\right)}\ 。

           \ \ \ \ \ \ \ 所以，我们定义:

    $$F(x)=F(x-1)-\frac{f\left(F(x-1)\right)}{f'\left(F(x-1)\right)} $$

           \ \ \ \ \ \ \ 也就是不断去求点，可得这个点是越来越趋近某一个零点的。也就是说，我们的答案，就是 F(+∞) \ F(+∞)\ ，既函数 F(x) \ F(x)\ 的收敛值。

           \ \ \ \ \ \ \ 若f(x)f(x)二阶可导，那么在待求的零点 F(+∞) \ F(+∞)\ 值周围存在一个区域，只要起始点 F(0) \ F(0)\ 位于这个邻近区域内，那么牛顿迭代必定收敛。

           \ \ \ \ \ \ \ 托腮

           \ \ \ \ \ \ \ 不过……我们显然不需要算无限次，保证精度在一个范围内就行了，显然，牛顿迭代可以做到极快收敛到我们需要的精度，我们并不需要计算太多次。

           \ \ \ \ \ \ \ 吃鲸还有！

           \ \ \ \ \ \ \ 我们最终答案的计算效率、精度，还与迭代系数，也就是最初赋值的 F(0) \ F(0)\ 有很大关系。（但是因为比较小的x取值范围，本题没有卡迭代系数的选定）。

           \ \ \ \ \ \ \ 吃瓜

           \ \ \ \ \ \ \ 然后贴出一阶牛顿迭代的模板：

           \ \ \ \ \ \ \ （如果迭代次数过少或者无解，那么会返回一个错误的答案）

    double Newton_Iteration(double F,int tim){//输入迭代系数F=F(0)，迭代次数tim
  while(tim--)F=F-f(F)/f1(F);//f1(x)=f'(x)
  return F;
}

           \ \ \ \ \ \ \ 这里只是简单地讲一下** 一阶牛顿迭代 **，具体的讲解，有兴趣可以戳下面的链接，博主觉得讲得很清晰 （还有互交动画啊XD） 。

           \ \ \ \ \ \ \ --·--·--《推荐讲解文章》--·--·--

    如果对本题还有什么疑问或者更好的做法，欢迎洛谷私信我或者发送邮件到althenwaysatan@foxmail.com

    $\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ $发光

    • 1

    逃离

    信息

    ID
    3975
    时间
    1000ms
    内存
    63MiB
    难度
    6
    标签
    递交数
    0
    已通过
    0
    上传者
    1. 关于
    2. 联系我们
    3. 隐私
    4. 服务条款
    5. Language
    6. 主题
    3. Worker 0, 44ms