自动搬运

查看原文

来自洛谷，原作者为

	DPair その真っ白な心に、これからたくさんの思い出を。未来を想い、少女は少年に名を赠る。

搬运于2025-08-24 22:05:52，当前版本为作者最后更新于2019-05-07 20:17:37，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

楼下的巨佬都没有详细讲证明啊，在此我简单说一下详细证明

【思路】

这道题经过建模易得出，我们要求的就是有$n$个节点的有根树可能的形态数。

最后得出一个公式（有证明）

代码就出来了，不过重要的是证明部分

#include <bits/stdc++.h>
using namespace std;
#define LL long long
#define MOD 1000000009
LL ksm(LL n, LL m)
{//快速幂
    LL ret = 1;
    while(m) 
    {
        if(m & 1) ret = (ret * n) % MOD;
        n = (n * n) % MOD;
        m >>= 1;
    }
    return ret;
}
int main()
{
    int k;
    scanf("%d", &k);
    while(k --) 
    {
        LL n;
        scanf("%lld", &n);
        printf("%lld\n", ksm(n, n-1));
    }
}

【证明】（重点）

p.s 学习自https://www.cnblogs.com/dirge/p/5503289.html

首先引入$prufer$编码（这个单词的正确写法不是这样，但是很难打出来，以下以此代称）

一棵无根树的$prufer$编码的值运算如下：

首先定义无根树中度数为1的节点是叶子节点。
找到编号最小的叶子并删除，序列中添加与之相连的节点编号，重复执行直到只剩下2个节点。

（转载自https://www.cnblogs.com/dirge/p/5503289.html）

举个例子，对于下图的树

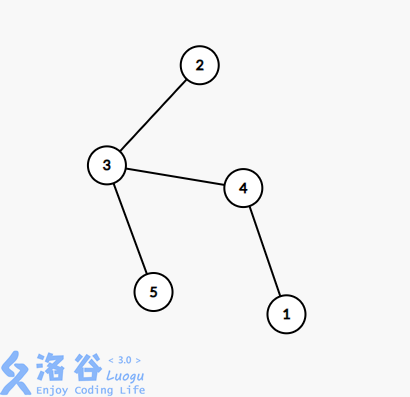
它的$prufer$编码就是4, 3, 3

显然，一棵有$n$个结点的无根树，它的$prufer$编码是唯一的，且有$n-2$个可能相同的元素。

那么如何由一个$prufer$编码转化为二叉树？

那个博客上的巨佬是这么说的：

设点集V={1,2,3,...,n}，每次取出prufer序列中最前面的元素u，在V中找到编号最小的没有在prufer序列中出现的元素v，给u，v连边然后分别删除，最后在V中剩下两个节点，给它们连边。最终得到的就是无根树。

很显然，每一个$prufer$序列与一棵无根树一一对应。

因此，对于一棵已知有$n$个结点的无根树，一定有一个$n-2$长度的序列，那么，我们枚举所有长度为$n-2$的序列，发现其与所有可能形态的无根树一一对应。而这种序列，根据乘法原理，有

个可能的序列。

因此，对于一个已知的$n$，有$n^{n-2}$种不同的无根树。

而由于无根树没有根，而题目要求的是有根树，因此，对于一棵$n$个结点的无根树，我们有$n$种选根的可能。

因此，对于一个已知的$n$，有$n^{n-2} * n$即$n ^ {n-1}$种不同的有根树。

证毕。