自动搬运

查看原文

来自洛谷，原作者为

	Sooke 做被自己雪藏的耳廓狐 | https://codeforces.com/profile/Sulfox

搬运于2025-08-24 22:05:49，当前版本为作者最后更新于2018-11-23 13:27:20，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

解题思路

把所谓的“菱树”转一下，我们就从一个类似树的玩意儿得到了一个类似网格图的玩意儿。

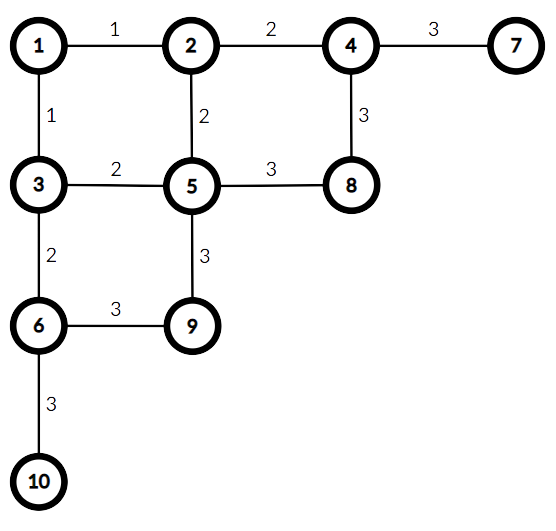
同时，有很多有趣的性质可以利用。

性质一：任意两点的最短路走的边数也最少。

或者说，最短路走边的方向不超过两种。如果有三种及以上，一定是在网格图上绕了远路，这与最短路的定义矛盾。

也许你会问：这网格图有边权的啊？绕路说不定更优吗？

的确，但这题很特殊，离 $1$ 号点越远的边边权越大，这意味着绕路的边权总和大于直接走的边权总和。

性质二：最短路一定先向 $1$ 号点靠近，再远离 $1$ 号点。

首先，性质一告诉我们最短路走边的方向不超过两种，而任意选择两个点，具体的一两种方向我们是可以计算出的。

那既然方向已知，又因为离 $1$ 号点越远的边边权越大，先靠近 $1$ 号点，再远离 $1$ 号点也就不难想了。

性质三：设 $u$ 在 $(x_u,\ y_u)$（网格图的第 $x_u$ 行第 $y_u$ 列），$v$ 在 $(x_v,\ y_v)$，靠近、远离 $1$ 号点的转折点在 $(min\{x_u,\ x_v\},\ min\{y_u,\ y_v\})$。

结合前面的性质多画画图感性理解就好了。

性质四：点 $u\ (u > 1)$ 到 $1$ 号点的距离 $= C_{x_u + y_u - 1}^{2}$

点 $u$ 在树中深度 $= x_u + y_u - 1$，连向父亲的边权自然 $= x_u + y_u - 2$，然后小学奥数算等差数列和。

性质五：点 $u,\ v$ 的最短路 $= C_{x_u + y_u - 1}^{2} + C_{x_v + y_v - 1}^{2} - 2C_{min\{x_u,\ x_v\} + min\{y_u,\ y_v\} - 1}^{2}$

把到 $1$ 号点的路径理解为"前缀和"，结合性质三、四思考。

有了这些性质，大致的思路应该也有了吧？

最后，怎么知道 $u$ 在网格图上的位置呢？

满足 $x_u + y_u - 1 = 1$ 的结点只有 $1$ 个，满足 $x_u + y_u - 1 = 2$ 的结点有 $2$ 个，满足 $x_u + y_u - 1 = 3$ 的结点有 $3$ 个……貌似很有规律。可以二分 $x_u + y_u - 1$ 的值，当然也可以解二次方程 $O(1)$ 算出。

然后？这道题就做完了。