自动搬运

查看原文

来自洛谷，原作者为

	Binary_Search_Tree 博客 https://cnblogs.com/bestlxm

搬运于2025-08-24 22:05:44，当前版本为作者最后更新于2019-07-21 12:53:21，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

题目传送门

考虑到可能出现的字符串不止一个，我们建立一棵字典树，将字典树上的节点看作一个串。

如果这个串可能出现，则把它涂黑。

因为每次操作都可以不按，所以第i-1次操作后的黑色节点在第i次操作后仍然是黑色。

如果按下，则会有新的黑色节点产生。

所以这是一个不断扩展的过程。

为了方便，我们暂时不考虑u。

假设我们现在进行第i次操作，字母为s[i]。

每个黑色节点的第s[i]个儿子都可以被涂黑。

那么现在的黑色节点的数量是原先的两倍吗？

显然不是。

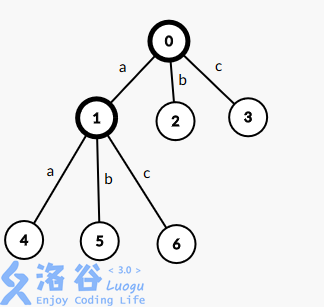
（为了方便，假设只有三种不同的字母）

如上图所示，0和1已经变为黑节点。若再按下a,则0->1,1->2

发现1号节点重复出现。

因此，我们需要一个数组，F[i]表示当前状态下有多少黑色节点已经有第i个儿子，转移时应减去它们产生的节点。

因此，第i次黑色节点=第(i-1)次黑色节点 * 2 - F[s[i]]。

现在问题就转化为了如何不断更新F[i]。

假如现在执行第i次操作

所有黑色节点跳到第s[i]个儿子的位置。

那么，所有原来的黑色节点都拥有第s[i]个儿子，因此，F[s[i]]更新为第i-1次操作后的黑色节点数量。

而对于其他的字符j，所有黑色节点中有第j个儿子的节点数量并没有发生变化，不需要更新。

就这样愉快地解决了吗？

我们还要考虑退格的情况。

如果一个字符串先在末尾加了一个字符，然后又删掉了，相当于一直没有变化。

所以，我们只需要考虑真实操作串都是u的串。这其实是在字典树中不断往上跳的过程。

所以，我们每遇到一个u,直接把答案+1就可以了。

但是，如果当前串已经删成空串了，就可以直接跳过这个过程。

那么F数组如何更新呢？

我们考虑统计到目前为止u的总个数cnt,那么现在删掉的是第1个串中的第(n-cnt+1)个字符。

对于这个字符s,我们只需要将F[s]++即可。

时间复杂度O(n)。

#include <cstdio>
#include <cstring>
#include <cmath>
#include <iostream>
#include <algorithm>
#define mod 19260817 //一个神秘的模数
#define M 10000005
using namespace std;
int n,m,cnt;//cnt表示当前删的位置
char A[M],B[M];
long long ans=1,F[30];
int main(){
	scanf("%d%d%s%s",&n,&m,A+1,B+1);cnt=n;//读入
	for (int i=1;i<=m;i++)
		if (B[i]>='A'&&B[i]<='Z'){
			long long tmp=F[B[i]-'A'+1];
			F[B[i]-'A'+1]=ans;//更新F数组
			ans=((ans+ans-tmp)%mod+mod)%mod;//更新ans
		}
		else {
			if (!cnt) continue;//如果当前串删完了就跳过
			F[A[cnt]-'A'+1]=(F[A[cnt]-'A'+1]+1)%mod;//更新F数组
			ans=(ans+1)%mod;cnt--;//更新ans
		}
	printf("%lld",ans);
	return 0;
}