自动搬运

查看原文

来自洛谷，原作者为

	丨Sky灬丨无惧 朕与将军解战袍，芙蓉帐暖度春宵。但使龙城飞将在，从此君王不早朝。

搬运于2025-08-24 22:05:31，当前版本为作者最后更新于2020-03-26 10:44:21，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

题解

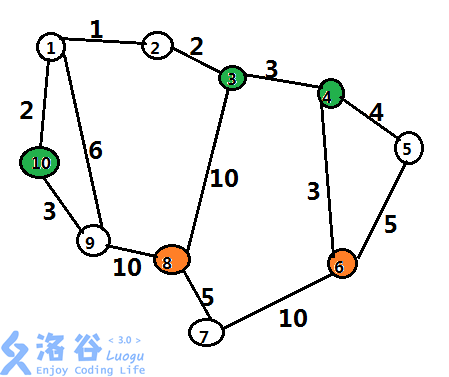
思路：数据范围$n\le50000$,所以不能使用邻接矩阵，于是使用链式前向星。根据样例一看出，可以罗恩去救金妮，哈利去拿日记；根据样例二看出，可以罗恩去拿日记，哈利去救金妮。再加上一个人单独前往的情况，于是就有了4种走法：

1. 罗恩拿日记，哈利救金妮；

2. 罗恩救金妮，哈利拿日记；

3. 哈利自己救金妮并拿日记；

4. 罗恩自己救金妮并拿日记；

这样一看要跑四遍SPFA，但是由于罗恩能走的哈利也能走，哈利能走的罗恩却不能走，所以罗恩单独前往的SPFA就可以省略了。然后求出三种走法的最小值即可。其中注意的是，当求哈利自己走时，由于先前已经求过哈利到日记和金妮的最小值了，所以只要求日记到金妮的最小值。

【代码】 ：

#include<bits/stdc++.h>
using namespace std;
int n,m,p,k=0,k1,u,v,w,x,y,lsg,b[1000000],vis[1000000];
int q[10000000],r,l,check=0,ans[1000000],c[1000000];
int zc[100];//用来存放临时答案。
struct sb {
	int u,v,w,next;
};
sb a[1000000];
void ctt(int u,int v,int w) {
	a[++k].u=u;
	a[k].v=v;
	a[k].w=w;
	a[k].next=b[u];
	b[u]=k;
	return;
}
void SPFA() {
	for(int i=1; i<=n; i++)ans[i]=1e9;
	r=0;
	l=1;
	memset(c,0,sizeof(c));//j因为有多次SPFA所以要记得及时清除。
	if(check!=2) {//当两人一起行动时,从一开始。
		q[++r]=1;
		ans[1]=0;
	}
	else {//当哈利自己行动时，只要计算从日记到金妮。
		q[++r]=x;
		ans[x]=0;
	}
	while(l<=r) {
		int u=q[l++];
		c[u]=0;
		if(!check&&vis[u])continue;/罗恩无法通过带蛇的房间。
		for(int i=b[u]; i; i=a[i].next) {
			int v=a[i].v;
			if(ans[v]>ans[u]+a[i].w) {
				ans[v]=ans[u]+a[i].w;
				if(c[v]==0) {
					c[v]=1;
					q[++r]=v;
				}
			}
		}
	}
}
int main() {
	cin>>n>>m>>k1;
	for(int i=1; i<=k1; i++) {
		cin>>lsg;
		vis[lsg]=1;//带蛇的房间打上标记。
	}
	for(int i=1; i<=m; i++) {
		cin>>u>>v>>w;
		ctt(u,v,w);
		ctt(v,u,w);
	}
	cin>>x>>y;
	SPFA();//先从罗恩开始，这样思路稍微清晰点，此时check=0。
	zc[1]=ans[x];//罗恩到金妮的路程。
	zc[2]=ans[y];//罗恩到日记的路程。
	check++;
	SPFA();//此时求哈利的路程，check=1，上面判断有蛇房间的判断已失效。
	zc[3]=ans[x];//哈利到金妮的路程。
	zc[4]=ans[y];//哈利到日记的路程。
	check++;
	SPFA();//求日记到金妮的路程，此时check=2，上方的判定生效。
	zc[5]=ans[y];//日记到金妮的路程。
	int x2,y2,z2;//三个临时存放点
	x2=max(zc[1],zc[4]);//计算罗恩救金妮，哈利拿日记的最大值，因为此时时间应是最后完成的时间，才是结束，样例二可看出。
	y2=max(zc[2],zc[3]);//计算哈利救金妮，罗恩拿日记的最小值。
	z2=min(zc[3],zc[4])+zc[5];//计算哈利自己行动的最小值，使用min因为此时一人行动，从最小开始才最优。
	x2=min(x2,y2);//比较罗恩救金妮，哈利拿日记和哈利救金妮，罗恩拿日记的最小值，x2更新为此时的最小值。
	cout<<min(x2,z2);//用上一次比较的最小值同哈利自己行动的路程比较，最小值就是最终答案。
	return 0;
}

完结撒花。