自动搬运

查看原文

来自洛谷，原作者为

	_ctz Ádigie šos ök iroг.

搬运于2025-08-24 22:05:16，当前版本为作者最后更新于2019-03-18 21:52:49，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

进入我的$blog$阅读

传送门

壮哉我大线段树！

这种毒瘤查询肯定不能在线用数据结构维护，考虑把询问离线下来处理。

假设在某个询问$[L,R]$中某种蘑菇的数量为$x$，这种蘑菇在整个序列中的数量为$all$，则区间$[L,R]$之外的蘑菇数量为$all-x$。

当$|x-(all-x)|\le k$时该种蘑菇会有$1$贡献。分类讨论解方程就有

$\dfrac{all-k}{2}\le x\le \dfrac{all+k}{2}$（由于整形精度问题，代码中的解应为$\dfrac{all-k+1}{2}\le x\le \dfrac{all+k}{2}$）

也就是说如果固定$R$，左端点只要在某个区间内就能获得这种蘑菇的贡献。

献上一张图助于理解：

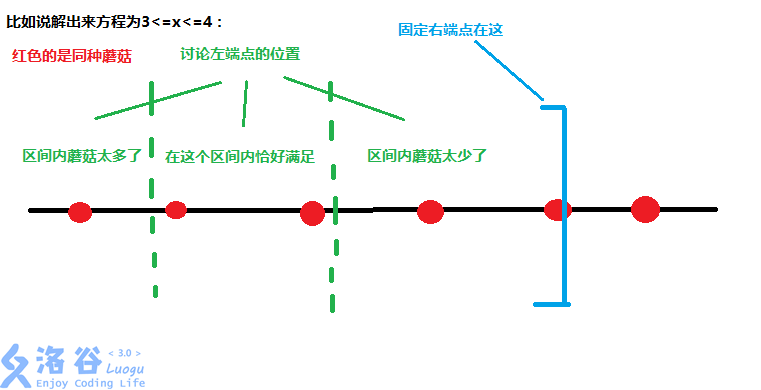
记$next[i]$为下一个和位置$i$同种的蘑菇的位置。注意到右端点移动到$next[R]$，则对应的

绿色区间$[l,r]$也会移动到$[next[l],next[r]]$上。

而一种蘑菇当前能产生贡献的的区间为 $[$ 从$R$往前数第$\dfrac{all-k+1}{2}$个同种蘑菇的位置，从$R$往前数第$\dfrac{all+k}{2}$个同种蘑菇的位置 $]$

这样把每个位置开一个$vector$，每个询问插进它右端点的$vector$中。扫一遍序列，存一下每种蘑菇当前能产生贡献的区间，每次扫到这种蘑菇就删去旧区间的贡献（区间$-1$），并更新新区间的贡献（区间$+1$）。遇到询问右端点单点查询左端点的值作为答案。

区间加减$+$单点查询，树状数组差分可以做。然而线段树作为蒟蒻的信仰，肯定要写一发线段树。既然只有单点查，所有非叶子节点也不需要维护总和，直接维护$tag$，查询时把经过的$tag$加起来就好了，不吸氧最后一个点$2100ms+$（树状数组$1500ms+$）。

代码（可能肥肠乱，因为维护的东西比较复杂。。。）：

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cmath>
#include <cstring>
#include <vector>

#define maxn 1000005
#define inf 0x3f3f3f3f

using namespace std;

inline int read(){
	int x=0,y=0;
	char ch=getchar();
	while(ch<'0'||ch>'9'){if(ch=='-')y=1;ch=getchar();}
	while(ch>='0'&&ch<='9')x=(x<<1)+(x<<3)+(ch^48),ch=getchar();
	return y?-x:x;
}
int n,k,a[maxn];
struct Question{
	int l,ans;
}q[maxn];//每个询问
struct Segment_Tree{
#define ls(x) x<<1
#define rs(x) x<<1|1
	int tag[maxn<<2];
	void add(int L,int R,int l,int r,int node,int d){
		if(L<=l&&R>=r){
			tag[node]+=d;
			return;
		}
		int mid=l+r>>1;
		if(L<=mid)add(L,R,l,mid,ls(node),d);
		if(R>mid)add(L,R,mid+1,r,rs(node),d);
	}
	int ask(int poi,int l,int r,int node){
		if(l==r)return tag[node];
		int mid=l+r>>1;
		if(poi<=mid)return ask(poi,l,mid,ls(node))+tag[node];
		else return ask(poi,mid+1,r,rs(node))+tag[node];
	}
}st;//线段树
int ll[maxn],rr[maxn],fir[maxn],nex[maxn],last[maxn],all[maxn],cnt[maxn],li[maxn];
//ll、rr就是每种蘑菇当前能产生贡献的区间
//fir是每种蘑菇第一次出现的位置，nex是前面说的next，last是每种蘑菇上一次出现的位置，用于更新nex数组
//all是每种蘑菇总出现次数，cnt是当前已经出现过了几次，li是它的区间限制
bool vis[maxn];
vector<int>Q[maxn];
inline int limit(int i){
	return max(0,(all[i]-k+1)>>1);
}
//计算区间
//其实不难发现，(all+k)/2=all-(all-k+1)/2，所以知道一边另一边直接减一下就行了
int main(){
	n=read();
	int m=read();
	k=read();
	for(register int i=1;i<=n;++i){
		a[i]=read(),++all[a[i]];
		nex[last[a[i]]]=i,last[a[i]]=i,ll[a[i]]=1;
		if(!fir[a[i]])fir[a[i]]=i;
	}
	for(register int i=n;i;--i)
		if(!nex[i])nex[i]=n+1,li[a[i]]=limit(a[i]);
	nex[n+1]=n+1;
	for(register int i=1;i<=m;++i)
		q[i].l=read(),Q[read()].push_back(i);
	int co,p,l;
	for(register int i=1;i<=n;++i){
		co=a[i],p=++cnt[co],l=li[co];
		if(rr[co])st.add(ll[co],rr[co],1,n,1,-1);
		if(p>=l){
			if(!rr[co])rr[co]=fir[co];
			else rr[co]=nex[rr[co]];
		}
		if(p>=all[co]-l+1){
			if(!vis[co])ll[co]=fir[co]+1,vis[co]=1;
			else ll[co]=nex[ll[co]-1]+1;	
		}
		if(rr[co])st.add(ll[co],rr[co],1,n,1,1);
        //上面四个if都是用来维护这个区间的，蒟蒻也不好解释清楚了。。。感性理解一下吧。。。
		for(register int j=0;j<Q[i].size();++j)
			q[Q[i][j]].ans=st.ask(q[Q[i][j]].l,1,n,1);
	}
	for(register int i=1;i<=m;++i)
		printf("%d\n",q[i].ans);
}