自动搬运

查看原文

来自洛谷，原作者为

	x_angelkawaii_x **

搬运于2025-08-24 22:05:15，当前版本为作者最后更新于2018-10-07 12:18:27，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

首先应该不难想到一维$dp$,$dp[i]$表示到第$i$个点的最大受益,对每个点$dfs$到它所有后面距离它$a,b$长度的点并更新

然而后来这样复杂度最坏是$O(n^b)$,比如下面这种图:

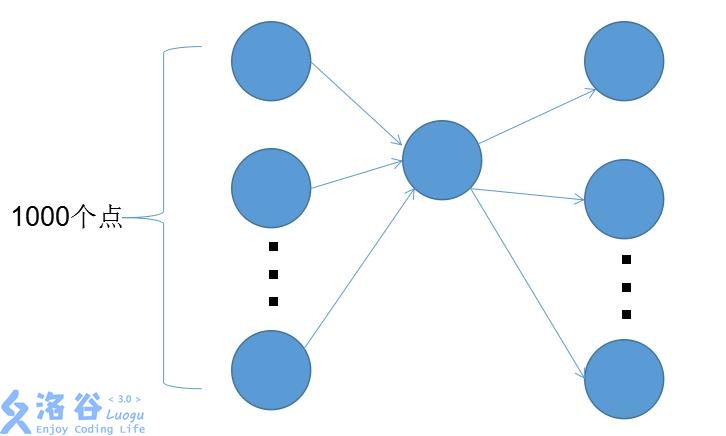
如果$b=2$那么对于左侧的每一个点,都会去更新右边的所有点,复杂度就是平方级别的,你可以试想如果这种结构重复十次然后$b=20$的复杂度

$gg$

其实做到这里$60$分也是不错的成绩了,正解是不太好想的二维$dp$,意会一下就好

$dp[i][k]$表示第$i$号点,还需要从这个点走$k$步才能停下来的最大收益

那么,先拓扑排序,对于一个点$u$,我们枚举它直接相连的点$v$,那么转移有四种:

$$dp[v][i]=max(dp[v][i],dp[u][i+1])(0<i<b)$$ $$dp[v][a-1]=max(dp[v][a-1],dp[u][0]-w_a)$$ $$dp[v][b-1]=max(dp[v][b-1],dp[u][0]-w_b)$$ $$dp[v][0]=max(dp[v][0],dp[u][1]+w[v])$$($w[i]$表示$i$处收益) 然后就可以愉快的水过了(雾),注意$dp[1][0]$的初值 难度主要集中在思维难度上 $ACcode$ ```cpp struct edge { int to,next; }e[maxn<<4]; int head[maxn],cnt=0; int f[maxn][51]; int rudu[maxn]; int w[maxn]; inline void addedge(int u,int v) { e[++cnt].to=v,e[cnt].next=head[u],head[u]=cnt; } queueq; void del(int x) { for(int i=head[x];i;i=e[i].next) { int v=e[i].to; rudu[v]--; if(!rudu[v]&&v!=1)q.push(v); } } int main() { scanf("%d%d%d%d%d%d%d",&n,&m,&k,&a,&b,&wa,&wb); int u,v; for(int i=1;i<=n;++i)u=read(),v=read(),w[u]+=v; for(int i=1;i<=k;++i)u=read(),v=read(),addedge(u,v),rudu[v]++; memset(f,-127,sizeof(f)); for(int i=2;i<=m;++i) if(!rudu[i])q.push(i); while(!q.empty()) { int u=q.front();q.pop(); del(u); } q.push(1); f[1][0]=w[1]; while(!q.empty()) { int x=q.front();q.pop(); del(x); for(int i=head[x];i;i=e[i].next) { int v=e[i].to; if(f[x][0]!=f[0][0]) { if(a!=1)f[v][a-1]=max(f[v][a-1],f[x][0]-wa); else f[v][0]=max(f[v][0],f[x][0]-wa+w[v]); } if(f[x][0]!=f[0][0]) { if(b!=1)f[v][b-1]=max(f[v][b-1],f[x][0]-wb); else f[v][0]=max(f[v][0],f[x][0]-wb+w[v]); } if(f[x][1]!=f[0][0])f[v][0]=max(f[v][0],f[x][1]+w[v]); for(int j=b;j>1;--j) if(f[x][j]!=f[0][0])f[v][j-1]=max(f[v][j-1],f[x][j]); } } int ans=0; for(int i=1;i<=m;++i)ans=max(ans,f[i][0]); printf("%d\n",ans); } ```$$