1 条题解
-
0
自动搬运
来自洛谷,原作者为

Chinese_zjc_
发生肾么事了?搬运于
2025-08-24 22:05:13,当前版本为作者最后更新于2020-09-03 18:55:41,作者可能在搬运后再次修改,您可在原文处查看最新版自动搬运只会搬运当前题目点赞数最高的题解,您可前往洛谷题解查看更多
以下是正文
先看下面这张图:
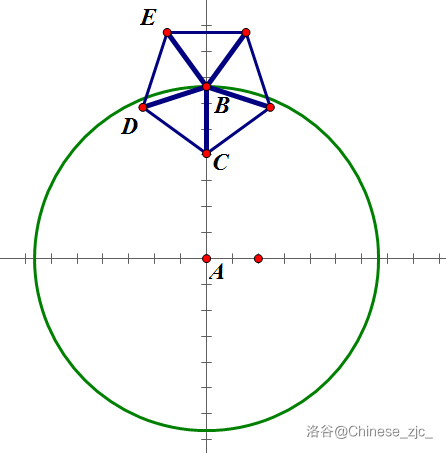
绕 顺时针旋转的时候, , , 等点也随着 一起旋转.
从题目配图中显然可以看出, , , , , 五点之间的相对位置不会改变.
那我们直接可以把 , 这些量忽略掉,于是这道题目就成了静态.
而且由于正五边形存在对称轴,因此只需要考虑 个点 , , 能否攻击到 .
我们设 , 在 轴上.
易得: , ,正五边形关于 轴对称.
然后我们来求 和 的坐标.
作 交于点 , 交于点 , 交于点 .
如图:
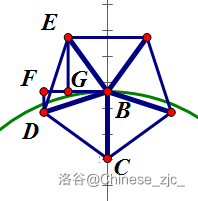
则易得 , .
再使用三角函数,即得: $ D:(-\cos(18^\circ)\times r,R-\sin(18^\circ)\times r) $ , $ E:(-\cos(54^\circ)\times r,R+\sin(54^\circ)\times r) $ .
再考虑子弹方向:
对于 和 第一个子弹的方向分别是射线 和射线 .
对于第 个子弹,相对于第 个子弹顺时针旋转了 .
因此若 或 要射到 , 或 必须得是 的倍数.
让我们求出 和 的度数.
依然是三角函数:
$$\angle AEG=\arctan(\frac{\cos(18^\circ)\times r}{R-\sin(18^\circ)\times r})\\ \angle AFD=\arctan(\frac{\cos(54^\circ)\times r}{R+\sin(54^\circ)\times r})\\ $$这样,直接计算判断即可,而 射到 的情况显然当且仅当 为偶数.
那我们就可以愉快地写代码了.
:
//This Code was made by Chinese_zjc_. #include<cstdio> #include<cmath> #define int long long #define PI 3.14159265358979323 #define EQUAL 0.00000000000001 #define double long double using namespace std; int T,k; double r,R,v,t,siz[5],atime; bool answered; double _360topi(const double IN) { return IN/180*PI; } signed main() { scanf("%lld",&T); while(T--) { scanf("%Lf%Lf%Lf%Lf%lld",&r,&R,&v,&t,&k); answered=false; if(!(k&1)) { puts("no"); continue; } siz[1]=_360topi(180)-atan((cos(_360topi(18))*r)/(R-sin(_360topi(18))*r)); siz[2]=_360topi(180)-atan((cos(_360topi(54))*r)/(R+sin(_360topi(54))*r)); atime=PI*2/k; for(int i=1;i<=2;++i) { int tim=siz[i]/atime+EQUAL; if(abs(tim*atime-siz[i])<EQUAL) { puts("no"); answered=true; break; } } if(!answered) { puts("yes"); } } return 0; }回头看到式 ,这就不禁让人想问了:
是不是它们都是无理数?
这是显然的,证明略.
那我们就可以拿出我们在二年级就学过的知识:
无理数除以一个有理数的结果必定为无理数.
很显然,因此证明略.
那代码可以进行简化:
:
//This Code was made by Chinese_zjc_. #include<cstdio> using namespace std; int T,k; double r,R,v,t; signed main() { scanf("%lld",&T); while(T--) { scanf("%lf%lf%lf%lf%lld",&r,&R,&v,&t,&k); puts(k&1?"yes":"no"); } return 0; }
- 1
信息
- ID
- 3799
- 时间
- 500ms
- 内存
- 125MiB
- 难度
- 3
- 标签
- 递交数
- 0
- 已通过
- 0
- 上传者
