自动搬运

查看原文

来自洛谷，原作者为

	LHF qwq

搬运于2025-08-24 22:05:03，当前版本为作者最后更新于2019-11-14 18:21:41，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

终于AC这一题了，发个题解庆祝一下吧！！！

首先，大家要先用Dinic或ISAP做对【模板】网络最大流（不会网络最大流的可以点这里），根据推断，网络最大流=网络最小割。

首先，我们要知道。按照正常暴力的算法，这一题会被T飞的。为了防止TLE事件不再发生。我们就要采取相应的优化措施。

怎么弄？其实也不难。我们可以建立一棵最小割树。 （最小割树？啥？）

最小割树=分治+最小割（最大流）

其实，我们可以这样做：

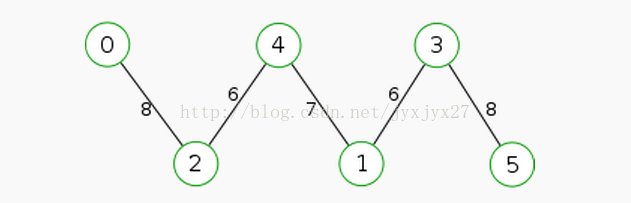
先建立一个无向图，然后再把这个图的整体看做一个集合，然后任意选择两个点（设它们为1和5），在原图上跑一趟最小割。如图：

然后，因为1和5已经无法连接了，所以我们可以把1和5再分成两个集合，中间由一条边连接，这条边的权值为两点之间的最小割。然后，我们再对每个集合进行这样的操作（注意，最小割要在原图上跑），再分下去，直到集合内只剩一个节点为止。如图：

最后，我们可以得到一棵最小割树。

这里要注意，跑最小割（最大流）要在原图上跑！！！

大功告成(〃'▽'〃)，这棵树中任意两点的最小割等于原图上任意两点的最小割，因此，我们直接用BFS来查找就行了，查找一个的时间复杂度是O(n)，这样求Q个最小割只需要用O(Qn)的时间复杂度，查询代码如下：

int findans()
{
	head=0,tail=1;
	d[head]=a;
	for(register int i=0;i<=n;i++) dis[i]=0;
	dis[a]=0x7ffffff;
	while(head<tail)
	{
		t=d[head];
		head++;
		for(register int i=trf[t];i;i=tr[i].next)
		{
			if(dis[trar]==0)
			{
				dis[trar]=min(dis[t],tr[i].flow+1);
				if(trar==b) return dis[b]-1;
				d[tail]=trar;
				tail++;
			}
		}
	}
	return dis[b]-1;
}

然后就是如何构建这一棵树。其实也不难，因为Dinic或ISAP跑dfs时图中有一些边的容量为0，其实就代表要割掉那一条边，所以我们只需要用搜索的方式来寻找两个集合中分别包含那些数，代码如下：

void build(int l,int r)
{
	if(l>=r)return;
	//在原图上跑两点之间的最小割
	a=v[l];
	b=v[l+1];
	dinic();
	//给两个集合之间加一条无向边
	adtr(a,b,ans);
	adtr(b,a,ans);
	//寻找两个集合的元素
	int tl1=0,tl2=0;
	for(register int i=l;i<=r;i++)
	{
		if(dis[v[i]])
		{
			tl1++;
			t1[tl1]=v[i];
		}
		else
		{
			tl2++;
			t2[tl2]=v[i];
		}
	}
	for(register int i=1;i<=tl1;i++) v[i+l-1]=t1[i];
	for(register int i=1;i<=tl2;i++) v[l+tl1+i-1]=t2[i];
	//分治下去
	build(l,tl1+l-1);
	build(l+tl1,r);
}

好了，最后来一份完整代码:

#pragma GCC optimize(3)
#include<cstdio>
#define N 100010
#define kar k[i].ar
#define trar tr[i].ar
#define min(a,b) (a<b?a:b)
using namespace std;
int a,b,t,n,m,f[N],ans,trl;
struct node {
	int next,ar,flow;
} k[N*20],tr[N*20];
int trf[N],ss;
int first[N],dis[N],len;
int x[N],y[N],v[N],e[N];
int t1[N],t2[N],tl1,tl2;
void add(int a,int b,int t) {
	len++;
	k[len].ar=b;
	k[len].next=first[a];
	first[a]=len;
	k[len].flow=t;
}
void adtr(int a,int b,int t) {
	trl++;
	tr[trl].ar=b;
	tr[trl].next=trf[a];
	trf[a]=trl;
	tr[trl].flow=t;
}
int head,tail,d[N];
bool bfs() {
	head=0,tail=1;
	d[0]=a;
	for(register int i=0; i<=n; i++) dis[i]=0;
	dis[a]=1;
	while(head<tail) {
		t=d[head];
		head++;
		for(register int i=first[t]; i; i=k[i].next) {
			if(dis[kar]==0&&k[i].flow>0) {
				dis[kar]=dis[t]+1;
				if(kar==b) return true;
				d[tail]=kar;
				tail++;
			}
		}
	}
	return false;
}
int dfs(int xx,int flow) {
	if(xx==b) return flow;
	if(flow==0) return 0;
	if(dis[xx]>=dis[b])return 0;
	int h,s=0;
	for(register int i=first[xx]; i>1; i=k[i].next) {
		if(flow==0) {
			dis[xx]=0;
			break;
		}
		if(dis[kar]==dis[xx]+1&&k[i].flow>0) {
			h=dfs(kar,min(flow,k[i].flow));
			s+=h;
			flow-=h;
			k[i].flow-=h;
			k[i^1].flow+=h;
			if(h==0) dis[kar]=0;
		}
	}
	return s;
}
void dinic() {
	for(register int i=0; i<=n; i++) {
		dis[i]=0;
		first[i]=0;
	}
	len=1,ans=0;
	for(register int i=1; i<=m; i++)
		add(x[i],y[i],f[i]),add(y[i],x[i],f[i]);
	while(bfs()) ans+=dfs(a,0x7ffffff);
}
void build(int l,int r) {
	if(l>=r)return;
	a=v[l];
	b=v[l+1];
	dinic();
	adtr(a,b,ans);
	adtr(b,a,ans);
	int tl1=0,tl2=0;
	for(register int i=l; i<=r; i++) {
		if(dis[v[i]]) tl1++,t1[tl1]=v[i];
		else tl2++,t2[tl2]=v[i];
	}
	for(register int i=1; i<=tl1; i++) v[i+l-1]=t1[i];
	for(register int i=1; i<=tl2; i++) v[l+tl1+i-1]=t2[i];
	build(l,tl1+l-1);
	build(l+tl1,r);
}
int findans() {
	head=0,tail=1;
	d[head]=a;
	for(register int i=0; i<=n; i++) dis[i]=0;
	dis[a]=0x7ffffff;
	while(head<tail) {
		t=d[head];
		head++;
		for(register int i=trf[t]; i; i=tr[i].next) {
			if(dis[trar]==0) {
				dis[trar]=min(dis[t],tr[i].flow+1);
				if(trar==b) return dis[b]-1;
				d[tail]=trar;
				tail++;
			}
		}
	}
	return dis[b]-1;
}
int main() {
	int T;
	len=1;
	scanf("%d%d",&n,&m);
	for(register int i=1; i<=m; i++) {
		scanf("%d%d%d",&a,&b,&t);
		x[i]=a,y[i]=b,f[i]=t;
	}
	for(register int i=0; i<=n; i++) v[i]=i;
	build(0,n);
	scanf("%d",&T);
	while(T--) {
		scanf("%d%d",&a,&b);
		printf("%d\n",findans());
	}
	return 0;
}

好了，到此结束了（逃）。