自动搬运

查看原文

来自洛谷，原作者为

	WeLikeStudying 

搬运于2025-08-24 22:05:01，当前版本为作者最后更新于2021-12-20 20:23:20，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

• 题目说得一点都不清楚（可能是因为它是从某 $\text{OJ}$ 搞过来的吧，那为啥不把那充满文采的题目背景也搬过来呢）。
• 作者结合原 $\text{OJ}$ 的文案再次对题面进行了改造。

题意是啥

• 原题链接。
• 给定一棵 $n$ 个节点的无根树，对该树的节点进行黑白染色，要求任意两个黑点没有直接的边相连，求本质不同的染色方案模 $10^9+7$ 的余数。
• 如果两个染色方案所形成的树可以对节点重新标号后，使得对于任意编号为 $u$ 的节点，它在两棵树中只会同时为黑色或同时为白色，而且任意边 $(u,v)$ 在两棵树中只会同时存在或同时不存在，则称两个染色方案相同（说白了两个方案的树同构）。
• $n\le 5\times 10^5$。
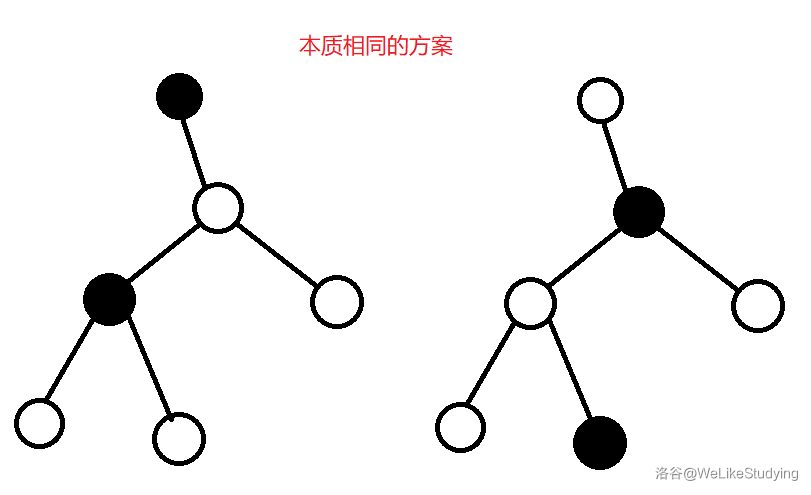
• 作者一开始根本不明白题目在讲什么，而唯一的题解……额，总之作者将围绕自己遇到的问题开始讲解。

最开始的思路怎么来的

• 看起来很像树论的树形计数动态规划对吧，但是树是无根的。
• 我们如果直接强行选定一个根的话，就可能出现这样一种情况：比如选定 $u$ 为根，可能存在节点 $v$ 满足 $u\ne v$ 使得以 $u$ 为根的有根树和以 $v$ 为根的有根树同构，那样方案明显会算重复。
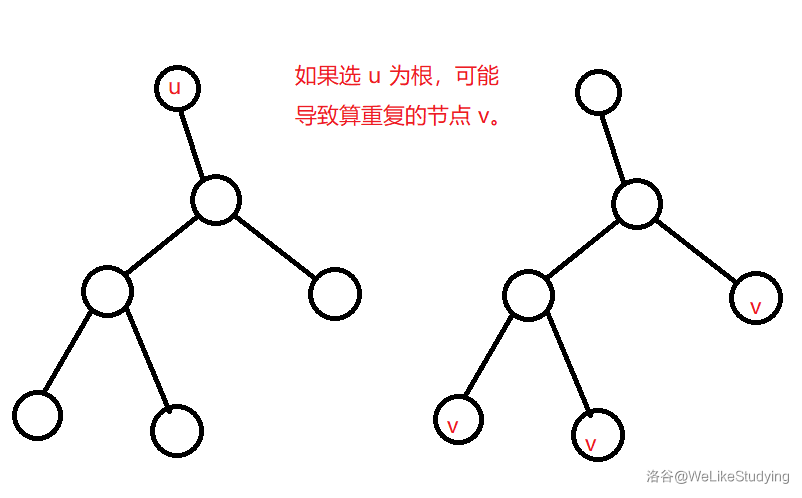
• 尽管我们还未确定具体的策略，但强后效性是不允许的。
• 有没有好的办法来避免这一问题呢。
• 我们知道，一棵树的重心与这棵树的根是哪个没有关系，我们可以尝试以重心为根。
• 那么重心为啥不可替代呢：因为如果有 $u,v$，$u$ 是重心，以 $u,v$ 为根的树同构，那它们最大子树相等，那么 $v$ 也是重心，所以不用担心算重复。
• 请保证理解这些知识：一棵树最多有两个重心，如果有两个重心，那么这两个重心一定直接连边。
• 接下来我们重点讲解只有一个重心的情况，最后再解析如何求解有两个重心的问题。

如何计算方案数

• 我们已经在实质上将无根树转化为有根树进行求解了，接下来问题就在于计算方案数。
• 首先可以很套路地设出 $f(u,0/1)$ 表示以 $u$ 为根（$u$ 是否染成黑色）的子树的染色方案数，转移比较基本。
• 接下来遇到一个很严重的问题：$u$ 可能有很多个不同的子树，这些子树如果两两不同构那当然好处理，但如果有同构的怎么办？（先忽略我们还不知道树同构如何判断的事实）
• 打个比方，我知道有 $m$ 棵同构的树，它们的方案数都是 $n$，那么它们对 $u$ 的贡献是多少。
• 转化为一个简单的问题：$n$ 个物品中取 $m$ 个（可以取重复）的总方案数是多少？考虑在 $m$ 个物品中间插入 $m-1$ 个防止取走重复，总方案数为 $C(n+m-1,m)$。
• 接下来作者将解析如何判断树是否同构。

哈希判断树同构

• 作者知道有很多判断树同构的哈希方法，但作者介绍的方法有这样的特点：哈希只是一个辅助手段，如果没有哈希方法，对于一棵节点数为 $n$ 的有根树，构造它的复杂度是 $O(\frac{n^2\lg n}{\omega})$ 级别的，但最后会得到一个 $100\%$ 正确的判断树同构的编码。
• 理由很简单：作者希望自己的哈希通过随便更改模数的方法就可以避免针对，而不是寄希望于数据多水。
• 作者的哈希值以 $01$ 串的形式编码。
• 方法很简单：叶节点的哈希值为 $H(u)=01$。
• 对于节点 $u$，节点按照哈希值字典序大小排序（由于要求本质相同所以要排序），编码为 $v_1,v_2,\cdots v_m$，那么有：

• 可以轻易地将其当作二进制整数进行编码，下面是一个例子：
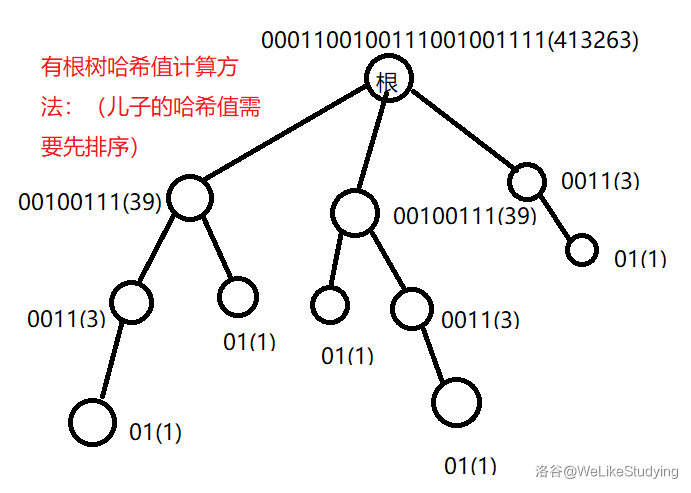
• 通过这样的方式，即可用 $O(n\lg n)$ 的时间，算出树上每个节点的哈希值，并以哈希值的相等与否来比较子树的同构与否。
• 编码时可以同时计算子树大小和答案，起到辅助哈希的效果。

有两个重心的情况

• 有两个重心怎么办？
• 如果有两个重心，那么这两个重心一定直接连边。
• 断开这条边，变成两个子树（显然相当于有根），分情况讨论就好了：
• 分析如果两棵子树同构应该怎么办，如果不同构应该怎么办，已经不是最困难的部分了。

代码实现

• 代码实现。
• 作者是 $1A$ 的，思路稳当，打得自然顺畅。
• 这里作者记一下代码细节，如果您实现出现问题的话也可以看看。
• 一定要在深度优先搜索之后记录搜索的节点，不然会被覆盖。
• 记录的节点要套一个数组，不要直接写下标。