自动搬运

查看原文

来自洛谷，原作者为

	ez_lcw **

搬运于2025-08-24 22:04:30，当前版本为作者最后更新于2020-08-11 13:58:19，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

上下界网络流的做法大佬们都讲过了，我就来讲一个另类的解法。（不过也是网络流）

这个做法是考场上想了很久都不会后奇思妙想想出来的（不会上下界网络流），所以没多少思路引导。

首先原题明显可以转移成一个类似最小链覆盖的问题。

剩下的就是我的具体做法：

我们对原来的有向无环图进行改造：

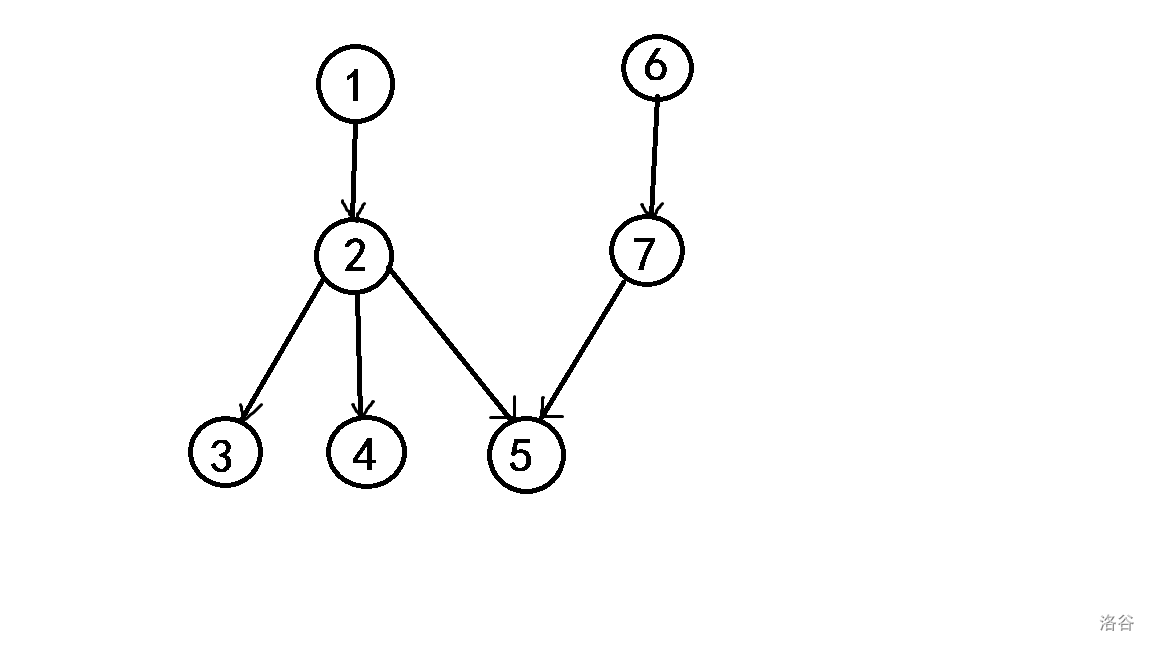
上面的是原图，我们把图中的每一条边 $e_i$ 拆成两条边：一条流量为 $1$，费用为 $1$，不妨取名叫 $a_i$；一条流量为 $\infty$，费用为 $0$，取名叫 $b_i$。然后源点向每个入度为 $0$ 的点（也就是链覆盖的起点）连边，流量 $\infty$，费用 $0$；每个出度为 $0$ 的点（也就是链覆盖的终点）向汇点连边，流量 $\infty$，费用 $0$。

然后跑最大费用最大流。

意思就是说每次增广时，相当于我新覆盖一条链。在增广中：

如果某条原图中的边 $e_i$ 没有被走过，那么为了满足最大费用，程序肯定会选择流费用为 $1$ 的那条边 $a_i$，费用增加 $1$，代表我新清理了一条雪道，即新访问了一条原图中的边；

如果这条边 $e_i$ 被走过了，那么费用为 $1$ 的那条边肯定被流满了，只能流费用为 $0$ 的边，不贡献费用，意思就是我走过的这条边在我前几次覆盖时已经被覆盖了，也就是说我只是路过这，并不要清理这。

然后根据最大费用最大流的特性，每次增广完后，能保证所得的解是当前的最优解，也就是说它能保证用最优方法覆盖所有边。

那么当贡献的费用等于总边数时，整个图也就被我们覆盖完了，答案就是链的条数，也就是覆盖的次数，或者说增广的次数。

整道题也就结束了。

顺带说一下，其实这种跑网络流却不跑完，把网络流当成一个类似贪心的工具来使用的 trick 挺实用也挺常见的（类似数学中的设而不求），比如 BZOJ2893征服王 也可以用这个 trick 做，而且比这个麻烦一点，所以建议总结一下（

代码如下：

#include<bits/stdc++.h>

#define N 110
#define M 10010
#define INF 0x7fffffff

using namespace std;

inline int read()
{
	int x=0,f=1;
	char ch=getchar();
	while(ch<'0'||ch>'9')
	{
		if(ch=='-') f=-1;
		ch=getchar();
	}
	while(ch>='0'&&ch<='9')
	{
		x=(x<<1)+(x<<3)+(ch^'0');
		ch=getchar();
	}
	return x*f;
}

int n,s,t,tot,ans;
int rudu[N],chudu[N];
int cnt=1,head[N],to[N*4+M*4],nxt[N*4+M*4],c[N*4+M*4],w[N*4+M*4];
int pre[N],dis[N];
bool inq[N];

queue<int>q;

void adde(int u,int v,int ci,int wi)
{
	to[++cnt]=v;
	c[cnt]=ci;
	w[cnt]=wi;
	nxt[cnt]=head[u];
	head[u]=cnt;
	
	to[++cnt]=u;
	c[cnt]=0;
	w[cnt]=-wi;
	nxt[cnt]=head[v];
	head[v]=cnt;
}

bool SPFA()
{
	memset(dis,128,sizeof(dis));
	q.push(s);
	dis[s]=0;
	inq[s]=1;
	while(!q.empty())
	{
		int u=q.front();
		q.pop();
		inq[u]=0;
		for(int i=head[u];i;i=nxt[i])
		{
			int v=to[i];
			if(c[i]&&dis[u]+w[i]>dis[v])
			{
				dis[v]=dis[u]+w[i];
				pre[v]=i;
				if(!inq[v])
				{
					inq[v]=1;
					q.push(v);
				}
			}
		}
	}
	return dis[t]!=dis[0];
}

void MCMF()
{
	int maxcost=0,maxflow=0;
	while(SPFA())
	{
		int minflow=INF;
		for(int u=t;u!=s;u=to[pre[u]^1]) 
			minflow=min(minflow,c[pre[u]]);
		for(int u=t;u!=s;u=to[pre[u]^1])
		{
			c[pre[u]]-=minflow;
			c[pre[u]^1]+=minflow;
			maxcost+=minflow*w[pre[u]];
		}
		maxflow+=minflow;
		ans++;//统计增广次数（链的条数）
		if(maxcost==tot) break;//如果最大费用达到总边数
	}
}

int main()
{
	n=read();
	s=1,t=1+n+1;
	for(int i=1;i<=n;i++)
	{
		int m=read();
		tot+=m;
		for(int j=1;j<=m;j++)
		{
			int v=read();
			adde(1+i,1+v,1,1);//ai
			adde(1+i,1+v,INF,0);//bi
			chudu[i]++,rudu[v]++;
		}
	}
	for(int i=1;i<=n;i++)
	{
		if(!rudu[i]) adde(s,1+i,INF,0);//源点连入度为0的点
		if(!chudu[i]) adde(1+i,t,INF,0);//出度为0的点连汇点
	}
	MCMF();//最大费用最大流
	printf("%d\n",ans);
	return 0;
}
/*
5
1 2
0
2 2 4
0
1 4
*/