自动搬运

查看原文

来自洛谷，原作者为

	chenly8128 God helps those who help themselves.

搬运于2025-08-24 22:04:26，当前版本为作者最后更新于2025-06-06 19:15:27，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

本题解复杂度为 $O(n^2 \log n)$，但在水得没边的数据下跑不过 $O(n^3)$，特此说明。希望管理大大早日加强数据。

题目分析

题目要求「使得上同一堂课的学生之间印象最坏的最好」。那么我们根据套路，可以二分答案。

设目前答案为 $x$。我们需要做的就是验证所有人的最后 $n-x-1$ 个印象，是否能一个都不出现在该同学的班级里。

注意到总共 3 个班，但是除去去年的选择，每人只剩下了两个选择，结合限制条件，于是这就是很经典的 2-sat 问题。

解决该问题可以拆分为 2 步：

1. 根据目前的二分结果下的限制条件建有向图。
2. tarjan 算法求解强连通分量，验证是否合法。

建图

设目前需要验证的答案为 $x$，有用的限制条件为每人的最后 $n-x-1$ 条，其中的人顺序不分先后。

假设有 $a$ 和 $b$ 两个学生，他们中，至少有一方在另一方的最后 $n-x+1$ 个印象中。

显然，两个学生必然拥有至少一个能一起上的课程，如图。

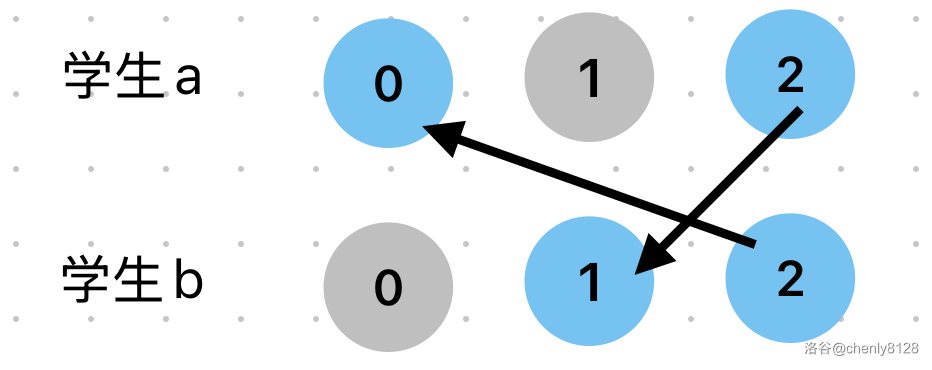
图中，两个学生都能够上课程 2。如果学生 a 选择了课程 2，那么学生 b 就一定不能选择课程 2。对于 b 来说，课程 1 和 课程 2 是对立事件，有且仅有一项成立，所以不选 2 就只能选 1。因此我们可以给 a 的课程 2 选项连一条有向边到 b 的课程 1，象征着 a 选课程 2 能够推出 b 选课程 1。

同理，我们还需要给 b 的课程 2 选项连一条有向边到 a 的课程 0。

通过这样的方法，我们就能完成建图。

tarjan

建完图就是标准的 2-sat 求解，直接对每一个节点跑 $tarjan$，给强连通块涂相同颜色。如果一个学生能选择的两个课程在同一个强连通分量里，那就说明选择其一必定得选择另一，这很明显是有问题的，直接判断不可能。

如果每一个学生都没有出现这样的情况，那么就是可能的。

代码实现

二分 $O(\log n)$ 次，每次需要重新建图 $O(n^2)$，并强连通分量缩点 $O(n+m)$。这里的 $m$ 表示边数，最坏情况下与 $n^2$ 同阶。所以总时间复杂度 $O(n^2 \log n)$，可过本题。

// Author: chenly8128
// Created: 2025-06-05 21:39:29

#include <bits/stdc++.h>
using namespace std;
const int MAXN = 1000+10;
int n,x,ne[MAXN][MAXN];
int id[MAXN][3];
int dfn[MAXN<<1],col[MAXN<<1],low[MAXN<<1];
int col_cnt,dfn_cnt;
stack <int> s;
vector <int> g[MAXN<<1];
void init (void) {
	memset (dfn,0,sizeof (dfn));
	memset (col,0,sizeof (col));
	memset (low,0,sizeof (low));
	for (int i = 1;i <= 2*n;i++) g[i].clear();
	dfn_cnt = col_cnt = 0;
}
void build (int x) {
	for (int i = 1;i <= n;i++)
		for (int j = x+1;j < n;j++) {
			int v = ne[i][j];
			for (int t = 0;t < 3;t++)
				if (id[i][t] && id[v][t]) {
					g[id[i][t]].push_back(id[v][0]+id[v][1]+id[v][2]-id[v][t]);
					g[id[v][t]].push_back(id[i][0]+id[i][1]+id[i][2]-id[i][t]);
				}
		}
}
void tarjan (int x) {
	low[x] = dfn[x] = ++dfn_cnt;
	s.push(x);
	for (int y : g[x]) {
		if (!dfn[y]) {
			tarjan(y);
			low[x] = min(low[x],low[y]);
		}
		else if (!col[y]) low[x] = min(dfn[y],low[x]);
	}
	if (low[x] == dfn[x]) {
		col_cnt++;
		while (s.top() != x) {
			col[s.top()] = col_cnt;
			s.pop();
		}
		col[x] = col_cnt; s.pop();
	}
}
bool check (int x) {
	init();
	build(x);
	for (int i = 1;i <= 2*n;i++)
		if (!dfn[i]) tarjan(i);
	for (int i = 1;i <= n;i++)
		if (col[i] == col[i+n]) return false;
	return true;
}
int main (void) {
	ios::sync_with_stdio(false);
	cin >> n;
	for (int i = 1;i <= n;i++) {
		cin >> x;
		int cur = i;
		for (int t = 0;t < 3;t++)
			if (x == t) id[i][t] = 0;
			else {
				id[i][t] = cur;
				cur += n;
			}
		for (int j = 1;j < n;j++) cin >> ne[i][j];
	}
	int l = 0,r = n-1;
	while (l < r) {
		int mid = (l + r) >> 1;
		if (check (mid)) r = mid;
		else l = mid+1;
	}
	cout << r << '\n';
	return 0;
}