自动搬运

查看原文

来自洛谷，原作者为

	Isprime 总有一天他们会讲述你的传奇

搬运于2025-08-24 22:04:18，当前版本为作者最后更新于2019-10-05 11:24:21，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

题解P4822[BJWC2012]冻结

配合Blog食用更佳

原题传送门

分层图模板题

题意简化：有n个点，m条边，求s到t的最短路

现在让我们口胡一张图，是这样的（图很丑，请见谅）

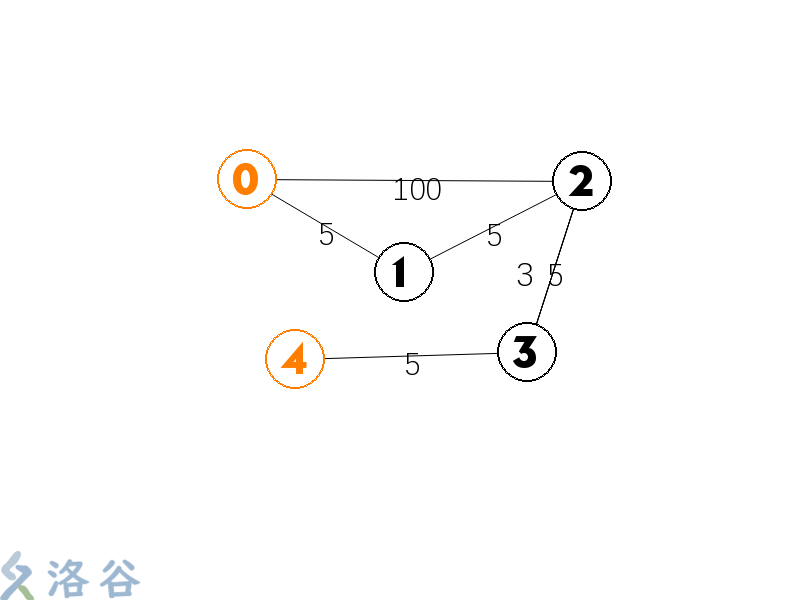
但题目中多了一个条件：我们至多可以让k条边的权值变为原来的50%（不一定要有k条边权值变成50%）

这不就是分层图裸题吗，建k层图（因为k≤50，所以并不会占用太大的空间），举个栗子：x和y之间有一条权值为z的边，则第0到k层的x,y之间都要连权值为z的边,第0到k-1层的x或y连到第i+1层的y或x的权值改为原来的50%

图就变成了下面这个样子↓

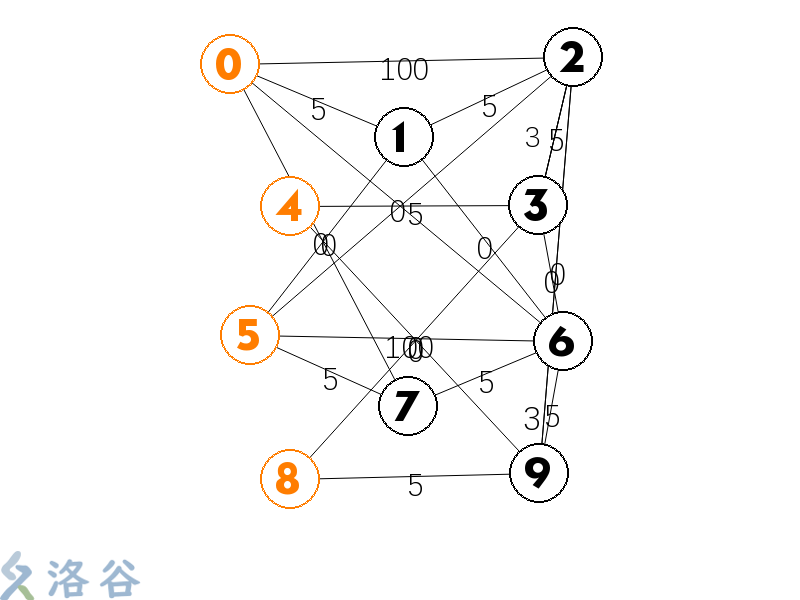
乱七八糟，看都看不清

图里面有一些0，你就当成是原来的50%吧毕竟画图的那个软件不知道被我丢哪儿去了

p.s.图中8和9的编号画反了 ，凑合着看吧

好吧等有时间了我会改

所以最终答案只需要跑一边Dijkstra再找出dis[i*(n+1)+t]的最小值即为答案

Code

#include<cstdio>
#include<queue>
#define ri register int
#define MAXN 51
#define MAXM 1001 
#define INF 2147483647
using namespace std;
int n,m,k,edge_sum;
int head[MAXM*201],dis[MAXN*201];
bool vis[MAXN*201];
struct Edge{
	int next,to,dis;
}edge[MAXM*201];
inline void addedge(int from,int to,int dis){
	edge[++edge_sum].next=head[from];
	edge[edge_sum].dis=dis;
	edge[edge_sum].to=to;
	head[from]=edge_sum;
}
struct Node{
	int u,dis;
	bool operator <(const Node& rhs) const {
        return dis>rhs.dis;
    }
};
inline void dijkstra(){
	priority_queue<Node> q;
	q.push((Node){1,0});
	while(!q.empty()) {
		int u=q.top().u;
		q.pop();
		vis[u]=1;
		for(ri i=head[u];i;i=edge[i].next)
			if(!vis[edge[i].to]&&dis[edge[i].to]>dis[u]+edge[i].dis){
				dis[edge[i].to]=dis[u]+edge[i].dis;		
				q.push((Node){edge[i].to,dis[edge[i].to]});
			}
	}
}
int main()
{
	scanf("%d %d %d",&n,&m,&k);
    for(ri i=1;i<=m;i++)
    {
    	int x,y,z;
        scanf("%d%d%d",&x,&y,&z);
        for(ri j=0;j<=k;j++) addedge(j*n+x,j*n+y,z),addedge(j*n+y,j*n+x,z);
        for(ri j=0;j<k;j++) addedge(j*n+x,(j+1)*n+y,z/2),addedge(j*n+y,(j+1)*n+x,z/2);
    }
    for(ri i=1;i<=n*k+n;i++) dis[i]=INF;
    dis[1]=0;
    dijkstra();
    int min=INF;
    for(ri i=0;i<=k;i++) if(min>dis[i*n+n]) min=dis[i*n+n];
    printf("%d\n",min);
    return 0;
}
}

码风真差

说句闲话：研究分层图的最好方法是

A了4568,再A了2939，还要A了4822

祝你们成功 (滑稽

3倍经验

我都告诉你这么多了，不点个赞？