自动搬运

查看原文

来自洛谷，原作者为

	SDNetFriend 路漫漫其修远兮，吾将上下而求索 | AFO

搬运于2025-08-24 22:03:44，当前版本为作者最后更新于2022-03-22 16:24:39，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

这个题用的是切比雪夫距离，我们知道在格点图上，到一个点切比雪夫距离相等的点形成了一个矩形的环。

看数据范围，$W\times H\leq 2.5\times 10^6$ 意味着我们可以开一个二维数组保存下每一个格子的答案。

刚开始可能会想扫描线，但是这样还是比较麻烦，我们换一种思路，尝试预先求出每个点的辐射量然后直接二维前缀和 $O(1)$ 回答每个询问。。

我们都知道二维平面上的矩形加用差分怎么做，但这个题不止是一个矩形加，对于一个核电站的贡献，可以被描述成 $O(W)$ 个矩形加，大概长成这样：

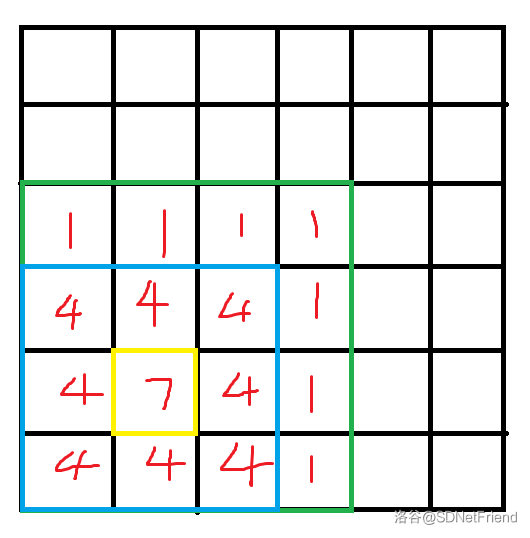
如图，是一个对应输入为 2 2 7 3 的矩形。我们以左右方向为 $x$ 轴，上下为 $y$ 轴且左下角为原点。

考虑我们怎么来计算这个东西？我们不妨尝试画出一个更简单的例子的差分数组，对应着核电站 3 3 6 2：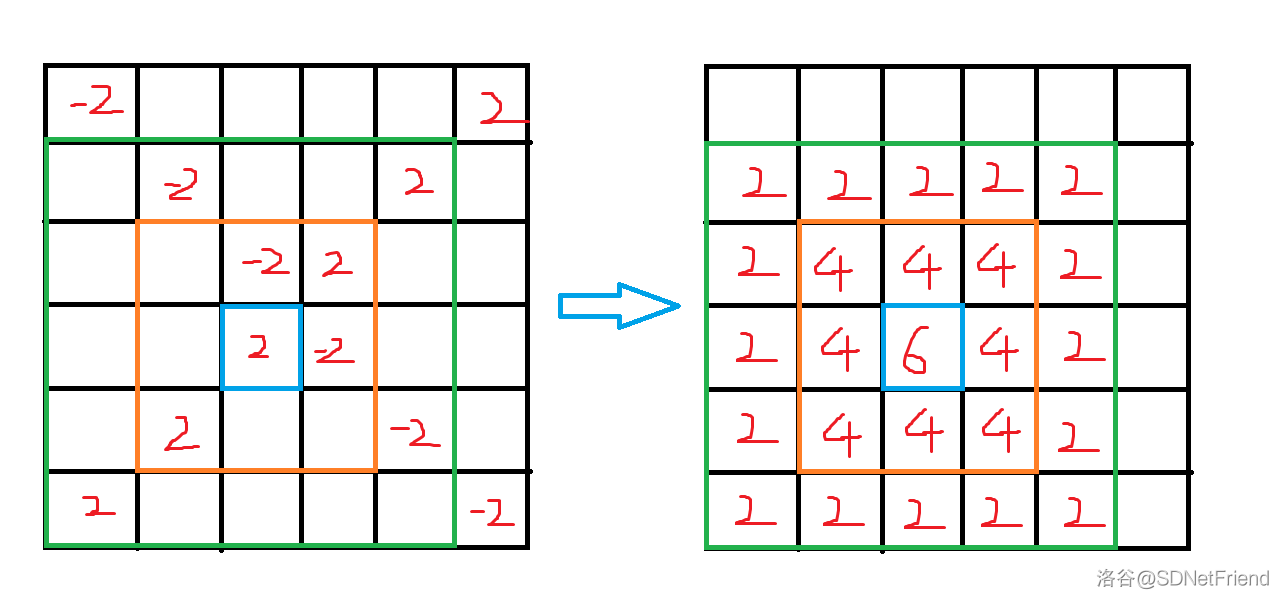

左侧是差分数组，右侧是最终每个点的辐射值。

我们发现，差分数组可以被描述成两条斜线，一条方向与主对角线相同，另一条方向与主对角线垂直。

那我们考虑，做一个差分数组的差分，存成两个数组，一个数组差分方向是左下到右上，另一个数组差分方向是右下到左上，最后对这两个数组做前缀和我们就得到了差分数组。然后再次前缀和就能得到每个位置的辐射值，再次前缀和就可以直接二位前缀和回答询问了。

做到这里我们只能获得 $25$ 分。因为一件非常麻烦的事情：我们要处理那些辐射范围超出边界的贡献，但这里还是太麻烦了，就先用图示表示一下需要特判的情况，这里用红线代表假设没有边界差分数组值的位置，绿线表示最终差分数组值的位置。

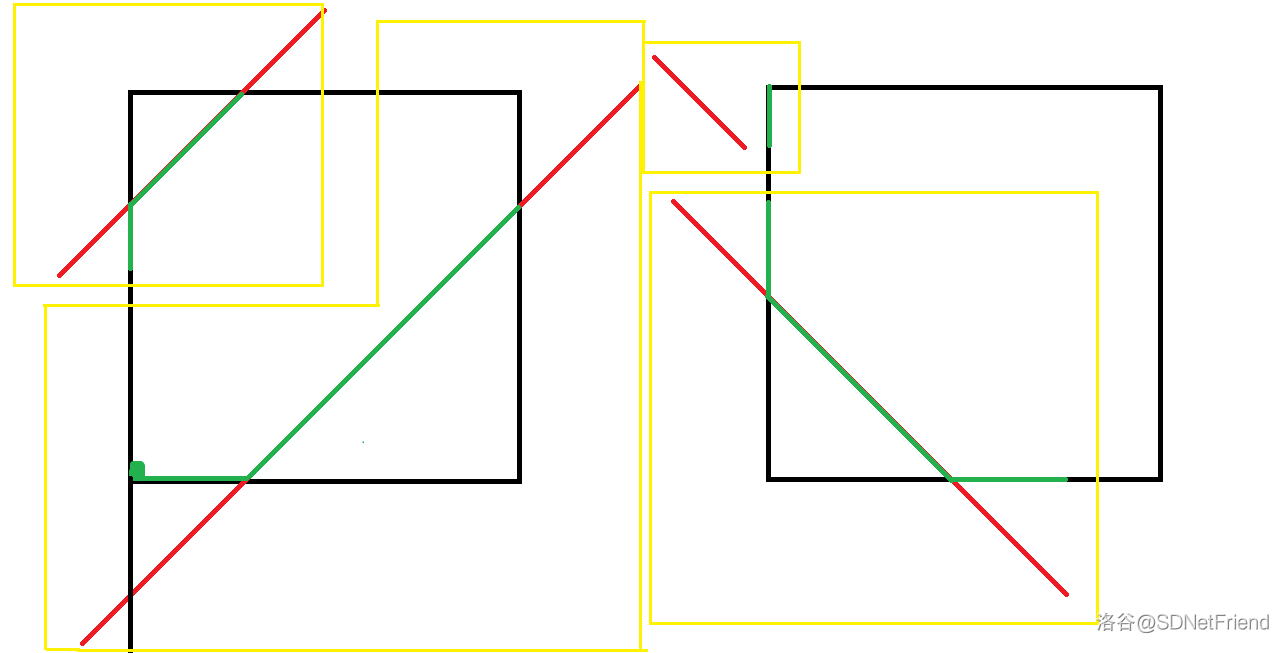
每一个黄框是一种要特判的情况。黑框就是 $W,H$ 限定出来的范围。注意左侧范围左下角有个绿团，这个意思是在范围左下角区域内所有要加的差分数组贡献都会被加到左下角这个点上，也是特判一下就好。

对于这个横着的和竖着的贡献同样是再开一个差分数组进行矩形加就可以了。

最后三个差分数组的差分数组分别做对应方向的前缀和加起来就能得到差分数组了。

如果觉得不太好想可以想象一下差分数组每个点的贡献区间都是以这个点为左下角，向右向上无限延伸的一个矩形，然后就可以判断哪些有贡献哪些没有贡献以及具体该贡献在什么位置了。

代码

#include <bits/stdc++.h>
#define lint long long
using namespace std;
inline int read(){
	char c;int f=1,res=0;
	while(c=getchar(),!isdigit(c))if(c=='-')f*=-1;
	while(isdigit(c))res=res*10+c-'0',c=getchar();
	return res*f;
}
const int W=3e6+5,N=2e5+5;
int w,h,n,q;bool flg;
vector<lint> s[W];
vector<int> d0[W],d1[W],dd[W];
inline void adds(int x,int y,lint v){
	x=max(1,x);y=max(1,y);
	if(x<=w&&y<=h)s[x][y]+=v;
}
inline void ux(int l,int r,int y,lint v){
	if(l>r)return;
	dd[l][y]+=v;
	if(r<w)dd[r+1][y]-=v;
	if(y<h)dd[l][y+1]-=v;
	if(r<w&&y<h)dd[r+1][y+1]+=v;
}
inline void uy(int l,int r,int x,lint v){
	if(l>r)return;
	dd[x][l]+=v;
	if(x<w)dd[x+1][l]-=v;
	if(r<h)dd[x][r+1]-=v;
	if(x<w&&r<h)dd[x+1][r+1]+=v;
}
inline void add0(int x,int y,lint v){
	if(x>w||y>h)return;
	if(x>=1&&y>=1)
		{d0[x][y]+=v;return;}
	int d=max(1-x,1-y),nx=x+d,ny=y+d;
	d0[nx][ny]+=v;
	if(nx==1){
		uy(max(1,y),ny-1,1,v);
		if(y<1)s[1][1]+=(1-y)*v;
	}else{
		ux(max(1,x),nx-1,1,v);
		if(x<1)s[1][1]+=(1-x)*v;
	}
}
inline void add1(int x,int y,lint v){
	if(x-w>h-y||y>h)return;
	if(1<=x&&x<=w&&1<=y&&y<=h){
		d1[x][y]+=v;
		int d=min(x-1,h-y),nx=x-d,ny=y+d;
		if(nx==1)uy(ny+1,h,1,v);
		return;
	}int d=max(x-w,1-y),nx=x-d,ny=y+d;
	if(d<0){
		if(x<1&&y<=h)
			uy(y,h,1,v);
	}else{
		d1[nx][ny]+=v;
		if(ny==1)ux(nx+1,min(w,x),1,v);
		d=min(nx-1,h-ny);
		int nx2=nx-d,ny2=ny+d;
		if(nx2==1)uy(ny2+1,h,1,v);
	}
}
inline void calc(){
	int x=read(),y=read();
	if(flg)swap(x,y);
	lint a=read(),b=read();
	int d=a/b-1;
	adds(x-d-1,y-d-1,a%b);
	adds(x+d+2,y+d+2,a%b);
	adds(x-d-1,y+d+2,-a%b);
	adds(x+d+2,y-d-1,-a%b);
	add0(x-d,y-d,b);
	add0(x+d+2,y+d+2,-b);
	add1(x+d+1,y-d,-b);
	add1(x-d-1,y+d+2,b);
}
inline void build(){
	for(int i=1;i<=w;++i)
		for(int j=1;j<=h;++j){
			d0[i][j]+=d0[i-1][j-1];
			dd[i][j]+=dd[i][j-1]+dd[i-1][j];
			dd[i][j]-=dd[i-1][j-1];
		}
	for(int i=w-1;i>=1;--i)
		for(int j=1;j<=h;++j)
			d1[i][j]+=d1[i+1][j-1];
	for(int i=1;i<=w;++i)
		for(int j=1;j<=h;++j){
			s[i][j]+=dd[i][j]+d0[i][j]+d1[i][j];
			s[i][j]+=s[i][j-1]+s[i-1][j]-s[i-1][j-1];
		}
	for(int i=1;i<=w;++i)
		for(int j=1;j<=h;++j){
			s[i][j]+=s[i][j-1]+s[i-1][j];
			s[i][j]-=s[i-1][j-1];
		}
}
inline lint query(int x0,int y0,int x1,int y1){
	--x0;--y0;
	return s[x1][y1]-s[x1][y0]-s[x0][y1]+s[x0][y0];
}
int main(){
	w=read();h=read();
	if(w>h)swap(w,h),flg=true;
	for(int i=0;i<=w;++i){
		s[i].resize(h+1);dd[i].resize(h+1);
		d0[i].resize(h+1);d1[i].resize(h+1);
	}n=read();
	for(int i=1;i<=n;++i)calc();
	build();q=read();
	while(q--){
		int x0=read(),y0=read();
		int x1=read(),y1=read();
		if(flg)swap(x0,y0),swap(x1,y1);
		lint t=(x1-x0+1)*(y1-y0+1);
		lint res=query(x0,y0,x1,y1),ans=res/t;
		if(res%t*2>=t)++ans;
		printf("%lld\n",ans);
	}return 0;
}