自动搬运

查看原文

来自洛谷，原作者为

	Anguei 俺咕诶

搬运于2025-08-24 22:03:35，当前版本为作者最后更新于2018-08-22 19:51:06，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

什么是 2-SAT？

首先，把「2」和「SAT」拆开。SAT 是 Satisfiability 的缩写，意为可满足性。即一串布尔变量，每个变量只能为真或假。要求对这些变量进行赋值，满足布尔方程。

举个例子：教练正在讲授一个算法，代码要给教室中的多位同学阅读，代码的码风要满足所有学生。假设教室当中有三位学生：Anguei、Anfangen、Zachary_260325。现在他们每人有如下要求：

• Anguei: 我要求代码当中满足下列条件之一：
  1. 不写 using namespace std; （ $\neg a$）
  2. 使用读入优化 （$b$）
  3. 大括号不换行 （$\neg c$）
• Anfangen: 我要求代码当中满足下条件之一：
  1. 写 using namespace std; （$a$）
  2. 使用读入优化 （$b$）
  3. 大括号不换行 （$\neg c$）
• Zachary_260325：我要求代码当中满足下条件之一：
  1. 不写 using namespace std; （$\neg a$）
  2. 使用 scanf （$\neg b$）
  3. 大括号换行 （$c$）

我们不妨把三种要求设为 $a,b,c$，变量前加 $\neg$ 表示「不」，即「假」。上述条件翻译成布尔方程即：$(\neg a\vee b\vee\neg c) \wedge (a\vee b\vee\neg c) \wedge (\neg a\vee\neg b\vee c)$。其中，$\vee$ 表示或，$\wedge$ 表示与。（就像集合中并集交集一样）

现在要做的是，为 ABC 三个变量赋值，满足三位学生的要求。

Q: 这可怎么赋值啊？暴力？

A: 对，这是 SAT 问题，已被证明为 NP 完全 的，只能暴力。

Q: 那么 2-SAT 是什么呢？

A: 2-SAT，即每位同学 只有两个条件（比如三位同学都对大括号是否换行不做要求，这就少了一个条件）不过，仍要使所有同学得到满足。于是，以上布尔方程当中的 $c,\neg c$ 没了，变成了这个样子：$(\neg a\vee b) \wedge (a\vee b) \wedge (\neg a\vee\neg b)$

怎么求解 2-SAT 问题？

使用强连通分量。 对于每个变量 $x$，我们建立两个点：$x, \neg x$ 分别表示变量 $x$ 取 true 和取 false。所以，图的节点个数是两倍的变量个数。在存储方式上，可以给第 $i$ 个变量标号为 $i$，其对应的反值标号为 $i + n$。对于每个同学的要求 $(a \vee b)$，转换为 $\neg a\rightarrow b\wedge\neg b\rightarrow a$。对于这个式子，可以理解为：「若 $a$ 假则 $b$ 必真，若 $b$ 假则 $a$ 必真」然后按照箭头的方向建有向边就好了。综上，我们这样对上面的方程建图：

于是我们得到了这么一张图：

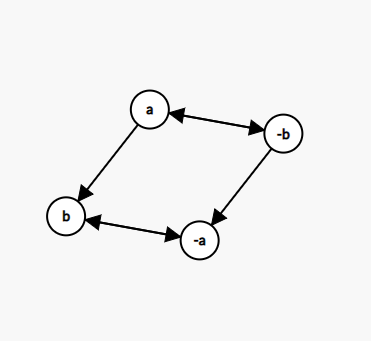
可以看到，$\neg a$ 与 $b$ 在同一强连通分量内，$a$ 与 $\neg b$ 在同一强连通分量内。同一强连通分量内的变量值一定是相等的。也就是说，如果 $x$ 与 $\neg x$ 在同一强连通分量内部，一定无解。反之，就一定有解了。

但是，对于一组布尔方程，可能会有多组解同时成立。要怎样判断给每个布尔变量赋的值是否恰好构成一组解呢？

这个很简单，只需要 当 $x$ 所在的强连通分量的拓扑序在 $\neg x$ 所在的强连通分量的拓扑序之后取 $x$ 为真 就可以了。在使用 Tarjan 算法缩点找强连通分量的过程中，已经为每组强连通分量标记好顺序了——不过是反着的拓扑序。所以一定要写成 color[x] < color[-x] 。

时间复杂度：$O(N + M)$

说了这么多，咋不上代码啊？

核心代码在下面。

建图

n = read(), m = read();
for (int i = 0; i < m; ++i) {
    // 笔者习惯对 x 点标号为 x，-x 标号为 x+n，当然也可以反过来。
    int a = read(), va = read(), b = read(), vb = read();
    if (va && vb) { // a, b 都真，-a -> b, -b -> a
        g[a + n].push_back(b);
        g[b + n].push_back(a);
    } else if (!va && vb) { // a 假 b 真，a -> b, -b -> -a
        g[a].push_back(b);
        g[b + n].push_back(a + n);
    } else if (va && !vb) { // a 真 b 假，-a -> -b, b -> a
        g[a + n].push_back(b + n);
        g[b].push_back(a);
    } else if (!va && !vb) { // a, b 都假，a -> -b, b -> -a
        g[a].push_back(b + n);
        g[b].push_back(a + n);
    }
}

当然，还有更精简的位运算建图方式，可以免去上面的四个 if：

n = read(), m = read();
for (int i = 0; i < m; ++i) {
    int a = read(), va = read(), b = read(), vb = read();
    g[a + n * (va & 1)].push_back(b + n * (vb ^ 1));
    g[b + n * (vb & 1)].push_back(a + n * (va ^ 1));
}

找环

// 注意所有东西都要开两倍空间，因为每个变量存了两次
void tarjan(int u) {
    low[u] = dfn[u] = ++dfsClock;
    stk.push(u); ins[u] = true;
    for (const auto &v : g[u]) {
        if (!dfn[v]) tarjan(v), low[u] = std::min(low[u], low[v]);
        else if (ins[v]) low[u] = std::min(low[u], dfn[v]);
    }
    if (low[u] == dfn[u]) {
        ++sccCnt;
        do {
            color[u] = sccCnt;
            u = stk.top(); stk.pop(); ins[u] = false;
        } while (low[u] != dfn[u]);
    }
}
// 笔者使用了 Tarjan 找环，得到的 color[x] 是 x 所在的 scc 的拓扑逆序。
for (int i = 1; i <= (n << 1); ++i) if (!dfn[i]) tarjan(i);

输出

for (int i = 1; i <= n; ++i)
    if (color[i] == color[i + n]) { // x 与 -x 在同一强连通分量内，一定无解
        puts("IMPOSSIBLE");
        exit(0);
    }
puts("POSSIBLE");
for (int i = 1; i <= n; ++i)
    print((color[i] < color[i + n])), putchar(' '); // 如果不使用 Tarjan 找环，请改成大于号
puts("");