自动搬运

查看原文

来自洛谷，原作者为

	command_block 众水皆昂首，饮月唯我一。

搬运于2025-08-24 22:03:30，当前版本为作者最后更新于2021-06-16 13:38:41，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

本大胖题的阳间做法，不用分类讨论了！

题意 ：给出一棵 $n$ 个点的树，边有正边权。

给出树上的 $m$ 条路径，每条路径有一个花费。

选出两条路径，使得两条路径至少有一条公共边，且两条路径的并的边权和减去花费和最大。或指出不存在满足要求的方案。

多组数据，$n\leq 5\times 10^4,m\leq 10^5,\sum n\leq 10^6,\sum m\leq 2\times 10^6$。时限$\texttt{8s}$。

---

对于给出的花费为 $w$ 的路径 $(u,v)$ ，我们记 $c_{(u,v)}=dis(u,v)-2w$。

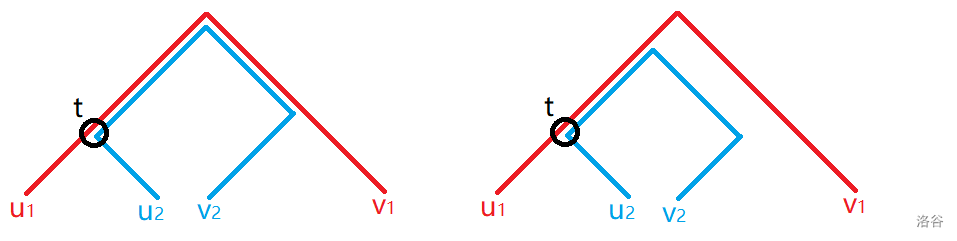
可能的两种合法方案如图。对于两种情况，收益的两倍均为 ：

$$c_{(u_1,v_1)}+c_{(u_2,v_2)}+dis(u_1,u_2)+dis(v_1,v_2) $$

考虑枚举 $t={\rm lca}(u_1,u_2)$ （即相交部分最深的点）

然后求出最大的

$$c_{(u_1,v_1)}+c_{(u_2,v_2)}+dep_{u_1}+dep_{u_2}+dis(v_1,v_2) $$

还要加上此时确定的 $-2dep_{{\rm lca}(u_1,u_2)}$。

这可以看做将 $v_1$ 的权值定为 $w_{v_1}=c_{(u_1,v_1)}+dep_{u_1}$ ，而 $v_2$ 的权值定为 $w_{v_2}=c_{(u_2,v_2)}+dep_{u_2}$。

选择 $v_1,v_2$ 两者配对的贡献为 $w_{v_1}+w_{v_2}+dis(v_1,v_2)$。

这是经典的树上（带权）最远点对问题，有结论 ：

• 记 ${\rm diam}(S)$ 为树上点集 $S$ 的最远点对。

  对于 $S=S_1∪S_2$ ，有 ${\rm diam}(S)={\rm diam}\big({\rm diam}(S_1)∪{\rm diam}(S_2)\big)$

  可见 P2056 [ZJOI2007]捉迷藏。

利用这个结论，只需计算 $O(1)$ 次两点距离，就能合并点集最远点对，或者计算两个点集之间的最远点对。

使用 $O(1)\ \rm LCA$ ，这个复杂度就是 $O(1)$。

记 $S_u$ 为子树内的路径提供的匹配候选点集。

对于 $t$ ，要计算 $t$ 的各个子分支之间的贡献。

对于路径 $(u,v)$ ，记 $t={\rm lca}(u,v)$。则 $u$ 会出现在 $S_{[v\rightarrow t)}$ 中， $v$ 会出现在 $S_{[u\rightarrow t)}$ 中。

它们不能出现在 $t$ 的祖先的 $S$ 中，否则会产生错误的匹配。

使用树上差分，我们在 $u$ 点加入，在 $u$ 到 $t$ 的路径上的倒数第二个点删除。

用线段树合并维护，在合并时即可获得不同子分支之间的贡献。

复杂度 $O\big((n+m)\log n\big)$。

不到 $\rm 4Kb$ 的代码 ：

#include<algorithm>
#include<cstring>
#include<cstdio>
#include<vector>
#define pb push_back
#define ll long long
#define MaxN 50050
#define MaxM 100500
using namespace std;
const ll INF=1ll<<60;
vector<int> g[MaxN],l[MaxN];
int dep[MaxN],f[16][MaxN]
   ,dfn[MaxN],out[MaxN],id[MaxN<<1],tim;
ll dist[MaxN];
void pfs(int u)
{
  id[dfn[u]=++tim]=u;
  for (int i=0,v;i<g[u].size();i++)
    if (!dfn[v=g[u][i]]){
      dep[v]=dep[f[0][v]=u]+1;
      dist[v]=dist[u]+l[u][i];
      pfs(v);id[++tim]=u;
    }
  out[u]=tim;
}
#define Pii pair<int,int>
#define Pr pair<int,ll>
#define fir first
#define sec second
#define mp make_pair
int lg2[MaxN<<1];
Pii t[18][MaxN<<1];
void Init()
{
  for (int i=2;i<=tim;i++)lg2[i]=lg2[i>>1]+1;
  for (int i=1;i<=tim;i++)t[0][i]=mp(dep[id[i]],id[i]);
  for (int j=1;(1<<j)<=tim;j++)
    for (int i=1;i+(1<<j)-1<=tim;i++)
      t[j][i]=min(t[j-1][i],t[j-1][i+(1<<(j-1))]);
}
int lca(int u,int v){
  u=dfn[u];v=dfn[v];if (u>v)swap(u,v);
  int k=lg2[v-u+1];
  return min(t[k][u],t[k][v-(1<<k)+1]).second;
}
int up(int u,int t){
  int k=15;
  while(k--)while(dep[f[k][u]]>dep[t])u=f[k][u];
  return u;
}
ll dis(int u,int v)
{return dist[u]+dist[v]-2*dist[lca(u,v)];}
inline ll dis(Pr u,Pr v)
{return dis(u.fir,v.fir)+u.sec+v.sec;}
struct Data{Pr u,v;}Z;
ll merge(Data &S,const Data &A,const Data &B)
{
  if (!A.u.fir&&!A.v.fir){S=B;return -INF;}
  if (!B.u.fir&&!B.v.fir){S=A;return -INF;}
  ll ret,mx=-INF,s;int op=-1;
  #define chk(u,v,w) if (u.fir&&v.fir){s=dis(u,v);if (s>mx){mx=s;op=w;}}
  chk(A.u,B.u,3);chk(A.u,B.v,4);
  chk(A.v,B.u,5);chk(A.v,B.v,6);
  ret=mx;
  chk(A.u,A.v,1);chk(B.u,B.v,2);
  if (op==1)S=A;if (op==2)S=B;
  if (op==3)S=(Data){A.u,B.u};if (op==4)S=(Data){A.u,B.v};
  if (op==5)S=(Data){A.v,B.u};if (op==6)S=(Data){A.v,B.v};
  return ret;
}
struct Node{int l,r;Data x;}a[MaxM*40];
int rt[MaxN],tn,to;Pr wfc;
void up(int u){
  if (!a[u].l||!a[u].r){a[u].x=a[a[u].l|a[u].r].x;return ;}
  merge(a[u].x,a[a[u].l].x,a[a[u].r].x);
}
void add(int l,int r,int &u)
{
  if (!u)u=++tn;
  if (l==r){a[u].x.u=wfc;return ;}
  int mid=(l+r)>>1;
  if (to<=mid)add(l,mid,a[u].l);
  else add(mid+1,r,a[u].r);
  up(u);
}
void del(int l,int r,int &u)
{
  if (l==r){a[u].x.u=mp(0,0);return ;}
  int mid=(l+r)>>1;
  if (to<=mid)del(l,mid,a[u].l);
  else del(mid+1,r,a[u].r);
  up(u);
}
int merge(int u,int v)
{
  if (!u||!v)return u|v;
  merge(a[u].x,a[u].x,a[v].x);
  a[u].l=merge(a[u].l,a[v].l);
  a[u].r=merge(a[u].r,a[v].r);
  return u;
}
ll ans;
vector<int> b[MaxN];
int n,m;
void dfs(int u)
{
  for (int i=0,v;i<g[u].size();i++)
    if (dep[v=g[u][i]]>dep[u]){
      dfs(v);
      ans=max(ans,merge(Z,a[rt[u]].x,a[rt[v]].x)-2*dist[u]);
      rt[u]=merge(rt[u],rt[v]);
    }
  for (int i=0;i<b[u].size();i++)
    {to=b[u][i];del(1,m,rt[u]);}
}
void solve()
{
  scanf("%d",&n);
  for (int i=1,u,v,w;i<n;i++){
    scanf("%d%d%d",&u,&v,&w);
    g[u].pb(v);l[u].pb(w);
    g[v].pb(u);l[v].pb(w);
  }dep[1]=1;pfs(1);Init();
  for (int j=1;j<15;j++)
    for (int i=1;i<=n;i++)
      f[j][i]=f[j-1][f[j-1][i]];
  scanf("%d",&m);
  ans=-INF;
  for (int i=1;i<=m;i++){
    int u,v;ll w;
    scanf("%d%d%lld",&u,&v,&w);
    if (u==v)continue;
    w=dis(u,v)-2*w;
    int t=lca(u,v),tu=up(u,t),tv=up(v,t);
    to=i;
    if (u!=t){
      wfc=mp(v,w+dist[u]);
      ans=max(ans,merge(Z,(Data){wfc,mp(0,0)},a[rt[u]].x)-2*dist[u]);
      add(1,m,rt[u]);b[tu].pb(i);
    }
    if (v!=t){
      wfc=mp(u,w+dist[v]);
      ans=max(ans,merge(Z,(Data){wfc,mp(0,0)},a[rt[v]].x)-2*dist[v]);
      add(1,m,rt[v]);b[tv].pb(i);
    }
  }
  dfs(1);
  if (ans<=-INF/10)puts("F");
  else printf("%lld\n",ans/2);
  for (int i=1;i<=n;i++){
    g[i].clear();l[i].clear();b[i].clear();
    dfn[i]=rt[i]=0;
  }memset(a,0,sizeof(Node)*(tn+5));tn=tim=0;
}
int main()
{
  int T;scanf("%d",&T);
  while(T--)solve();
  return 0;
}

所以，2018 年最难题还应该是 D2T3 (