自动搬运

查看原文

来自洛谷，原作者为

	ez_lcw **

搬运于2025-08-24 22:03:18，当前版本为作者最后更新于2019-09-15 07:27:11，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

考虑树形$dp$，设$dp[i]$表示以$i$为根的子树中路线的最大数量（即这棵子树的最优解），$un[i][]$表示以$i$为根的子树中，所有的点$u$，当且仅当$i$到$u$的路径上不与$i$子树的最优解中的某条路径相交。

那么考虑用子树合并根。

对于$dp[u]$，我们先加上每个儿子的$dp$值，然后我们再考虑下面这两种情况：

1. 对于$u$的某一个儿子$son$，如果$son$的子树内（包括$son$自己）有一个点$v=un[son][i]$与$u$之间有路径$(u,v)$，如图：

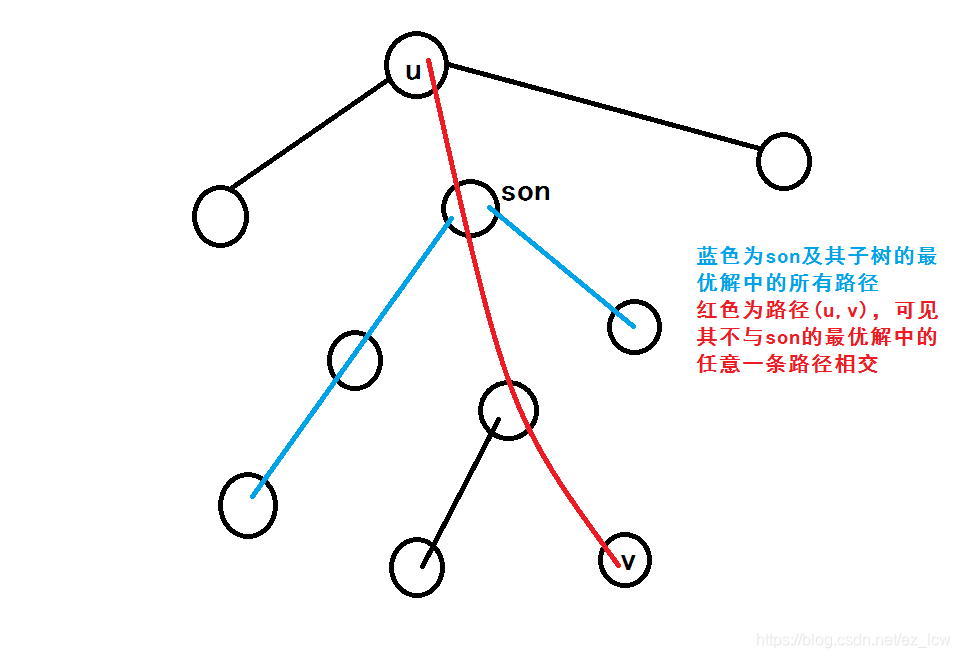   可能对于某一个儿子$son$，这种路径可能有很多条，但是选任意一条都可以，因为边$(u,v)$只能走一遍。

2. 对于$u$的某两个不同的儿子$son_1$、$son_2$，它们各自子树内（包括$son_1$、$son_2$）分别有两个点$a=un[son_1][i]$、$b=un[son_2][j]$，且有一条路径$(a,b)$，我们就把$link[son_1][son_2]$设为$1$，如图：

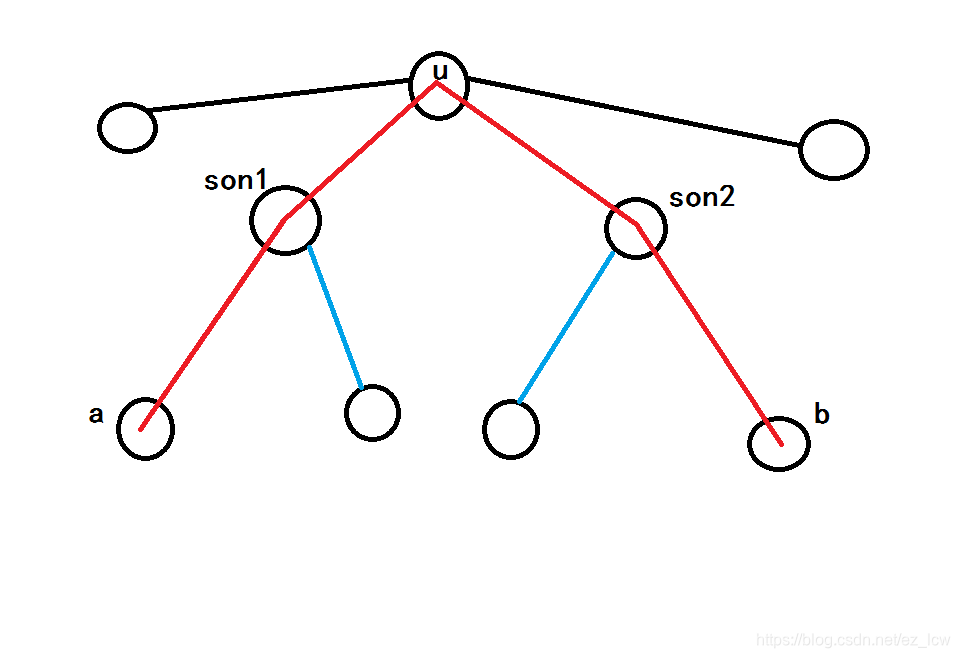   那么对于某个儿子$son_1$，它可能可以匹配到很多个$son_2$，所以怎么选择才方案最优是解决问题的关键，所以我们考虑状压$dp$。

   设$f[i]$表示状态$i$的最优解，状态$i$的二进制表达式的第$x$位若为$1$，则表示已经考虑过加入这个儿子的情况了。

   那么我们从小到大枚举$i$，找到$a=\_\_builtin\_ctz(i)$，$lb=lowbit(i)$，则$i$可以从$i-lb$转移过来，因为在$i-lb$的二进制表达式中，第$a$位为$0$；在$i$的二进制表达式中，第$a$位为$1$。

   所以现在我们考虑的是考虑过加入儿子$a$，也就是上文的$son_1$，那么我们还要枚举$son_2$，即下文的$b$。

   对于每一个$b$，当$link(a,b)=1$且$i$的二进制表达式中第$b$位为$1$时，我们取：

   $$f[i]=max(f[i],f[i-(1<<a)-(1<<b)]+1)$$

   即从$i$的第$a$位为$0$且第$b$位为$0$时转移过来。

   最后$dp[u]+=f[2^{u\text{的儿子个数}}-1]$即可。

这样就合并完成了。

记得合并完后维护一下$un[u]$。

最后输出$dp[1]$就好了。

完整代码加注释如下：

#include<bits/stdc++.h>
 
#define N 1010
#define D 15
 
using namespace std;
 
int T,n,m;
int dp[N],f[1<<D];
int cnt,head[N],nxt[N<<1],to[N<<1];
bool vis[N][N],link[D][D];
 
vector<int>un[N];
 
int lowbit(int x)
{
    return x&-x;
}
 
void init()
{
    cnt=0;
    memset(head,0,sizeof(head));
    memset(vis,false,sizeof(vis));
    memset(dp,0,sizeof(dp));
}
 
void adde(int u,int v)
{
    to[++cnt]=v;
    nxt[cnt]=head[u];
    head[u]=cnt;
}
 
void dfs(int u,int fa)
{
    int son[D],tot=0;
    for(int i=head[u];i;i=nxt[i])
    {
        if(to[i]!=fa)
        {
            dfs(to[i],u);
            dp[u]+=dp[to[i]];
            son[tot++]=to[i];   //存储每一个儿子
        }
    }
    for(int i=0;i<tot;i++)
    {
        for(int j=0;j<un[son[i]].size();j++)
        {
            if(vis[un[son[i]][j]][u])   
            {
                dp[u]++;
                un[son[i]].clear();//由于已经选了一条边了，所以为了下面的维护un[u]，我们把un[son[i]]清零
            }       
        }
    }
    memset(link,false,sizeof(link));
    for(int i=0;i<tot;i++)
    {
        for(int j=i+1;j<tot;j++)
        {
            int a=son[i],b=son[j];
            for(int p=0;p<un[a].size();p++)
            {
                for(int q=0;q<un[b].size();q++)
                {
                    if(vis[un[a][p]][un[b][q]])
                    {
                        link[i][j]=link[j][i]=true;//标记son[i]与son[j]各自子树之间有路径
                        break;
                    }
                }
                if(link[i][j])
                    break;
            }
        }   
    }
    f[0]=0;
    int maxn=(1<<tot)-1;
    for(int i=1;i<=maxn;i++)
    {
        f[i]=f[i-lowbit(i)];
        int a=__builtin_ctz(i);
        for(int b=a+1;b<tot;b++)//枚举son2
            if(link[a][b]&&((i>>b)&1))
                f[i]=max(f[i],f[i-(1<<a)-(1<<b)]+1);
    }
    dp[u]+=f[maxn];
    un[u].push_back(u);
    for(int i=0;i<tot;i++)
        if(f[maxn]==f[maxn-(1<<i)])
            for(int j=0;j<un[son[i]].size();j++)
                un[u].push_back(un[son[i]][j]);//维护un[u]
}
 
int main()
{
    scanf("%d",&T);
    while(T--)
    {
        init();
        scanf("%d",&n);
        for(int i=1;i<=n;i++)
            un[i].clear();
        for(int i=1;i<n;i++)
        {
            int u,v;
            scanf("%d%d",&u,&v);
            adde(u,v),adde(v,u);
        }
        scanf("%d",&m);
        for(int i=1;i<=m;i++)
        {
            int u,v;
            scanf("%d%d",&u,&v);
            vis[u][v]=vis[v][u]=true;
        }
        dfs(1,0);
        printf("%d\n",dp[1]);
    }
}