自动搬运

查看原文

来自洛谷，原作者为

	Hope2075 时间的流沙，淹没梦境里的夏

搬运于2025-08-24 22:03:14，当前版本为作者最后更新于2019-03-10 21:39:58，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

稍微一想，应该就能知道题目实际没有精度问题，因为最小单位是0.25

这题看起来像区间操作

但是，题目并没有给出坐标范围

而且我也不会二维线段树

不过，如果计算一下坐标范围的话，会发现绝对值最大就是4000

$O(n^2)$的暴力应该能过

当然不能把覆盖的区域暴力设置然后统计，这样会T

考虑前缀和

在做这道题的时候建议在纸上画坐标系

输入时把l直接除以2就可以

首先，考虑第一种照片的覆盖范围

正好是一块矩形区域

直接对四个角加减一下就可以了

第二种照片就有些麻烦

考虑旋转坐标系

这一步一定要小心，不然很容易出错

可以给出任意两个坐标轴上的点，变换后看位置

我是按以下规则变换的：

$(x_0,y_0)->(x,y)$

$x=x_0+y_0$

$y=x_0-y_0$

效果就是将坐标系逆时针旋转45度，最后x轴在第四象限，y轴在第一象限

然后，这块区域就好处理了

处理完后，求一遍前缀和

接下来维护每个格子的贡献

对于第一种，会使覆盖到的所有格子贡献变为1

对于第二种，可能会比较棘手

首先我们规定两个坐标系每个格子的坐标都是左下角的坐标（就是坐标值最小的一个顶点）

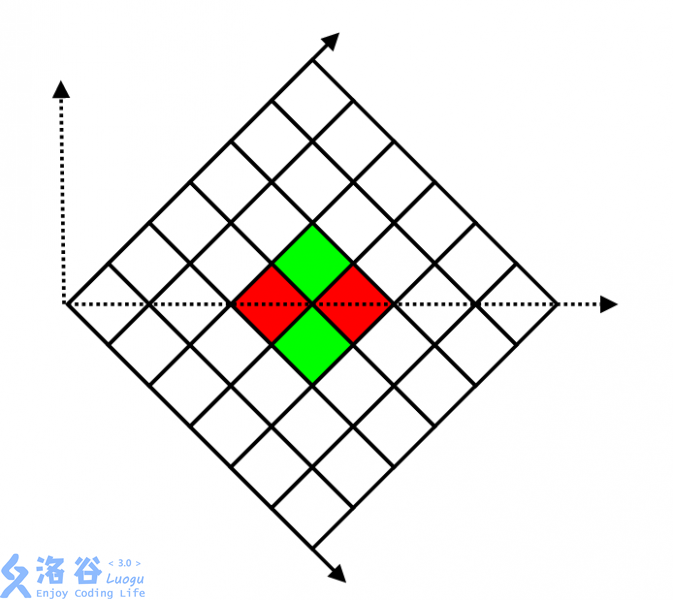
四个格子在新坐标系中的坐标分别为$(2,2),(2,3),(3,2),(3,3)$

可以推出转换回去的公式：

$x_0= \frac{x+y}{2}$

$y_0= \frac{x-y}{2}$

先考虑两坐标值之和为偶数的点，转换回去后的坐标是整数（红色格子）

可以得到左顶点坐标分别为$(2,0),(3,0)$

这时发现，贡献没法计算

考虑每个点记录四边所在三角形是否被覆盖

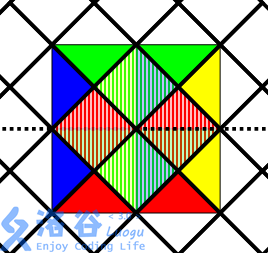
大概就是这样

（效果不太好)

对于坐标值为偶数的点，就给左端点所处格子的下部标记为已覆盖，所处格子下面格子的上部标记已覆盖

然后考虑和为奇数（原图绿色格子）

这时发现左端点转换后坐标是分数

但是上端点和下端点转化后都是整数

在转化前，把横坐标加一，就可以得到下端点坐标

这时候，给下端点所处格子的左部标记为已覆盖，所处格子左面格子的右部标记已覆盖

最后暴力扫一遍，统计总覆盖量就可以了

但是别忘了数据范围

坐标可以为负数

而且转化后坐标大致要加倍

所以注意数组大小

在对数组执行操作时要对点加上一个数，数组下标变成点的坐标要减去一个数

不要都开int，记录是否覆盖用bool就可以

这样数组大概384MB，能通过本题

另外注意常数优化，重点是求前缀和、处理覆盖和最后统计时

代码：

不一定能过，但氧化一下就差不多了

#include<iostream>
using namespace std;
const int N=4096;
int m1[N][N],m2[N*2][N*2];
bool hasl[N][N],hasr[N][N],hasu[N][N],hasd[N][N];
struct pos{
    int x,y;
    void conv(){
        x=x+y;
        y=x-y*2;
    }
    void aconv(){
        x=(x+y)/2;
        y=x-y;
    }
};
char t;
int n;
int l;
pos cur;
int cnt;
int main(){
    ios::sync_with_stdio(false);
    cin>>n;
    while(n--){
        cin>>t>>cur.x>>cur.y>>l;
        l/=2;
        if(t=='A'){
            m1[cur.x-l+2048][cur.y-l+2048]++;
            m1[cur.x+l+2048][cur.y-l+2048]--;
            m1[cur.x-l+2048][cur.y+l+2048]--;
            m1[cur.x+l+2048][cur.y+l+2048]++;
        }else{
            cur.conv();
            m2[cur.x-l+4096][cur.y-l+4096]++;
            m2[cur.x+l+4096][cur.y-l+4096]--;
            m2[cur.x-l+4096][cur.y+l+4096]--;
            m2[cur.x+l+4096][cur.y+l+4096]++;
        }
    }
    for(int i=1;i<N;i++){
        m1[i][0]+=m1[i-1][0];
    }
    for(int j=1;j<N;j++){
        m1[j][0]+=m1[0][j-1];
    }
    for(int i=1;i<N;i++){
        for(int j=1;j<N;j++){
            m1[i][j]+=m1[i-1][j]+m1[i][j-1]-m1[i-1][j-1];
        }
    }
    
    for(int i=1;i<N*2;i++){
        m2[i][0]+=m2[i-1][0];
    }
    for(int j=1;j<N*2;j++){
        m2[j][0]+=m2[0][j-1];
    }
    for(int i=1;i<N*2;i++){
        for(int j=1;j<N*2;j++){
            m2[i][j]+=m2[i-1][j]+m2[i][j-1]-m2[i-1][j-1];
        }
    }
    for(int i=0;i<N;i++){
        for(int j=0;j<N;j++){
            if(m1[i][j])
                hasl[i][j]=hasr[i][j]=hasu[i][j]=hasd[i][j]=1;
        }
    }
    for(int i=0;i<N*2;i++){
        for(int j=0;j<N*2;j++){
            if(m2[i][j]){
                if((i^j)&1){
                    hasl[(i+1+j)/2-4096+2048][(i-1-j)/2+2048]=1;
                    hasr[(i+1+j)/2-4096-1+2048][(i-1-j)/2+2048]=1;
                }else{
                    hasu[(i+j)/2-4096+2048][(i-j)/2+2048]=1;
                    hasd[(i+j)/2-4096+2048][(i-j)/2-1+2048]=1;
                }
            }
        }
    }
    for(int i=0;i<N;i++){
        for(int j=0;j<N;j++){
            cnt+=hasl[i][j]+hasr[i][j]+hasu[i][j]+hasd[i][j];
        }
    }
    cout<<(cnt/4)<<".";
    cnt%=4;
    switch(cnt){
        case 0:
            cout<<"00";
            break;
        case 1:
            cout<<"25";
            break;
        case 2:
            cout<<"50";
            break;
        case 3:
            cout<<"75";
            break;
    }
}