自动搬运

查看原文

来自洛谷，原作者为

	WinXP **

搬运于2025-08-24 22:03:11，当前版本为作者最后更新于2018-07-11 08:29:14，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

我又来写毒瘤题解啦

我们一看这题，哇，我会网络流！

网络流:什么鬼？管我什么事？

考虑建出这样一个图。

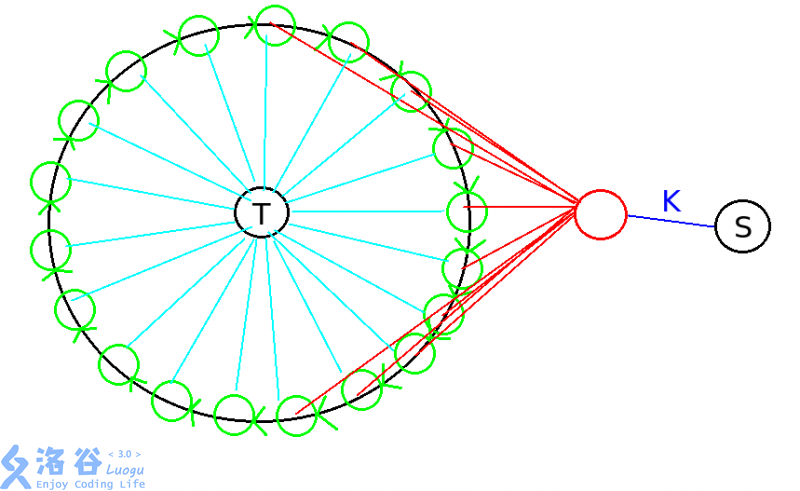
毒瘤思路毒瘤图

具体来说就是由 $S$ 向一个点连费用为 $0$ 流量为 $k$ 的边。再由这个点向所有点连一条费用为 $0$ 流量为 $1$ 的边。由所有的点向他的下一个点连边，流量为 $1$ ，费用为 $a_i$ 。再由所有的点向 $T$ 连边，流量为 $1$ 费用为 $0$，跑最大费用最大流。

这样相当于我们完全模拟出了选 $k$ 次的过程，而决策交给算法。别急着写，这个范围显然不是网络流的范围(我也不知道能不能大力跑过)，能不能考虑手动模拟网络流的决策?

如果当 $k$ 为 $1$ 的时候，我们可以知道这个做法就是在求出最长链。取完这条链出来之后，考虑将这条链上的所有点取反。在下一次的过程中，如果选出的第二条链与第一条链没有交集，这个显然是对的；如果选出的第二条链与第一条链包含或者被包含，相当于我们贪心反悔，把更大的链分割成两条链来选；不过如果选出的链与第一条链有交集而且不包含，就会出问题，因为网络流中退流的过程保证这种选法是不合法的。

而这种选法不会出现。

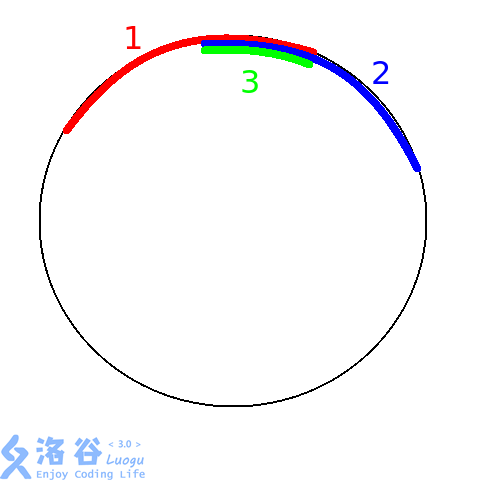
对于这种情况，我们设这三条链的编号为 $1,2,3$ ，具体如上图。设 $2$ 号链如果是后选出来的链，根据决策我们知道 $2$ 号链是最长链；既然 $2$ 号链是最长链则 $3$ 号链现在的值显然大于 $0$ ，否则不能选；因为 $3$ 号链现在的值大于 $0$，说明在选 $1$ 号链的时候， $3$ 号链的值小于 $0$ ，才能被取反成大于 $0$ 的链；但是选 $1$ 号链也是最长链，不可能把值为负的 $3$ 号链包含在内。所以这种情况是不合法的。

然后就可以开心敲代码了---吗?

有一个小问题。如果 $k$ 比正数的个数少，我们知道必须要多选出一些最小的负数出来才能满足题意。而网络流的做法是默认每次选中的链大于 $0$ ，因为如果小于 $0$ 直接就流进 $T$ 了。对于这种情况需要特判。

顺便说一下如何求最长链：链长度翻一倍模拟环拆链，对于每个点维护前缀和，对于每一个点 $i$ 计 $P_i$ 为它的前缀和，即为求 $P_i-min(P_j)\quad (j<i)$，维护这个过程可以用单调队列实现。
不过话说dp好像也要用单调队列优化一下。

然后就可以开心敲代码啦~

#include <bits/stdc++.h>
#define rap(i,s,n) for(int i=s;i<=n;i++)
#define drap(i,n,s) for(int i=n;i>=s;i--)
#define N 210000
#define inf 0x3f3f3f3f
#define ll long long
#define m(s,k) memset(s,k,sizeof s)
using namespace std;
char xB[1<<15],*xS=xB,*xTT=xB;
#define getc() (xS==xTT&&(xTT=(xS=xB)+fread(xB,1,1<<15,stdin),xS==xTT)?0:*xS++)
#define isd(c) ((c>='0'&&c<='9')||(c=='-'))
template<typename T>
inline bool rd(T& xa){
    char xchh; T f=1; while(xchh=getc(),(!isd(xchh))&&(xchh!=0));
    if(xchh==0) return 0; if(xchh=='-') xchh=getc(),f=-1; xa=xchh-'0';
    while(xchh=getc(),isd(xchh)) xa=xa*10+xchh-'0'; xa*=f; return 1;
}
int n,k,a[N],pre[N],ans;
struct mqueue{
	//单调队列
    int g[N],t[N],r,l;
    void init(){r=0,l=1;}
    void in(int x,int xt){while(r>=l&&g[r]>=x) r--; g[++r]=x,t[r]=xt;}
    int tmin(){return t[l];} int gmin(){return g[l];}
    void push(int xt){while(l<=r&&t[l]<=xt) l++;}
}q;
int main(){
    rd(n); rd(k); rap(i,1,n) rd(a[i]); 
    int dk=0; rap(i,1,n) if(a[i]>0) dk++; if(dk<=k){
        sort(a+1,a+n+1); drap(i,n,1){
            if(k==0) break; ans+=a[i]; k--;
        }
        printf("%d\n",ans); return 0;
        //特判
    }
    while(k--){
        q.init(); int maxv=-inf,maxt=0,fx;
        rap(i,1,n) a[i+n]=a[i],pre[i]=a[i]+pre[i-1],q.in(pre[i],i);
        rap(i,n+1,2*n){
            pre[i]=a[i]+pre[i-1];
            if(maxv<pre[i]-q.gmin()) maxv=pre[i]-q.gmin(),maxt=i,fx=q.tmin();
            q.in(pre[i],i); q.push(i-n);
        }
        //求出最长链 我为了方便写求的是左开右闭..
        if(maxt==0) return 0; ans+=maxv;
        rap(i,fx,maxt-1) a[i%n+1]=-a[i%n+1];
    }
    printf("%d\n",ans);
    return 0;
}