1 条题解
-
0
自动搬运
来自洛谷,原作者为

约瑟夫用脑玩
AFO搬运于
2025-08-24 22:03:08,当前版本为作者最后更新于2021-01-09 17:37:56,作者可能在搬运后再次修改,您可在原文处查看最新版自动搬运只会搬运当前题目点赞数最高的题解,您可前往洛谷题解查看更多
以下是正文
题意:
输入一棵树,求把这棵树放入 的网格图中的方案数,对 取模。
要求: 在左上角,有边连接的节点必须相邻。
题解:
有点小妙的 (其实就是我没想到)。
其实情况不算太多(吧)。
先把 当做根。
设 表示以 为左上角,它本身以及子树全部放进去了的方案数。
可以看做 左边暂时为墙,不能放,答案即为 。
首先注意到每个点最多只有两个儿子,即度数不超过三。
考虑转移,设当前节点为 :
-
若 没有儿子: 。
即:
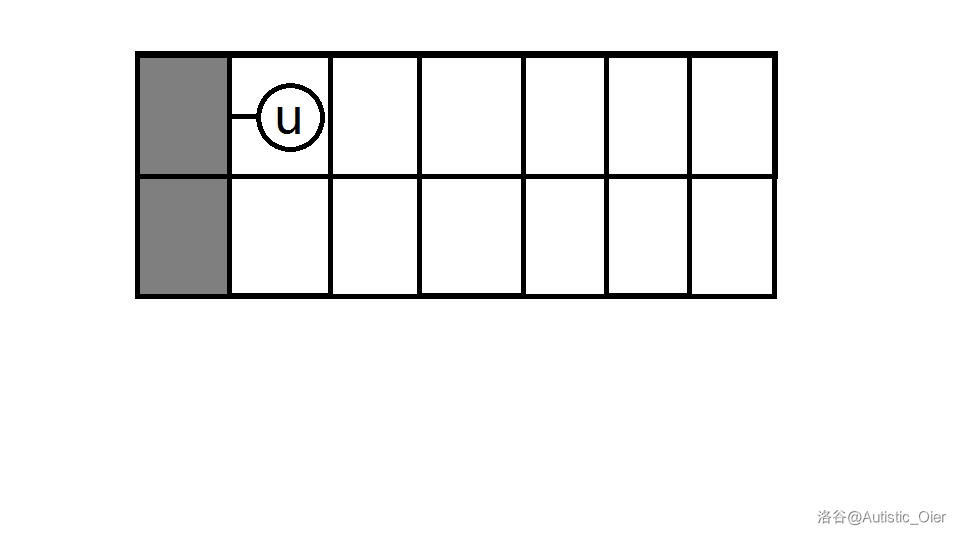
-
若 只有一个儿子:
-
先考虑将其儿子,设为 ,放在其下面。
-
若 没有儿子, 。
-
若 只有一个儿子 , 。
即:
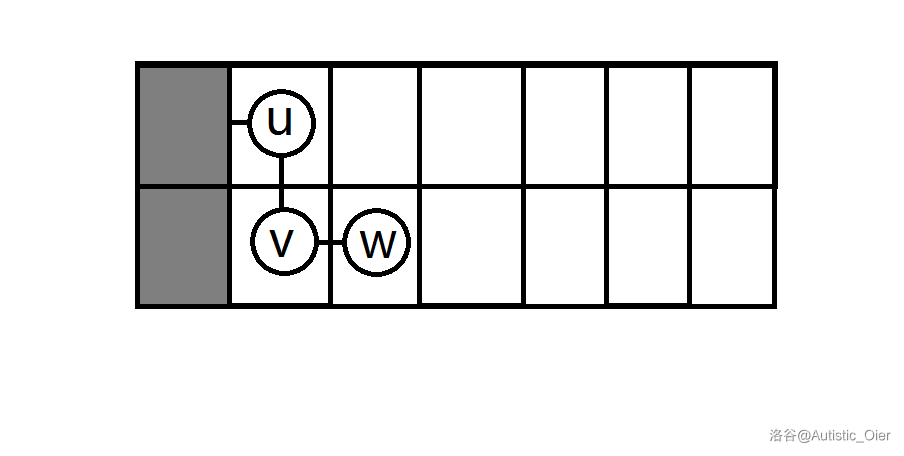
-
若 有两个儿子,不能贡献方案。
-
-
再考虑将其儿子放在其右边,考虑 下方是否放点。
-
若不放,设其儿子为 ,则显然有 。
即:
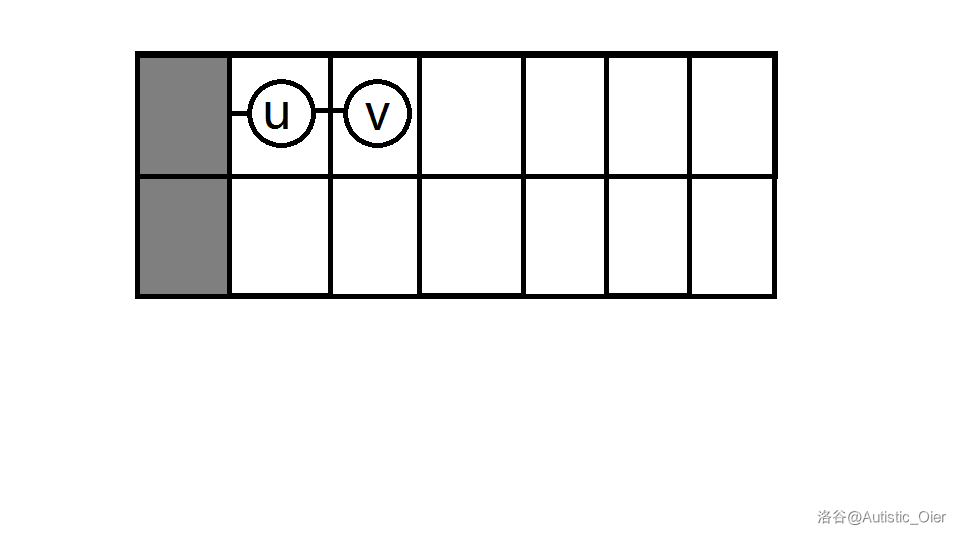
-
若放,考虑如下情况:
-
若 及其子树为一条长度大于 的偶链,则 。
即:
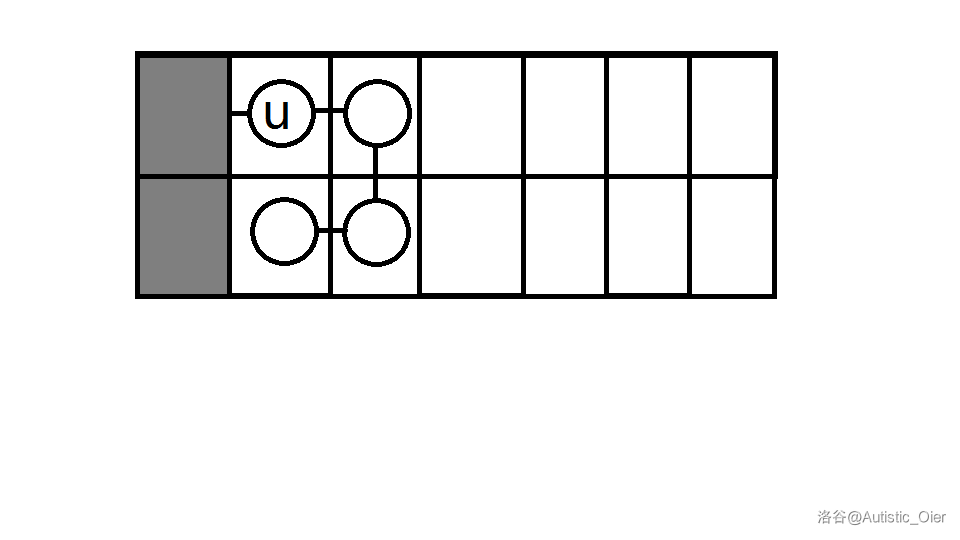
否则,设 第一个有两个儿子的节点为 ,叫做 的分叉节点。
-
若 (设为 )的一个儿子为链。
由于必须在 下放点,则需满足将链折过去后恰好在 底下,有两种情况: 或 ,设 的另一个儿子为 ,此时 。
即:
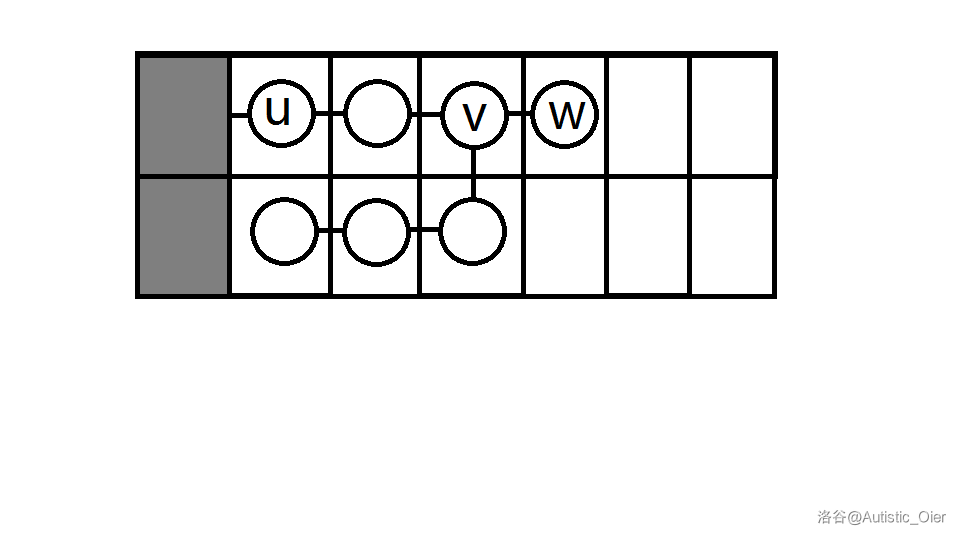
或
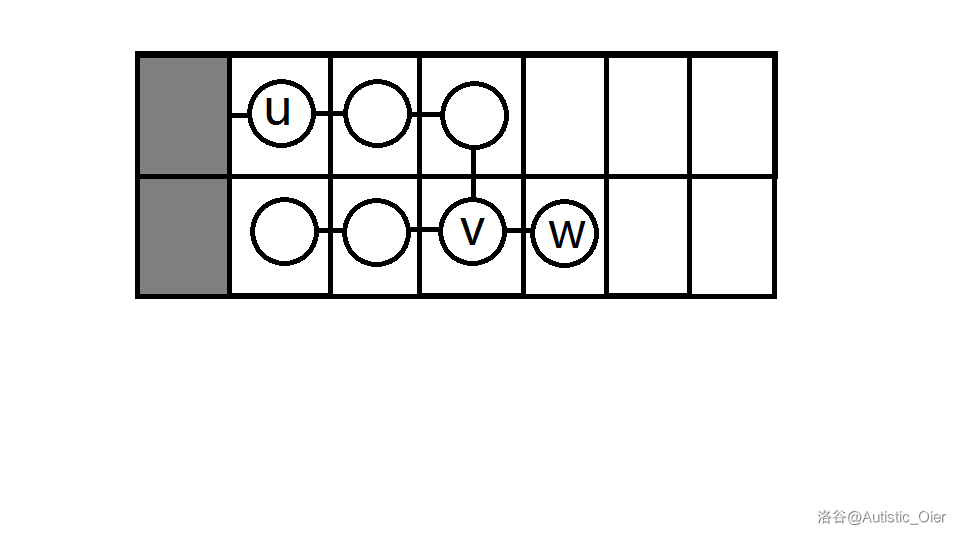
注:将左下与左上翻折后是一样的,故方案数相同,均为 。
否则设 (设为 )的一个儿子为 ,同理,要满足折一条链到 的底下,需 的一个儿子为链且满足: 。
此时设 的另一个儿子为 , 的另一个儿子为 。
-
若 与 恰为长度相同的链,则 。
即:
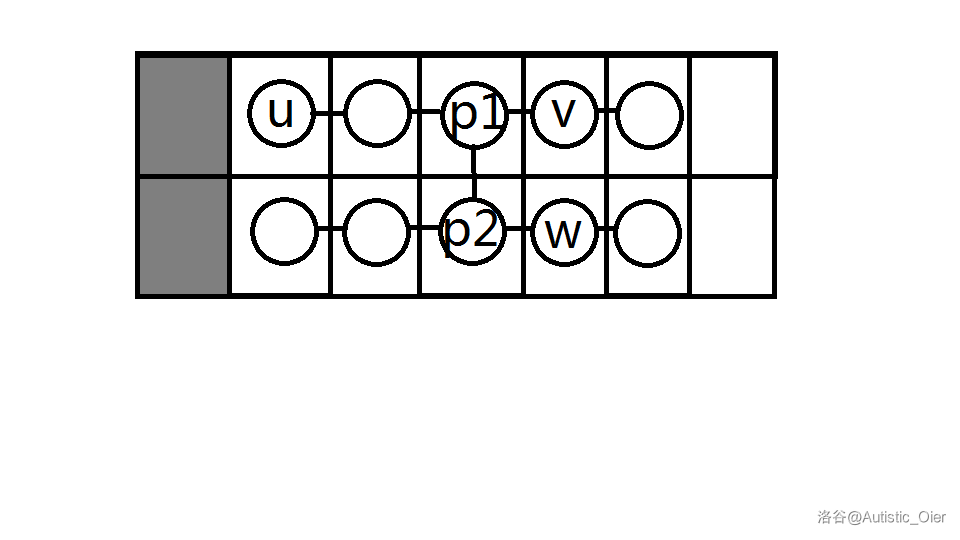
-
若 与 一个为较短的链,另一个在较短链的长度内都为链,也即有一条满足 的链,设齐平后较长链的对应儿子为 ,则 。
即:
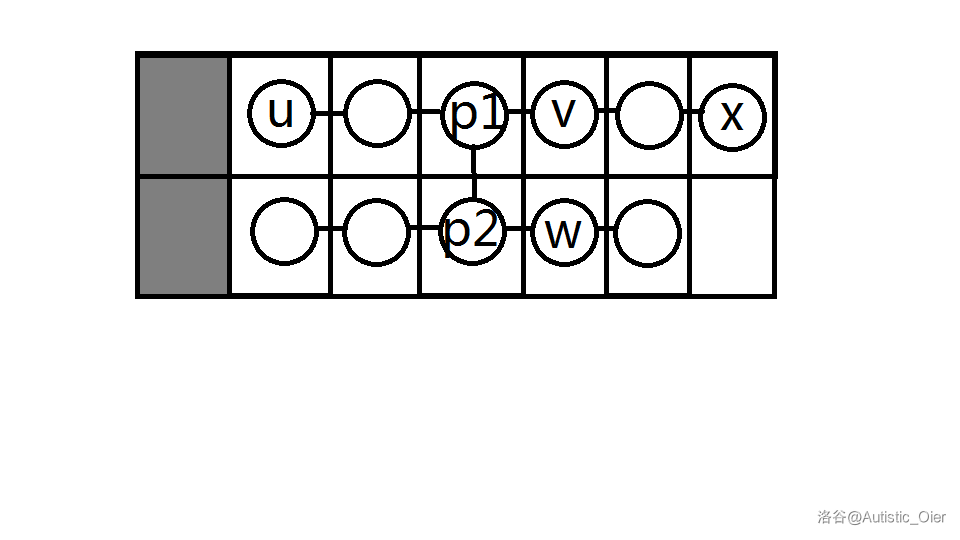
否则无法贡献答案。
-
-
-
-
-
最后考虑 有两个儿子的情况:(好累啊qwq)
需有一个儿子放在 下面,所以那个儿子不能有两个儿子。(上面是 ,左边和下面是墙,只能有一个在右边)
设 另一个儿子为 。
- 若其(设为 )没有儿子,显然有 。
即:
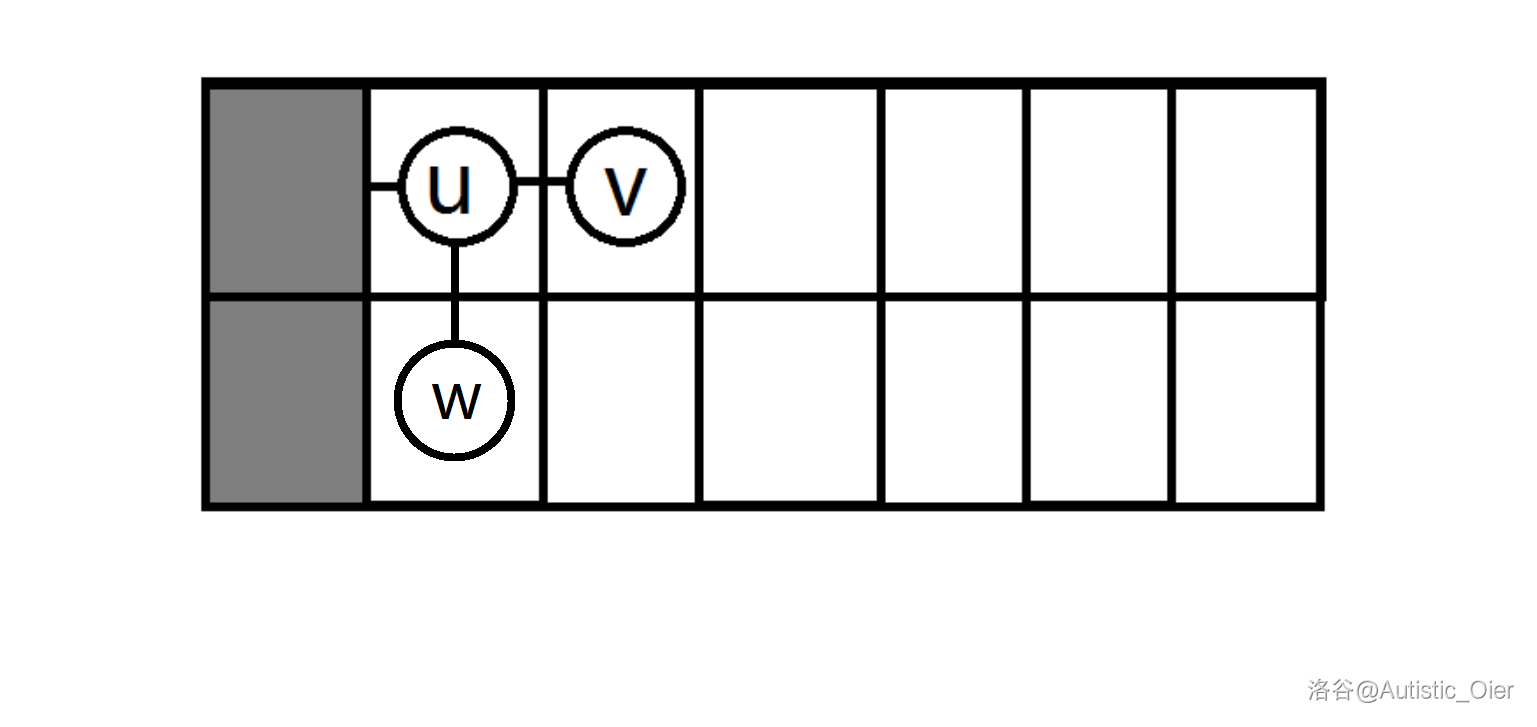
-
否则只有一个儿子,设其儿子为 ,发现与上文中:“ 的另一个儿子为 , 的另一个儿子为 ”的情况相同。即考虑是否为等长的链或是 一个较短链,另一个有比它长的链。(如果你足够懒,像我一样,就可以封一个函数处理这种情况)
还是放张图吧:
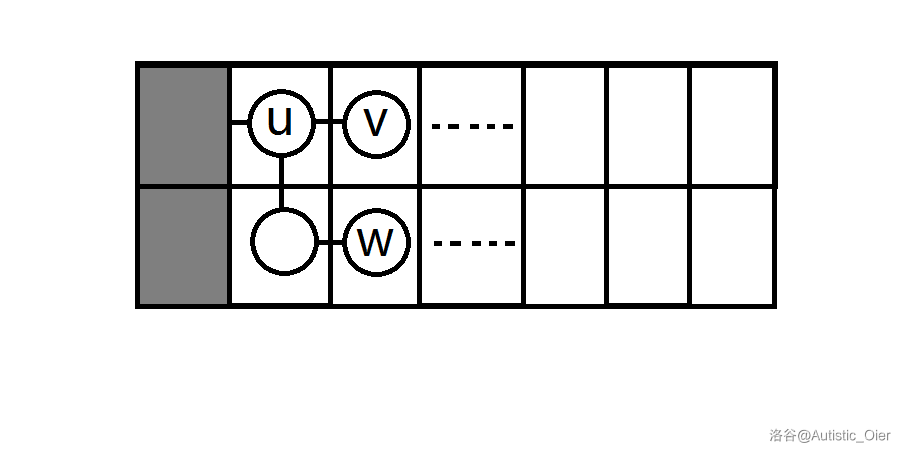
至于具体实现并不难,且只需 预处理出 与 ( 数组,用于处理取出链上/后的某点)即可讨论所有情况。
代码细节没有,只要将所有上述情况讨论完即可。
记得两个儿子中的一个要讨论,代码就不放了。
-
- 1
信息
- ID
- 3724
- 时间
- 4000ms
- 内存
- 500MiB
- 难度
- 6
- 标签
- 递交数
- 0
- 已通过
- 0
- 上传者
