自动搬运

查看原文

来自洛谷，原作者为

	xxasmcd 放下过去的痛，追逐未来的梦

搬运于2025-08-24 22:03:07，当前版本为作者最后更新于2021-11-28 15:25:03，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

对于这道题目给出一个例图：

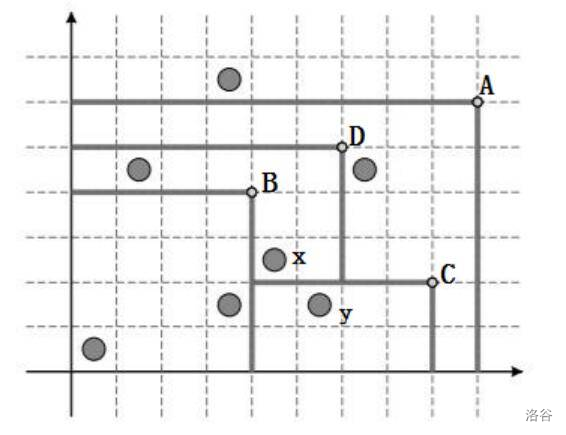
对于这个例图思路如下：

1. 每个栅栏先只计算只被本身覆盖的点（不被他的儿子覆盖，下面有儿子的定义）。例如上图 A 覆盖一个点，B 和 D 各覆盖两个点，C 覆盖一个点（怎么计算后面讲）。

2. 栅栏存在包含关系，B 被 D 包含（先不管 D 被 C 栅栏挡住了），D 和 C 都被 A 包含，如果计算 A 包含了多少个点，等价于 D 包含的 +C 包含的+只被 A 包含的三部分的和。这种包含关系形成树结构，树结构用父指针表示比较方便。

3. 栅栏有时间先后关系，B 是 D 的儿子，但是因为 B 先发生，D 后发生，所以 B 的答案不能传递累加到父亲 D 上；上图中 D 和 A 的先后顺序从图中判断不出来，如果 D 先发生 A 后发生，则 D 的答案也不能传递到父亲 A 上，但是如果是 A 先发生，则 D 的答案需要传递到父亲 A 上。也就是说儿子发生时间靠后才会影响父亲节点，所以应该按照发生顺序从后往前处理，使用并查集。

4. 怎么计算每个栅栏本身覆盖的点（不被儿子覆盖）？先对所有栅栏和点按照 y 轴由大到小排序。上图的 x 点能被直接被哪个栅栏覆盖？肯定是被他右上角的栅栏覆盖，所以用 set 维护已经处理的栅栏的横坐标，找到与 x 最接近且横坐标大于等于 x 点的栅栏 D，然后令 $cnt_{D}$ 加1。y 点貌似是被 D 覆盖，但是因为 C 在 D 之前发生，所以实际应该算是被 C 覆盖（D 比 C 先进入 set，因为 D 纵坐标大先处理），为了保证正确，在计算 C 栅栏时，把 C 插入 set，并且把 set 中横坐标小于 C 且发生时间在 C 之后的栅栏从 set 中删除，所以把 D 删除了，这样在处理 y 点时，set 中 C 与 y 最接近，所以 $cnt_{C}$ 加 1。

代码

#include<bits/stdc++.h>
using namespace std;
int n,m,fa[600001],cnt[600001],ans[600001],f[600001];
struct node
{
    int x,y,t;
}p[600010];
set<pair<int,int> > s;
int find(int x)
{
    if(x==f[x])return x;
    else return f[x]=find(f[x]);
}
bool cmp(node a,node b)
{
    if(a.y!=b.y)return a.y>b.y;
    else return a.t>b.t;
}
int main()
{
    cin>>n;
    for(int i=1;i<=n;i++)
    {
        cin>>p[i].x>>p[i].y;
        p[i].t=0;
    }
    cin>>m;
    for(int i=1;i<=m;i++)
    {
        cin>>p[i+n].x>>p[i+n].y;
        p[i+n].t=i;
    }
    sort(p+1,p+n+m+1,cmp);
    for(int i=1;i<=n+m;i++)
    {
        if(p[i].t==0)
        {
            set<pair<int,int> >::iterator it=s.lower_bound({p[i].x,p[i].t});
            if(it!=s.end())++cnt[it->second];
        }
        else
        {
            s.insert({p[i].x,p[i].t});
            set<pair<int,int> >::iterator it=s.find({p[i].x,p[i].t});
            if(++it!=s.end())fa[p[i].t]=it->second;
            while(1)
            {
                it=s.find({p[i].x,p[i].t});
                if(it==s.begin())break;
                it--;
                if(it->second>p[i].t)s.erase(it);
                else break;
            }
        }
    }
    for(int i=1;i<=m;i++)
    {
        f[i]=i;
    }
        for(int i=m;i>=1;i--)
        {
            ans[i]=cnt[find(i)];
            if(fa[i])
            {
                int x=find(i),y=find(fa[i]);
                f[x]=y,cnt[y]+=cnt[x];
            }
        }
    for(int i=1;i<=m;i++)
    {
        cout<<ans[i]<<endl;
    }
    return 0;
}