1 条题解
-
0
自动搬运
来自洛谷,原作者为

pythoner713
Hope deferred maketh the something sick.搬运于
2025-08-24 22:03:02,当前版本为作者最后更新于2021-01-28 19:55:32,作者可能在搬运后再次修改,您可在原文处查看最新版自动搬运只会搬运当前题目点赞数最高的题解,您可前往洛谷题解查看更多
以下是正文
转自我在知乎上写的文章,可以看一看呀:https://zhuanlan.zhihu.com/p/347566986
在欣赏一个有趣的数列前,我们需要引入一个图论概念:同构。
两图同构的意思是: 图的顶点可以经过一定的重新标号,使得它的点集和边集与 相同。 例如,以下两个图是同构的:
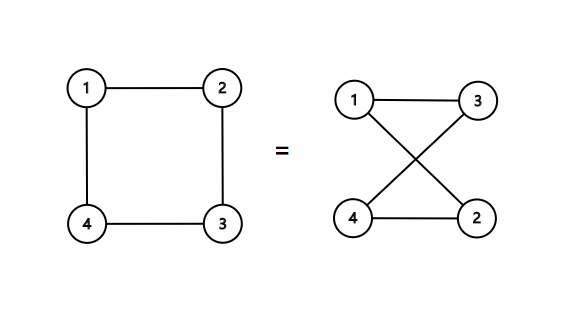
因为如果将左图的 (3,4) 两点交换,两图的点集和边集是相等的。
再如,对于有 个顶点的简单无向图,共有 种互不同构的图:
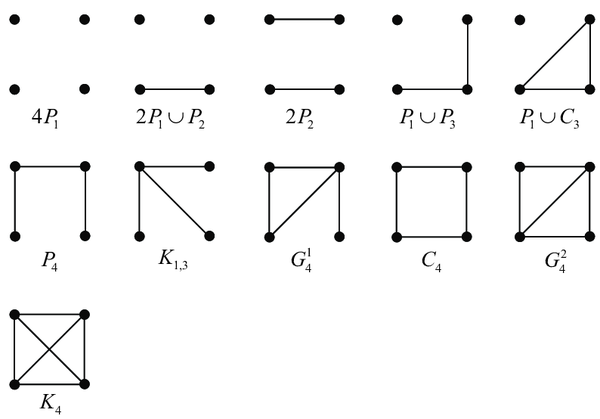
现在问题来了: 个顶点组成的简单无向图中,有多少种图互不同构?
这个问题的答案便是文章开头的数列——A000088。
为了解决这个问题,我们需要求助于数学的另一领域:群论。
将图的顶点重新标号,就相当于对点集进行置换,所有的标号方式便构成了一个置换群 。我们要求的即是在 作用下本质不同的图的个数。对于有 个顶点的图,所有的标号方式便是顶点的全排列,即 。
现在隆重请出 引理:
:集合 在群 作用下的轨道数(或本质不同元素数)
:在变换 下, 集合中的不动点数
这个定理对解决计数问题有重要作用,举个例子:

在本题中, 即为 个顶点可以构成的 个简单无向图的集合, 即为所求。难点在于怎么求 ,即对于某个点集置换 而言,有多少张图在经历变换 后依然和原来的图相同?
好了,让我们随机抽取一名幸运置换 进行研究,看看有多少张图在经历 后纹丝不动。
若隐若现的边太麻烦啦!不妨假设所有边都已存在,现在在我们面前的是一个 个节点的完全图,然后我们需要给边们染色,染成存在或不存在两种颜色,从而得到 中所有的图。
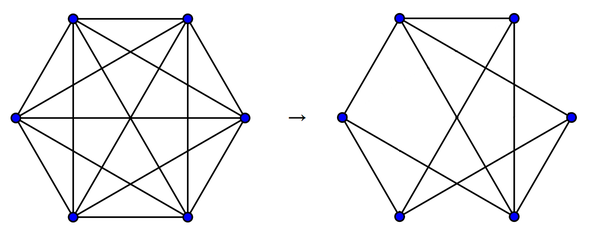
如何判断染成什么样子可以使得它成为置换 中的不动点呢?
注意到有些边是等价的,等价的边一定要染成同一个颜色,要么同时存在,要么同时不存在。
例如一个三个顶点的三角形,如果置换 的作用是将三个顶点顺时针轮换,那么这三条边是等价的(同属一个等价类),要么同时存在(形成一个完整的三角形),要么同时不存在(形成三个孤立的顶点)。不可能出现有两条边存在,一条边不存在的情况,否则经过一次旋转,缺口便到了另外两个点间,与原来的图就不同了。注意到此时三边同属 个等价类,每个等价类要么染要么不染,因此在此置换 下有 个不动点。
还是这个三角形,这回置换 变为交换两个点,另一个点不动。那么两个动点间的边单独属于一个等价类,另外两条边属于另一等价类,一共有 个等价类。每个等价类要么染要么不染,因此再此置换 下有 个不动点。
换句话说,对于置换 如果存在 个边的等价类,那么 中就有 个不动点。即:
好啦,接下来的问题就是求 ——置换 下边的等价类个数。这部分是关键,而且有些绕,我们分两步走:
第一步,我们要将 拆分为若干个不相交的循环置换。
这是什么意思呢?举个例子, 可以把点 置换成 ,可以记作: $g= \begin{pmatrix} 1 & 2 & 3 & 4 & 5 & 6\\ 2 & 3 & 1 & 5 & 4 & 6 \end{pmatrix}$ 。注意到这个置换可以分解成几个不相交的部分,其中每个部分都是一个循环:
$$\begin{pmatrix} 1 & 2 & 3 & 4 & 5 & 6\\ 2 & 3 & 1 & 5 & 4 & 6 \end{pmatrix}=\begin{pmatrix} 1 & 2 & 3\\ 2 & 3 & 1 \end{pmatrix} \circ \begin{pmatrix} 4 & 5\\ 5 & 4 \end{pmatrix} \circ \begin{pmatrix} 6\\ 6 \end{pmatrix} $$现在将我们当前研究的置换 拆成 个循环,长度分别为 。
第二步,将边按照端点分成两类
1.端点同时存在于同一循环内的边。设循环长度为 ,则次循环共有 个等价类。例如对于长度为 的循环置换 $\begin{pmatrix} 1 & 2 & 3 & 4 & 5 & 6\\ 2 & 3 & 4 & 5 & 6 & 1 \end{pmatrix}$ ,我们把这 个点排成正六边形:
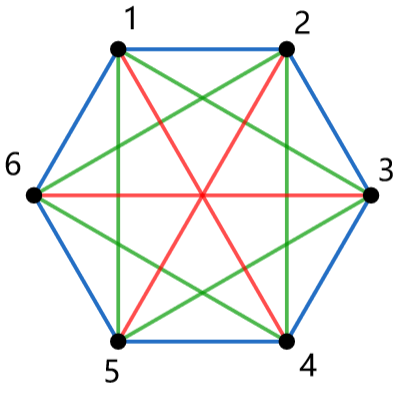
(颜色相同的边同属于一个等价类)
不难发现两条边等价当且仅当它们长度相等,等价的边必须同时染/不染,否则会导致图案不具有旋转对称性,经过循环置换后也必定与原图不同。而正 b 边形中,共有 种长度不同的线段,也就是对应 个边的等价类。得证。
因此这一类边一共贡献了 $\sum_{i=1}^K\left \lfloor \frac{b_i}{2} \right \rfloor$ 个等价类。
2.端点存在于不同循环内的边 。例如 $\begin{pmatrix} 1 & 2 & 3\\ 2 & 3 & 1 \end{pmatrix} \circ \begin{pmatrix} 4 & 5\\ 5 & 4 \end{pmatrix} \circ \begin{pmatrix} 6\\ 6 \end{pmatrix}$ ,则连接 的边不在同一循环内。这时,设两个循环的长度分别为 ,那么两个循环间共有 条这样的边。
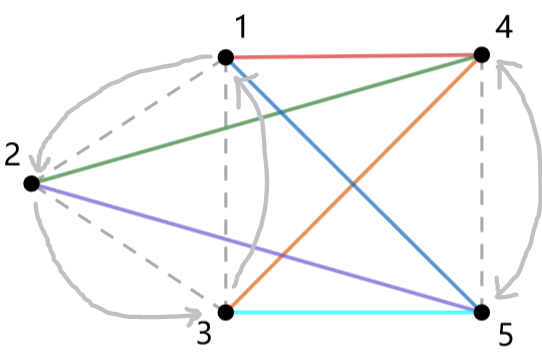
(如上图,循环 与 间共有 条边,但同属于 个等价类)
每条边经过 次循环后会回归原位,所以每个等价类大小为 。也就是说,一共有 个等价类。别忘了,这只是 内其中两个循环产生的贡献,要把每对循环的贡献累加起来,也就是: 个等价类。
至此两种情况已经分类讨论完毕,边的等价类个数就等于两种情况数量之和:
$$k=\sum_{i=1}^K\left \lfloor \frac{b_i}{2} \right \rfloor +\sum_{i=1}^K\sum_{j=1}^{i-1}\gcd(b_i,b_j) $$是不是感觉离成功不远了呢(
其实到了这里,我们已经找到计算文章开头数列的方法了。但是,别忘了 ,枚举每一个置换 ,时间复杂度少说也得 。我们是否以优化一下计算方法呢?
注意到有许多置换会被重复计算,如下面两个置换:
$$\begin{pmatrix} 1 & 2 & 3\\ 2 & 3 & 1 \end{pmatrix} \circ \begin{pmatrix} 4 & 5\\ 5 & 4 \end{pmatrix} \circ \begin{pmatrix} 6\\ 6 \end{pmatrix}\qquad\begin{pmatrix} 1 \\ 1 \end{pmatrix} \circ \begin{pmatrix} 2 & 3\\ 3 & 2 \end{pmatrix} \circ \begin{pmatrix} 4 & 5 & 6\\ 6 & 4 & 5 \end{pmatrix} $$它们间没有本质上的区别,对应的 值都相等(因为 都是 ),本可以统一计算。
一般地,如果两个置换的循环长度排序后一一相等,那么两者对答案的贡献 是相等的。因此,与其枚举每一种置换再拆分,不如枚举 的拆分代表一类置换,再统一计算贡献。 例如 时,它的拆分有 $(1,1,1,1,1),(1,1,1,2),(1,1,3),(1,2,2),(1,4),(2,3),(5)$ ,其中 统一代表了形如
$$\begin{pmatrix} * \\ * \end{pmatrix} \circ \begin{pmatrix} * & *\\ * & * \end{pmatrix} \circ \begin{pmatrix} * & *\\ * & * \end{pmatrix} $$的置换。也就是循环长度 的置换。
那么对于某个拆分,如何计算有多少对应的置换呢?
首先 随便放一共有 种方案,但长度为 的循环会贡献 倍重复方案。所以单是分配每个元素在哪个循环中就有 种方案。
接着是循环的内部分配,也就是 个元素的圆排列,有 种方案。
但事实上,对于长度相等的循环它们之间可以彼此交换,本质上是一样的,因此还是会算重。设 表示表某个长度的循环的个数,则会算重 倍。因此答案还需除以 。
结合上述三项,可以得到,拆分 所对应的置换个数为:
用这个式子改进之前的 n! 枚举算法,可以得到:
$$|X/G|=\frac{1}{|G|}\sum_b \frac{n!}{\prod(b_i)\prod(c_i!)} 2^k $$,里外两项正好抵消,得到最终的形式:
$$\large{|X/G|=\sum_b \frac{2^k}{\prod(b_i)\prod(c_i!)}} $$$$\large{k=\sum_{i=1}^K\left \lfloor \frac{b_i}{2} \right \rfloor +\sum_{i=1}^K\sum_{j=1}^{i-1}\gcd(b_i,b_j)} $$大功告成。
最后再提一下时间复杂度。DFS枚举 的拆分 ,再 求 。增长速度是 A000041,A296010 的乘积。前者增速是 ,后者不知道。估计总复杂度大概在 左右。
#include<bits/stdc++.h> #define int long long using namespace std; int ans, n, p = 997, b[70], jc[70], jd[70]; int gcd(int a, int b){ return !b ? a : gcd(b, a % b); } int qpow(int A, int B){ int C = 1; while(B){ if(B & 1) C = C * A % p; A = A * A % p, B >>= 1; } return C; } void init(){ jc[0] = 1; for(int i = 1; i < 70; i++){ jc[i] = i * jc[i - 1] % p; } // 预处理阶乘 } void work(int len){ int u = 0, v = 1; for(int i = 1; i <= len; i++){ u += b[i] >> 1; for(int j = 1; j < i; j++){ u += gcd(b[i], b[j]); } // 计算边的等价类个数,u 即题解的 k } for(int i = 1; i <= len; i++){ v = v * b[i] % p; } for(int i = 1, j; i <= len;){ for(j = i; b[i] == b[j] && j <= len; j++); v = v * jc[j - i] % p; // 去除长度相等的循环带来的重复计算 i = j; } ans = (ans + qpow(v, p - 2) * qpow(2, u) % p) % p; } void dfs(int now, int last, int rem){ if(!rem){ // DFS 枚举 n 的所有拆分 work(now - 1); return; } for(int i = last; i <= rem; i++){ b[now] = i; dfs(now + 1, i, rem - i); } } signed main(){ cin >> n; init(); dfs(1, 1, n); cout << ans; return 0; }不妨思考形式更一般的问题:
个节点的完全无向图,用 种颜色给每条边染色,可以染出几种互不同构的图?
答案十分简单,只需要将上述式子中的 2 改为 m 即可:
$$\large{|X/G|=\sum_b \frac{\color{red}{m}^\color{black}k}{\prod(b_i)\prod(c_i!)}} $$$$\large{k=\sum_{i=1}^K\left \lfloor \frac{b_i}{2} \right \rfloor +\sum_{i=1}^K\sum_{j=1}^{i-1}\gcd(b_i,b_j)} $$因为在原问题中,每条边有存在/不存在两种情况,这等价于用两种颜色给每条边染色,不动点数为 。现在改为用 种颜色染色,自然就是 了。
双倍经验:P4128
- 1
信息
- ID
- 3710
- 时间
- 2000ms
- 内存
- 125MiB
- 难度
- 7
- 标签
- 递交数
- 0
- 已通过
- 0
- 上传者
