15011418730 LV 7 @ 2025-8-24 22:03:00

自动搬运

来自洛谷，原作者为

	Piwry 空想上の人格保持者

搬运于2025-08-24 22:03:00，当前版本为作者最后更新于2020-07-05 20:23:07，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

~~建议还是只写个增量法够了~~

0.基础介绍

向量加减

同二维。

vect operator - (vect v){ return vect(x-v.x, y-v.y, z-v.z); }

向量点积（数值积）

同二维。

意义也和二维一样。

double operator * (vect v){ return x*v.x+y*v.y+z*v.z; }

向量叉积

vect operator / (vect v){ return vect(y*v.z-z*v.y, z*v.x-x*v.z, x*v.y-y*v.x); }

返回的是一个空间向量

它的默认方向和两个输入向量满足右手定理（形如三维坐标轴： $x$ 逆时针到 $y, z$ ， $y$ 逆时针到 $z$ 。返回的向量可以看做 $z$ 轴），

长度是输入向量构成的平行四边形面积，

正负由第一个向量到第二个向量的逆时针夹角决定（同二维），

不满足交换律

3b1b 中有对其含义的一种解释：将输入向量的起点置于原点，定义运算 $*$ 表示求一个点和输入向量构成的平行四边形构成的平行六面体的有向体积 $^1$ ，

那么做这个运算 $*$ 就相当于和输入向量的叉积（叉积方向为第一个叉第二个）做点积。

[1] 有向体积：设输入向量 $u, v$ ，原点 $O$ ，则有平面（具体存储规则见下） $(O, O+u, O+v)$ 。若点在平面上方则体积为正，否则为负。

向量模长

double m(){ return sqrt(x*x+y*y+z*z); }

投影到坐标面化简下式子就可以。

面的存储

struct plane{
	vect v[3];
	plane(){}
	plane(vect uu, vect vv, vect ww){ v[0] =uu, v[1] =vv, v[2] =ww; }
	vect normal(){ return (v[1]-v[0])/(v[2]-v[0]);}
};

存储面上的三个点。

若定义面的 "上方" 和 "下方"，则这三个点是按从上方看到的逆时针顺序排列的

其法向量（vect normal()）即为从一个点顺次连向后两个点的向量的叉积（顺次）。这个向量竖直指向面的上方。

判断点与面关系

inline bool isabove(vect v, plane p){ return gtr((v-p.u())*p.normal()/*这是投影长度乘法向量模长，只是因为不需要知道数值只需要符号，所以没做处理*/, 0); }

只需判断法向量起点到该点的这个向量在法向量上的投影符号即可。

点与面的距离

（这个在 quickhull 会用到）

/*带方向距离*/
inline double dist(vect v, plane p){ return (v-p.u())*p.normal()/p.normal().m(); }

法向量起点到该点的这个向量在法向量上的投影长。

多面体的储存

通常我们通过储存面来储存多面体。

对于多面体每个面的面积，我们可以用叉积的含义轻易算出：

plane facet;
double S =facet.normal().m()/2;/*其面积*/

（这一节从这往下，以及下一节 "地平线" 都是和 quickhull 有关的了，不感兴趣的可以跳过。本文介绍的前两个算法只需用数组单纯地存下平面即可）

在某些情况下，我们还需要存储每个面的邻接面信息。

为了方便，我们将每个顶点大于三个的面划分成若干个三角形的面；视具体情况可能划分后的面的顶点不属于原来面的顶点。

于是我们就可以这样保存面：

struct facet{
	int n[3];/*neighbor，和点对应 (u->v, v->w, w->u)*/
	plane p;
};

对于一个多面体，我们保存其中一个面作为索引，就可以通过邻接信息读取多面体的表面。

地平线

（貌似一般都叫 "Horizon"...直译过来就是地平线...）

对于一个点和一个多面体，从该点能 "看到" 的所有面一定是一片连续的面，而这片面的边缘就是这个点在这个多面体上的地平线。

地平线

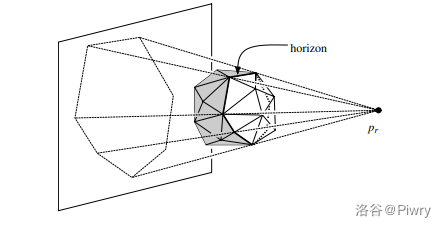
（可想象站在高处望向远处的场景...）

若要求得地平线，我们可以从某个该点能看到的面（具体来说就是这个面的平面在该点下面）开始 dfs（这个面也可以从索引面开始 dfs 求出），并在图中标记所有边缘面；

对于每个边缘面，我们将每条边缘边的两个顶点建图连边。

可以知道我们最后求出的图一定是一个环。

同时为了避免不必要的计算，我们可以在 dfs 顺便返回一个环上的一个点作为索引。

struct vect{
	double x, y, z;
	int id;
};

struct plane{
	vect vec[3];
};

struct facet{
	int n[3];
	int id, vistime /*相当于一个时间戳*/;
	plane p;
};

struct edge{
	int netid /*连向点的 id*/, facetid /*当前这条边缘边邻接的不可看见的面的 id*/;
};

bool isabove(vect v, plane p){ /*return (点是在面上方 );*/ }

vector<facet> FAC;/*存储所有面*/

int TIME =0;/*全局时间*/

/*e1 e2 存储一个点连的两条边，resfdel 存储所有看到的面，vistime 是每个点访问的时间戳*/
/*调用前需要更新时间 (++TIME)，清空 resfdel(至于 e1 e2 不清也没关系)*/
/*最后会返回边界线上的一个点，并保存地平线信息和所有能看到的面到指定数组*/
int getHorizon(int f, vect &p, int vistime[], edge e1[], edge e2[], vector<int> &resfdel){
	if(!isabove(p, FAC[f].p)) return 0;/*如果返回 0 则代表这个面无法看见*/
	if(FAC[f].vistime == TIME) return -1;/*如果返回 -1 则代表这个面已经见过*/
	FAC[f].vistime =TIME;/*记录当前时间戳*/
	FAC[f].isdel =1;
	resfdel.push_back(FAC[f].id);
	int ret =-2;/*如果返回 -2 则代表这个面的 dfs 树无法接触到地平线*/
	/*--(思考下 dfs 一个被夹在中心的面，周围一圈的面都已搜索过 )*/
	for(int i =0; i < 3; ++i){
		int res =getHorizon(FAC[f].n[i], p, vistime, e1, e2, resfdel);
		if(res == 0){
			int pt[2];
			pt[0] =FAC[f].p.vec[i].id, pt[1] =FAC[f].p.vec[(i+1)%3].id;
			for(int j =0; j < 2; ++j){
				/*我们无法得知这条边是沿缺口逆时针还是顺时针的*/
				/*根据被访问的次数判断这是该点连的第一条还是第二条边*/
				if(vistime[pt[j]] != TIME){
					vistime[pt[j]] =TIME;
					e1[pt[j]].netid =pt[(j+1)%2];
					e1[pt[j]].facetid =FAC[f].n[i];
				}
				else{
					e2[pt[j]].netid =pt[(j+1)%2];
					e2[pt[j]].facetid =FAC[f].n[i];
				}
			}
			ret =pt[0];
		}
		else if(res != -1 && res != -2) ret =res;/*保存地平线上的点*/
	}
	return ret;
}

多面体面与边的关系

我们可以想到，一条边会且仅会被两个面使用；按我们储存面的方式，这条边一定是被 "逆时针用一次"，再 "顺时针用一次"。

就像下图中那样：

凸包边

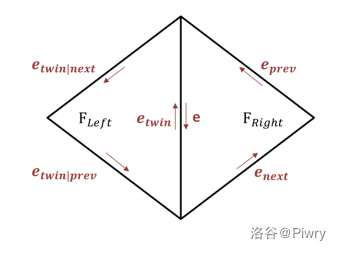
这个性质可以帮助我们通过统计边来获得多面体面的信息。

1.增量法

基本思路

我们考虑加入一个点时如何维护凸包

增量法1

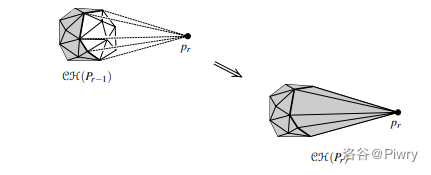
可以发现只有它能 "看到" 的面，或者说在该点下方的面（对于点恰好在面上，我们不算能 "看到"）会被删除。

所以初始先构造一个任意单纯形（四个顶点的多面体）。我们每加入一个点，就遍历所有面找出能看到的面，将它们删除；并对 "缺口" 的边缘边和新点连面，加入凸包。

求缺口边缘（地平线）

对于边缘的标记，我们可以想到：一条边会且仅会被两个面使用；按我们储存面的方式，这条边一定是被 "逆时针用一次"，再 "顺时针用一次"。（这里 copy 自上面）

于是用一个二维数组标记，只对只使用一次的边，按使用过的方向和新点连面即可（可见代码）。

对特殊情况的考虑

有时可能会出现几个点共面的情况。

我们考虑增量法的实现，可以发现在已有面上的点是无效的，也不会产生贡献。

不过由于我们连的面都是三角形，因此最后求得的面集合可能会把原来一个多边形面划分成多个三角形小面（同时也不保证三角形的顶点一定在边上）。注意后续运算需要考虑去重的问题。

另外，值得一提的是，如果我们通过扰动点（给点的坐标增减一个很小的数值）来期望最多使三个点共面，我们初始可以只构造面。这样可以略微缩减代码量。

不扰动的话这样可能出错。考虑这样的数据：

增量法2

由于扰动的值不需要太大，因此一般的精度要求用这种方法都可以满足。

CODE

扰动点（只构造面）：

#include <cstdio>
#include <cstdlib>
#include <cmath>

const int MAXN =2500;

/*------------------------------Computational geometry------------------------------*/

const double eps =1e-8;

struct vect{
	double x, y, z;
	vect(){}
	vect(double xx, double yy, double zz):x(xx), y(yy), z(zz){}
	vect operator - (vect v){ return vect(x-v.x, y-v.y, z-v.z); }
	vect operator / (vect v){ return vect(y*v.z-z*v.y, z*v.x-x*v.z, x*v.y-y*v.x); }
	double operator * (vect v){ return x*v.x+y*v.y+z*v.z; }
	double m(){ return sqrt(x*x+y*y+z*z); }
	double rd(){ return (rand()%2) ? eps : -eps; }
	void shake(){ x +=rd(), y +=rd(), z +=rd(); }
}pts[MAXN];

struct plane{
	int v[3];/*节省空间*/
	plane(){}
	plane(int uu, int vv, int ww){ v[0] =uu, v[1] =vv, v[2] =ww; }
	vect normal(){ return (pts[v[1]]-pts[v[0]])/(pts[v[2]]-pts[v[0]]); }
};

inline bool gtr(double a, double b){ return (a-b > eps); }

inline bool eq(double a, double b){ return (a-b > -eps && a-b < eps); }

inline double dist(vect x, vect y){ return (x-y).m(); }

inline double dist(vect v, vect f1, vect f2){ return ((f2-f1)/(v-f1)).m()/(f2-f1).m(); }

inline bool isabove(vect v, plane p){ return gtr((v-pts[p.v[0]])*p.normal(), 0); }

/*------------------------------Convex Hulls------------------------------*/

int vise[MAXN][MAXN];
plane res[MAXN<<1], del[MAXN<<1];

inline int getConvexHulls(int totp, plane facets[]){
	int s[3];
	s[0] =0, s[1] =1, s[2] =2;
	int totf =0;
	facets[totf++] =plane(s[0], s[1], s[2]);
	facets[totf++] =plane(s[0], s[2], s[1]);
	for(int i =0; i < totp; ++i){
		/*重复的点不会产生贡献*/
		int totr =0, totd =0;
		for(int j =0; j < totf; ++j){
			if(!isabove(pts[i], facets[j])) res[totr++] =facets[j];/*这里保存不需要删除的面*/
			else{
				del[totd++] =facets[j];
				/*由于每个点只会循环一次，所以这个 i+1 就相当于一个时间戳*/
				for(int k =0; k < 3; ++k)
					vise[facets[j].v[k]][facets[j].v[(k+1)%3]] =i+1;
			}
		}
		for(int j =0; j < totd; ++j){
			plane f =del[j];
			for(int k =0; k < 3; ++k)
				if(vise[f.v[k]][f.v[(k+1)%3]] == i+1 && vise[f.v[(k+1)%3]][f.v[k]] != i+1)
					res[totr++] =plane(f.v[k], f.v[(k+1)%3], i);
		}
		totf =totr;
		for(int j =0; j < totr; ++j) facets[j] =res[j];
	}
	return totf;
}

/*------------------------------Main------------------------------*/

plane facets[MAXN<<1];

int main(){
	int n; scanf("%d", &n);
	for(int i =0; i < n; ++i) scanf("%lf%lf%lf", &pts[i].x, &pts[i].y, &pts[i].z), pts[i].shake();/*扰动点*/
	int h =getConvexHulls(n, facets);
	double area =0;
	for(int i =0; i < h; ++i) area +=facets[i].normal().m()/2;
	printf("%.3lf", area);
}

不扰动点（仅给出不同部分）：

/*------------------------------Convex Hulls------------------------------*/

inline int getConvexHulls(int totp, plane facets[]){
	int s[4];
	s[0] =0, s[1] =1, s[2] =2, s[3] =0;
	while(s[2] < totp-1 && eq(dist(pts[s[2]], pts[s[0]], pts[s[1]]), 0)) ++s[2];/*确保不共线*/
	while(s[3] < totp-1 && eq(dist(pts[s[3]], plane(s[0], s[1], s[2])), 0)) ++s[3];/*确保不共面*/
	if(gtr(0, dist(pts[s[3]], plane(s[0], s[1], s[2])))) s[1] ^=s[2] ^=s[1] ^=s[2];/*为了保证下面构造的面向外*/
	int totf =0;
	facets[totf++] =plane(s[0], s[2], s[1]);
	facets[totf++] =plane(s[0], s[1], s[3]);
	facets[totf++] =plane(s[1], s[2], s[3]);
	facets[totf++] =plane(s[2], s[0], s[3]);
	
	/*...*/
	
	return totf;
}

/*------------------------------Main------------------------------*/

int main(){
	int n; scanf("%d", &n);
	for(int i =0; i < n; ++i) scanf("%lf%lf%lf", &pts[i].x, &pts[i].y, &pts[i].z);/*没有扰动*/
	
	/*...*/
	
	printf("%.3lf", area);
}

复杂度及其它

可以想到是 $O(n^2)$ 的。由于内部没有太多分支，常数应该不会太大。

这种做法可以很轻松地支持在线

2.卷包裹法（gift warp）

基本思路

我们想象用一张纸慢慢地包住凸包。

具体来说，我们想象有一个平面从凸包的一个面的一条边开始向内折，并取第一个碰到的点作为新的面的顶点，构造新面；这是一次打包（warp）。

我们再将新面新产生的两条边包含其面的信息（具体来说是边的方向，参考上文介绍的面与边的关系）放入队列，重复同样的工作，直到没有边可以再打包即可。

卷包裹1

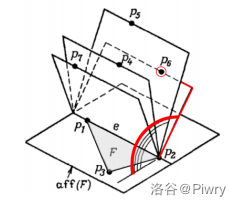
如何找到合适的点

比较直观的思路是求出所有点相对当前面的 "夹角"，不过这种方式难以实现。

我们再转化其含义，可以发现这实际上就是求一个新多边形面，使剩下的所有点都在新面下方（新面上方朝多面体外侧）。

/*单次打包*/
/*大部分变量名实例同上文*/
/*ne 是指当前边，边的方向保存了原来面的信息*/
pair<int, int> ne;/*存储两个顶点的 id*/
int p =-1;
for(int i =0; i < totp; ++i){
	if(i == ne.first || i == ne.second) continue;/*避免作为 p 的初始值 (p == -1)*/
	if(p == -1 || isabove(pts[i], plane(ne.first, ne.second, p)))
		p =i;
}

构建初始边

卷包裹法一开始需要一个属于最终凸包的边作为算法起点。

我们可以想到，如果将凸包 "拍平" 到一个平面上，其映射在平面上的点集的凸包的边一定也是原凸包的边。

初始边

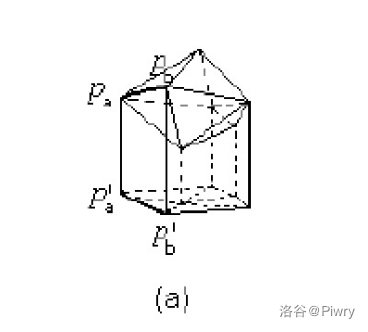
因此我们只需取某个坐标最大的点作为第一个点（它一定是凸包顶点），再将所有点拍平到某个面上（例如坐标面）按二维卷包裹法求一条相邻的边即可。

/*将 z 拍平的向量叉积*/
double mul2(vect u, vect v){ return u.x*v.y-u.y*v.x; }

/*将 z 拍平*/
inline bool onright(vect v, vect f1, vect f2){ return gtr(mul2(v-f1, f2-f1), 0); }

{/*求初始边*/
	int s[2];
	s[0] =0, s[1] =-1;
	for(int i =1; i < totp; ++i)
		if(gtr(pts[i].x, pts[s[0]].x))/*取 x 坐标最大的点*/
			s[0] =i;
	for(int i =0; i < totp; ++i){
		if(i == s[0]) continue;
		if(s[1] == -1 || onright(pts[i], pts[s[0]], pts[s[1]])/*点是否在直线 (拍平 )右侧*/)
			s[1] =i;
	}
}

卷包裹的共面难题

我们同样也考虑多个点共面的特殊情况。

首先可以想到一种比较 "友好" 的共面情况：

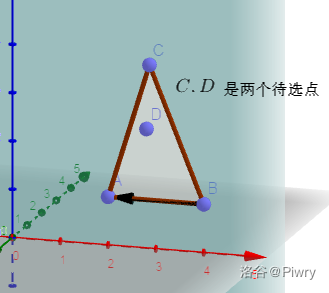
可以想到我们只需取和当前边所做三角形面积最大的的点就可以了。

但接下来再考虑这种情况：

共面F

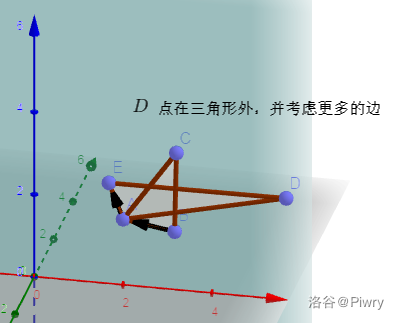
虽然我们对求得面要求并不严格，但这种重叠的面一定是不合法的。

或许可以想到将这些点映射到它们的平面上并求一次二维凸包，再一次性做它们面。由于每个点至多只会被带入做一次二维凸包，所以这种方法的复杂度是可以接受的。

但其代码复杂度难以想象...

相对而言更有效的方法是直接对点扰动，这样就可以直接不考虑共面的问题。

（如果有比映射求二维凸包更简洁的方法请务必联系我 QAQ）

CODE

（仅含有扰动实现的代码）

下面的代码进行了多次扰动。

主要原因是增量法只有在一开始有共面的危险（只用一个面做初始数据），但卷包裹法在每一次循环中都是要求不能超过三个点共面的。

#include <cstdio>
#include <cstdlib>
#include <cmath>
#include <algorithm>
using std::pair;
typedef pair<int, int> pad;

const int MAXN =2500;

/*------------------------------Computational geometry------------------------------*/

const double eps =1e-9;

struct vect{
	double x, y, z;
	vect(){}
	vect(double xx, double yy, double zz):x(xx), y(yy), z(zz){}
	vect operator - (vect v){ return vect(x-v.x, y-v.y, z-v.z); }
	vect operator / (vect v){ return vect(y*v.z-z*v.y, z*v.x-x*v.z, x*v.y-y*v.x); }
	double operator * (vect v){ return x*v.x+y*v.y+z*v.z; }
	double m(){ return sqrt(x*x+y*y+z*z); }
}pts[MAXN];

struct plane{
	int v[3];
	plane(){}
	plane(int uu, int vv, int ww){ v[0] =uu, v[1] =vv, v[2] =ww; }
	vect normal(){ return (pts[v[1]]-pts[v[0]])/(pts[v[2]]-pts[v[0]]); }
};

inline bool gtr(double a, double b){ return (a-b > eps); }

inline double dist(vect x, vect y){ return (x-y).m(); }

inline bool isabove(vect v, plane p){ return gtr((v-pts[p.v[0]])*p.normal(), 0); }

double mul2(vect u, vect v){ return u.x*v.y-u.y*v.x; }

/*将 z 拍平*/
inline bool onright(vect v, vect f1, vect f2){ return gtr(mul2(v-f1, f2-f1), 0); }

/*------------------------------Convex Hulls------------------------------*/

bool vise[MAXN][MAXN];
pad q[MAXN<<1]; int head, tail;

inline int getConvexHulls(int totp, plane facets[]){
	int s[2];
	s[0] =0, s[1] =-1;
	for(int i =1; i < totp; ++i)
		if(gtr(pts[i].x, pts[s[0]].x))
			s[0] =i;
	for(int i =0; i < totp; ++i){
		if(i == s[0]) continue;
		if(s[1] == -1 || onright(pts[i], pts[s[0]], pts[s[1]]))
			s[1] =i;
	}
	
	int totf =0;
	q[tail++] =pad(s[0], s[1]);
	q[tail++] =pad(s[1], s[0]);
	while(tail-head){
		pad ne =q[head++];
		if(vise[ne.first][ne.second]) continue;
		vise[ne.first][ne.second] =1;
		int p =-1;
		plane nf;
		for(int i =0; i < totp; ++i){
			/*避免当前边顶点作为 p 的初始值 (p == -1)，不然会导致面的三点共线*/
			if(i == ne.first || i == ne.second) continue;
			if(p == -1 || isabove(pts[i], nf))
				p =i, nf =plane(ne.first, ne.second, p);
		}
		facets[totf++] =nf;
		vise[ne.second][p] =vise[p][ne.first] =1;
		q[tail++] =pad(p, ne.second); q[tail++] =pad(ne.first, p);
	}
	return totf;
}

/*------------------------------Main------------------------------*/

plane facets[MAXN<<1];

double reps() {return (rand()/(double)RAND_MAX-0.5)*eps;}

int main(){
	int n; scanf("%d", &n);
	for(int i =0; i < n; ++i) scanf("%lf%lf%lf", &pts[i].x, &pts[i].y, &pts[i].z);
	/*具体扰动次数可以参考 :数据规模每增大 10 的次方扰动一次*/
	for(int k =0; k < 3; ++k) for(int i =0; i < n; ++i) pts[i].x +=reps(), pts[i].y +=reps(), pts[i].z +=reps();
	int h =getConvexHulls(n, facets);
	double area =0;
	for(int i =0; i < h; ++i) area +=facets[i].normal().m()/2;
	printf("%.3lf", area);
}

复杂度及其它

是 $O(nh)$ 的，其中 $h$ 是凸包点数；随机数据下减少的循环次数非常可观（自测了几个数据，大概是 $\sqrt n$ 的，仅供参考）

不过不知道为什么我写实现常数非常大，实际效率和我的增量法一样...（可能是因为过多的结构体构造）

这种做法是不支持在线的。

3. QuickHull

这种做法因为其和快速排序类似的启发式划分而得名。

（如果有人知道二维的 quickhull 的话，注意其实三维的 quickhull 和二维的区别还是蛮大的...）

基本思路

对于一个由最终凸包顶点组成的面和另一个点组成的棱锥，所有在其内部的点都是可以直接排除的。

具体来说，我们有一个均由最终凸包顶点组成的多面体 $H'$ ，其一个面（或面的划分，保证是一个三角形） $\pi$ ，和它被分配到的一个点集 $P_\pi$ 。

我们取离这个面最远的点，和多面体对于这个点的地平线连面更新多面体，可以获得多个新面 $F$ ，可以知道这些面的顶点一定是最终凸包的顶点；

将 $P_\pi$ 剩下的点加上被删除的面的点集 $P$ ，划分给 $F$ ，并保证每个点在划分到的面的上方**（注意一个点可能满足划分给多个面，而二维 quickhull 就不会有这种情况）；

对于不满足条件的点，就直接抛弃；

然后我们再将 $F$ 加入队列，继续处理下一个面（注意有时会处理到一个已经删除的面）。

可以参考这个流程图（不太好翻译，直接用原文可能更清晰）：

流程图

这里还有一个 quickhull 算法的 demo。

截图：

（可见面）

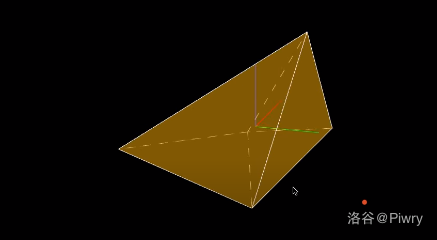
quickhull1

（地平线）

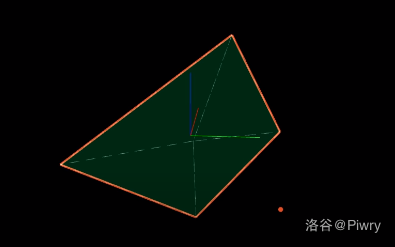
quickhull2

（新建面）

quickhull3

完整 demo 在这（baidu网盘，提取码：0eot）

初始化

为了找到一个由最终凸包的顶点组成的单纯形作为算法的开始，我们可以执行以下步骤：

我们首先分别在 $x, y, z$ 三个坐标轴方向上找到最大最小点，共 $3$ 对 $6$ 个点（这 $6$ 个点必在凸包上）；
在这 $6$ 个点当中，选取距离最大的两个点为初始点；
在这 $6$ 个点当中，选取距离第二步所选 $2$ 个点连线最远的点作为第 $3$ 个点；
遍历点集当中所有点，找到距离这 $3$ 个点所确定的平面最远的点作为第 $4$ 个点；

（来自）

这 $4$ 个点即是最初的单纯形。

然后我们再遍历所有点，给这个单纯形的四个面分配点即可。

CODE

代码是上面许多东西的综合（非常长）

思维难度和前两种方法差不多，但调试非常麻烦。

我的代码结构非常难看...还请见谅（暂时没啥时间改）；仅供参考思路。

（另外实现中删除面和流程图没严格对应，因为在查询地平线已经标记了删除的面，维护邻接信息时也抛弃了删除的面）

//输入退化为面或点未测试 
#include <cstdio>
#include <cmath>
#include <vector>
#include <list>
#include <queue>
using std::vector;
using std::list;
using std::queue;
using std::pair;
using std::max;
typedef pair<int, int> pad;

const int MAXN =2500;

/*------------------------------Computational geometry------------------------------*/

const double eps =1e-8;

struct vect{
	double x, y, z;
	int id;
	vect(){}
	vect(double xx, double yy, double zz):x(xx), y(yy), z(zz){}
	vect operator - (vect v){ return vect(x-v.x, y-v.y, z-v.z); }
	vect operator / (vect v){ return vect(y*v.z-z*v.y, z*v.x-x*v.z, x*v.y-y*v.x); }
	double operator * (vect v){ return x*v.x+y*v.y+z*v.z; }
	double m(){ return sqrt(x*x+y*y+z*z); }
};

struct line{
	vect u, v;
	line(){}
	line(vect uu, vect vv):u(uu), v(vv){}
};

struct plane{
	vect vec[3];
	plane(){}
	plane(vect uu, vect vv, vect ww){ vec[0] =uu, vec[1] =vv, vec[2] =ww; }
	vect normal(){ return (vec[1]-vec[0])/(vec[2]-vec[0]);}
	vect u(){ return vec[0]; }
};

inline bool gtr(double a, double b){ return a-b > eps; }

inline bool eq(double a, double b){ return (a-b > -eps && a-b < eps); }

inline bool eq(vect u, vect v){ return (eq(u.x, v.x) && eq(u.y, v.y) && eq(u.z, v.z)); }

inline double Abs(double x){ return gtr(0, x) ? -x : x; }

/*带符号距离*/
inline double dist(vect v, plane p){ return (v-p.u())*p.normal()/p.normal().m(); }

/*不带符号*/
inline double dist(vect v, line f){ return ((f.v-f.u)/(v-f.u)).m()/(f.v-f.u).m(); }

inline double dist(vect u, vect v){ return (u-v).m(); }

inline bool isabove(vect v, plane p){ return gtr((v-p.u())*p.normal(), 0); }

/*------------------------------Convex Hulls------------------------------*/

int TIME =0;/*全局时间戳*/

struct facet{
	int n[3];/*neighbor，和点对应 (u->v, v->w, w->u)*/
	int id, vistime/*访问的时间戳*/;
	bool isdel;
	plane p;
	facet(){ vistime =isdel =0; }
	facet(plane pp):p(pp){ vistime =isdel =0; }
	facet(int idd, plane pp):id(idd), p(pp){ vistime =isdel =0; }
	void in(int n1, int n2, int n3){ n[0] =n1, n[1] =n2, n[2] =n3; }
};

/*地平线的边*/
struct edge{
	int netid, facetid;
};

/*存储所有面*/
vector<facet> FAC;

struct ConvexHulls3d{
	int index/*索引面*/;
	double surfacearea;
	ConvexHulls3d(int indd):index(indd){ surfacearea =0; }
	
	void dfsArea(int nf){
		if(FAC[nf].vistime == TIME) return;
		FAC[nf].vistime =TIME;
		surfacearea +=FAC[nf].p.normal().m()/2;
		for(int i =0; i < 3; ++i)
			dfsArea(FAC[nf].n[i]);
	}
	
	double getSurfaceArea(){
		if(gtr(surfacearea, 0)) return surfacearea;
		++TIME;
		dfsArea(index);
		return surfacearea;
	}
	
	int getHorizon(int f, vect &p, int vistime[], edge e1[], edge e2[], vector<int> &resfdel){
		if(!isabove(p, FAC[f].p)) return 0;
		if(FAC[f].vistime == TIME) return -1;
		FAC[f].vistime =TIME;
		FAC[f].isdel =1;/*顺便标记删除的面*/
		resfdel.push_back(FAC[f].id);
		int ret =-2;
		for(int i =0; i < 3; ++i){
			int res =getHorizon(FAC[f].n[i], p, vistime, e1, e2, resfdel);
			if(res == 0){
				int pt[2];
				pt[0] =FAC[f].p.vec[i].id, pt[1] =FAC[f].p.vec[(i+1)%3].id;
				for(int j =0; j < 2; ++j){
					if(vistime[pt[j]] != TIME){
						vistime[pt[j]] =TIME;
						e1[pt[j]].netid =pt[(j+1)%2];
						e1[pt[j]].facetid =FAC[f].n[i];
					}
					else{
						e2[pt[j]].netid =pt[(j+1)%2];
						e2[pt[j]].facetid =FAC[f].n[i];
					}
				}
				ret =pt[0];
			}
			else if(res != -1 && res != -2/*被围在中间的面*/) ret =res;
		}
		return ret;
	}
};

/*----------------------------------------------------------------*/

/*全局点*/
vector<vector<vect> > pts;

/*构造初始单纯形*/
inline ConvexHulls3d getStart(vect point[], int totp){
	vect pt[6], s[4];
	for(int i =0; i < 6; ++i) pt[i] =point[1];
	/*取坐标轴最大点*/
	for(int i =2; i <= totp; ++i){
		if(gtr(point[i].x, pt[0].x)) pt[0] =point[i];
		if(gtr(pt[1].x, point[i].x)) pt[1] =point[i];
		if(gtr(point[i].y, pt[2].y)) pt[2] =point[i];
		if(gtr(pt[3].y, point[i].y)) pt[3] =point[i];
		if(gtr(point[i].z, pt[4].z)) pt[4] =point[i];
		if(gtr(pt[5].z, point[i].z)) pt[5] =point[i];
	}
	s[0] =pt[0], s[1] =pt[0], s[2] =pt[0], s[3] =pt[0];
	/*取距离最大的两个点*/
	for(int i =0; i < 6; ++i) for(int j =i+1; j < 6; ++j)
		if(gtr(dist(pt[i], pt[j]), dist(s[0], s[1])))
			s[0] =pt[i], s[1] =pt[j];
	/*取距离上两个点所连直线距离最远的点*/
	for(int i =0; i < 6; ++i)
		if(gtr(dist(pt[i], line(s[0], s[1])), dist(s[2], line(s[0], s[1]))))
			s[2] =pt[i];
	/*取所有点集中距离该面最远的点*/
	for(int i =1; i <= totp; ++i)/*!!*/
		if(gtr(Abs(dist(point[i], plane(s[0], s[1], s[2]))), Abs(dist(s[3], plane(s[0], s[1], s[2])))))
			s[3] =point[i];
	/*确保接下来构造的面是朝单纯形外的*/
	if(gtr(0, dist(s[3], plane(s[0], s[1], s[2])))){
		vect tmp =s[1]; s[1] =s[2]; s[2] =tmp;
	}
	/*构造单纯形*/
	int f[4];
	for(int i =0; i < 4; ++i) FAC.push_back(facet()), f[i] =FAC.size()-1, FAC[f[i]].id =f[i];
	FAC[f[0]].p =plane(s[0], s[2], s[1]),/*底面*/
	FAC[f[1]].p =plane(s[0], s[1], s[3]),
	FAC[f[2]].p =plane(s[1], s[2], s[3]),
	FAC[f[3]].p =plane(s[2], s[0], s[3]);
	FAC[f[0]].in(f[3], f[2], f[1]);
	FAC[f[1]].in(f[0], f[2], f[3]);
	FAC[f[2]].in(f[0], f[3], f[1]);
	FAC[f[3]].in(f[0], f[1], f[2]);
	/*给四个面分配点集空间*/
	for(int i =0; i < 4; ++i)
		pts.push_back(vector<vect>());
	/*给四个面分配点*/
	for(int i =1; i <= totp; ++i){
		if(eq(point[i], s[0]) || eq(point[i], s[1]) || eq(point[i], s[2]) || eq(point[i], s[3])) continue;
		for(int j =0; j < 4; ++j)
			if(isabove(point[i], FAC[f[j]].p)){
				pts[f[j]].push_back(point[i]);
				break;
			}
	}
	/*返回初始单纯形，以一个面作为索引*/
	return ConvexHulls3d(f[0]);
}

edge e[2][MAXN] /*边界线的图信息*/;
int vistime[MAXN] /*每个点访问的时间戳*/;
queue<int> que;
vector<int> resfnew /*保存新构造的面*/, resfdel /*保存删除的面*/;
vector<vect> respt /*保存需要分配的点*/;
inline ConvexHulls3d quickHull3d(vect point[], int totp){
	ConvexHulls3d hull =getStart(point, totp);
	/*将初始单纯形的面加入队列*/
	que.push(hull.index);
	for(int i =0; i < 3; ++i)
		que.push(FAC[hull.index].n[i]);
	/*snew 保存最后返回的凸包的索引面*/
	int snew =0;
	while(que.size()){
		int nf =que.front(); que.pop();
		/*当前面已被删除，跳过*/
		if(FAC[nf].isdel) continue;
		/*当前面没有分配到顶点，跳过*/
		if(pts[nf].size() == 0){
			snew =nf;/*确保面最后存在*/
			continue;
		}
		/*取距离该面最远的点*/
		vect p =pts[nf][0];
		for(int i =1; i < (int)pts[nf].size(); ++i)
			if(gtr(dist(pts[nf][i], FAC[nf].p), dist(p, FAC[nf].p)))
				p =pts[nf][i];
		/*求地平线，可以知道得到的地平线至少有三个点*/
		++TIME;
		resfdel.clear();
		/*当前面一定会被删除，因此直接从当前面 dfs*/
		int s =hull.getHorizon(nf, p, vistime, e[0], e[1], resfdel);
		/*遍历地平线（绕一圈），构造新面*/
		/*在求地平线时我们无法得知某条边是逆时针还是顺时针的，因此需要这里判断*/
		resfnew.clear();
		++TIME;
		int from =0 /*上一个访问的点*/, lastf =0 /*上一个新建的面*/, fstf =0 /*第一个新建的面*/;
		while(vistime[s] != TIME){
			/*用时间戳记录当前点是否访问*/
			vistime[s] =TIME;
			int net/*下一个点*/;
			int f /*地平线上当前边所接的无法看见的面*/, fnew /*新面*/;
			/*确保遍历方向正确*/
			if(e[0][s].netid == from) net =e[1][s].netid, f =e[1][s].facetid;
			else net =e[0][s].netid, f =e[0][s].facetid;
			/*求出这两个点在邻接面上的逆顺时针信息*/
			int pt1 =-1, pt2 =-1;
			for(int i =0; i < 3; ++i){
				if(eq(point[s], FAC[f].p.vec[i])) pt1 =i;
				if(eq(point[net], FAC[f].p.vec[i])) pt2 =i;
			}
			/*确保 pt1->pt2 是按邻接面的点的逆时针排列*/
			if((pt1+1)%3 != pt2) pt1 ^=pt2 ^=pt1 ^=pt2;/*交换*/
			/*这样构造的面是朝凸包外的*/
			FAC.push_back(facet(plane(FAC[f].p.vec[pt2], FAC[f].p.vec[pt1], p)));
			fnew =FAC.size()-1, FAC[fnew].id =fnew;
			pts.push_back(vector<vect>());
			resfnew.push_back(fnew);
			/*维护邻接信息*/
			FAC[fnew].n[0] =f, FAC[f].n[pt1] =fnew;
			if(lastf){
				/*不能预先确定是顺时针遍历还是逆时针遍历*/
				/*维护新建的面之间的邻接信息*/
				if(eq(FAC[fnew].p.vec[1], FAC[lastf].p.vec[0])) FAC[fnew].n[1] =lastf, FAC[lastf].n[2] =fnew;
				else FAC[fnew].n[2] =lastf, FAC[lastf].n[1] =fnew;
			}
			else fstf =fnew;/*还未新建面*/
			lastf =fnew;
			from =s;
			s =net;
		}
		/*给新建的面头尾维护临界信息*/
		if(eq(FAC[fstf].p.vec[1], FAC[lastf].p.vec[0])) FAC[fstf].n[1] =lastf, FAC[lastf].n[2] =fstf;
		else FAC[fstf].n[2] =lastf, FAC[lastf].n[1] =fstf;
		/*取得所有需要分配的点*/
		respt.clear();
		for(int i =0; i < (int)resfdel.size(); ++i){
			for(int j =0; j < (int)pts[resfdel[i]].size(); ++j)
				respt.push_back(pts[resfdel[i]][j]);
			pts[resfdel[i]].clear();
		}
		/*分配点*/
		for(int i =0; i < (int)respt.size(); ++i){
			if(eq(respt[i], p)) continue;/*跳过用于新建面的点*/
			for(int j =0; j < (int)resfnew.size(); ++j)
				if(isabove(respt[i], FAC[resfnew[j]].p)){
					pts[resfnew[j]].push_back(respt[i]);
					break;/*确保点不会被重复分配*/
				}
		}
		/*将新的面加入队列*/
		for(int i =0; i < (int)resfnew.size(); ++i)
			que.push(resfnew[i]);
	}
	hull.index =snew;
	return hull;
}

inline void preConvexHulls(){
	/*0 位做保留*/
	pts.push_back(vector<vect>());
	FAC.push_back(facet());
}

/*------------------------------Main------------------------------*/

vect point[MAXN];

int main(){
	preConvexHulls();
	int n; scanf("%d", &n);
	for(int i =1; i <= n; ++i){
		double x, y, z; scanf("%lf%lf%lf", &x, &y, &z);
		point[i] =vect(x, y, z);
		point[i].id =i;
	}
	ConvexHulls3d hull =quickHull3d(point, n);
	printf("%.3lf", hull.getSurfaceArea());
}

复杂度及其它

时间复杂度据说是期望 $O(nlogn)$ 的，最坏可能被卡到 $O(nh)$ 。常数可能较大。

空间复杂度是 $O(n)$ 的。

按我上面的实现,；我自己测试了下，开 O2， $10^6$ 的随机点大概可以跑到 $5s$ 左右（仅供参考）。

4. 一些闲话

这篇文章是真的长...

三维计算几何到处都是坑，真的建议只当兴趣学习（话说这东西只有 ZJOI2018 考到过一次吧（九条可怜），还只用增量法就行）。

如果对三维计算几何感兴趣的话还可以再去我博客看看。

ID

3677

时间

1000ms

内存

125MiB

难度

标签

递交数

已通过

上传者

Hydro

1 条题解

自动搬运

以下是正文

0.基础介绍

向量加减

向量点积（数值积）

向量叉积

向量模长

面的存储

判断点与面关系

点与面的距离

多面体的储存

地平线

多面体面与边的关系

1.增量法

基本思路

求缺口边缘（地平线）

对特殊情况的考虑

CODE

复杂度及其它

2.卷包裹法（gift warp）

基本思路

如何找到合适的点

构建初始边

卷包裹的共面难题

CODE

复杂度及其它

3. QuickHull

基本思路

初始化

CODE

复杂度及其它

4. 一些闲话

【模板】三维凸包

信息

1 条题解

自动搬运

以下是正文

0.基础介绍

向量加减

向量点积（数值积）

向量叉积

向量模长

面的存储

判断点与面关系

点与面的距离

多面体的储存

地平线

多面体面与边的关系

1.增量法

基本思路

求缺口边缘（地平线）

对特殊情况的考虑

CODE

复杂度及其它

2.卷包裹法（gift warp）

基本思路

如何找到合适的点

构建初始边

卷包裹的共面难题

CODE

复杂度及其它

3. QuickHull

基本思路

初始化

CODE

复杂度及其它

4. 一些闲话

【模板】三维凸包

信息

还没有账户？

登录