自动搬运

查看原文

来自洛谷，原作者为

	p878567 以下证明：这一算法的时空复杂度是 $o(+\infty)$

搬运于2025-08-24 22:02:47，当前版本为作者最后更新于2019-10-15 22:40:58，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

在正式写题解之前，先抨击一下已有的题解：

@Loi_bibo TLE

@Ofnoname $O(dn)$，显然TLE

@yi_heng 说是$O(n)$的，实际上可以卡成$O(n^2)$，具体卡法见附注。

@lokiii 证明和结论都是错的，卡法见附注。

出题人的数据真弱

现在说我的解法：放心，下面两个都能通过，如果再次被卡可以用各种手段告知我

实际上前面几份题解虽然是错的，但找出最短距离并枚举这一段上的起点是必要的，这里要解决的是怎样用$O(n/d)$的时间（前面的问题就是用$O(n)$的时间）统计分割点的最小数量，这样就能保证复杂度为$O(n)$。

不妨设最短点对是$1\sim d$，并记连接$i$与$i+1$（$\!\mod 2n$意义下，下同）的弧编号为$i$。假定我们选择从$i$（弧）处断开，那么由最短性可知$1\sim i-1$的弧无需断开，因此仅需考虑$i\sim2n$的弧。这个问题的$O(n)$做法可以贪心（断开处必选，其余位置尽可能后移），考虑维护这个贪心。

首先断开弧$2n$（但不是完全断开，见下）

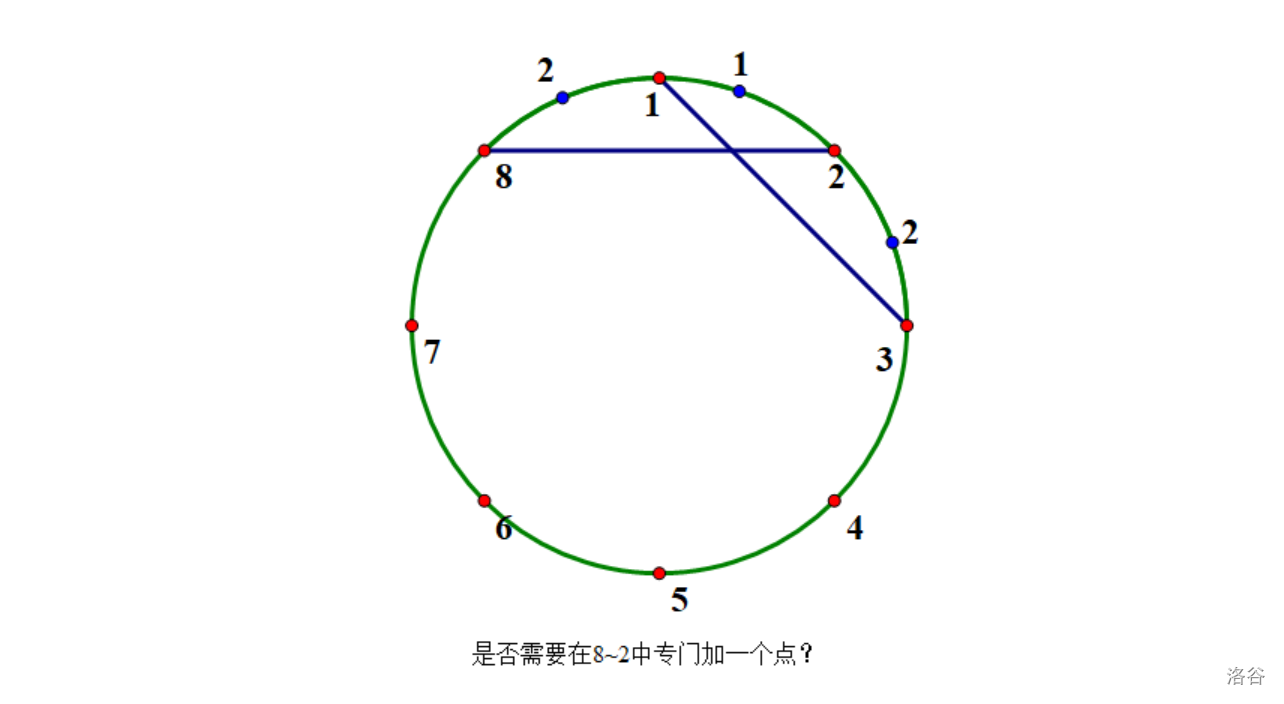
从该分割线起，所有边均指不包含弧$n$的部分

引理：设边$(l1,r1)$，$(l2,r2)$满足$l1<l2<r1<r2$，则删除边$(l1,r1)$对答案无影响。

这是因为边$(l2,r2)$中有分割点时边$(l1,r1)$中一定有分割点。

这样，我们可以过滤掉可以对答案无影响的边，这样就能按两端点同时增序枚举这些边。

定义$f_i$表示按照贪心策略在弧$i$上选取分割点后（假设所有左端点小于等于$i$的弧上均已有分割点），下一个分割点的位置。

考虑相邻的两条边$(l1,r1)$,$(l2,r2)$，那么编号在$[l1,l2)$的弧对应的$f$值为$r2-1$。（画个图理解一下）

我们考虑按编号从$1$到$d-1$的顺序枚举第一个分割点。那么这个分割点前面是找不到完整的一条边的（否则$d$就不是最短距离了），这样每次从$i$跳到$f_i$，复杂度为$O(n/d)$（即分割点的数量上限），完结。

其实还差一点：我们错误地忽略了包含弧$2n$的边。

如果两端点都不在$[1,d]$的范围内，显然不用考虑。

如果都在，这是不可能的。

假定在$[1,d]$范围内的端点编号为$x$，那么$x>i$时不用考虑，把$x=i$的边插入后维护$f$多出的最后一段即可。

由于$f$中的每一个值只会被求一次，因此复杂度是$O(n)$的。

代码：

#include<bits/stdc++.h>
using namespace std;
int read() {
	char c=getchar();while(!isdigit(c))c=getchar();
	int num=0;while(isdigit(c))num=num*10+c-'0',c=getchar();
	return num;
}
int m[1000001];
int f[400001];
int main() {
	int n = read();
	int dis = n * 2, lp, rp;
	for (int i = 1; i <= n; i++) {
		int a, b;
		a = read(), b = read();
		if (a > b) swap(a, b);
		m[a]=b, m[b]=a;
		m[a+n*2]=b, m[b+n*2] = a;
		if (b - a < dis)
			dis = b - a, lp = a, rp = b;
		if (a + n * 2 - b < dis)
			dis = a + n * 2 - b, lp = b, rp = a + n * 2;
	}
	for (int i = 1; i <= n * 2; i++) m[i]=m[i+lp-1];
	int d = rp - lp + 1;
	int pt = 0, last = 1;
	for (int i = d + 1; i <= n * 2; i++)
		if (m[i] < i && m[i] > last) {
			for (int j = last; j < m[i]; j++) f[j] = i - 1;
			last = m[i];
		}
	int ans = n;
	for (int i = 1; i < d; i++) {
		if (m[i] > last) {
			for (int j = last; j < m[i]; j++) f[j] = n * 2;
			last = m[i];
		}
		int p = i, cnt = 0;
		while (p) {
			p = f[p];
			++cnt;
		}
		ans = min(ans, cnt);
	}
	cout << (ans + 1) / 2 << endl;
}

附注：

1.卡掉@yi_heng的数据：

#include<bits/stdc++.h>
using namespace std;
int main() {
	int n = 200000;  //必须是偶数
	cout << n << endl;
	cout << 1 << ' ' << n / 2 + 1 << '\n';
	cout << n + 1 << ' ' << n * 3 / 2 + 1 << endl;
	int p = 2, q = n + 2;
	while (p <= n / 2) cout << p++ << ' ' << q++ << endl;
	p = n / 2 + 2, q = n * 3 / 2 + 2;
	while (p <= n) cout << p++ << ' ' << q++ << endl;
}

2.卡掉@lokiii的数据：

10
1 6
5 10
11 16
15 20
2 9
3 8
4 7
12 19
13 18
14 17

正解：1，输出：2