自动搬运

查看原文

来自洛谷，原作者为

	Seauy I remember your song, sung by centuries of wind.

搬运于2025-08-24 22:02:19，当前版本为作者最后更新于2019-03-04 21:33:08，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

既然没有人写题解，那我就首当其冲吧

这道题方法其实很多

先说明一点，每次可以从 A类 获得 a 的权值，从 B类 获得 b，最小的情况是 min(a,b)，题目要我们求的就是最大的 min(a,b)

第一眼看上去就像动态规划，但是具体怎么规划我不知道

但是有一点确定，动态规划的朋友们，数据给你的权值要乘以 10^4 不然无法规划，数组也要开到原来的 10^4 倍

好了废话到此为止，重头戏现在开始

法一：三分法

这其实是这道题的正解

三分法，名字十分形象，跟二分法很类似，只不过它是每次三等分，有些情况会比二分快

比如这道题，其实二分根本做不了，只能用三分

为什么呢？大家都知道，二分的前提是数据呈单调上升，这样我们才能把一条图像分成大与小两部分

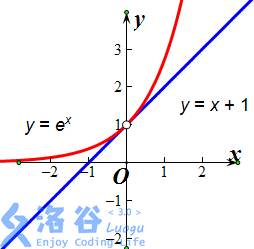类似于这种图像，是二分所适用的，因为纵着切一刀可以分成大小一眼可辨的大与小两瓣

但是很显然，因为受“每拿一个灯泡就要耗费一权值”的限制，函数不呈单调上升，那是什么样呢？

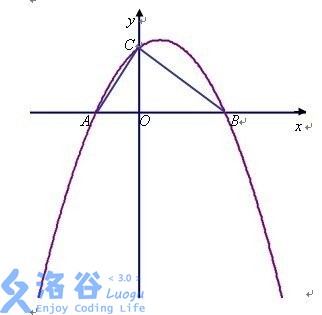
是类似的二次函数，满足规律“先上升再下降”（二次函数性质易证）

而我们要求的答案自然在最高处的“屈服点”

而我们用三分法对答案进行试探，每次三分必然产生“左，中，右”三段，而再进一步分析左中右的走势再判断屈服点在那一段

具体说，我们找到了两个点，a 与 b，把这一段分成了三段

1. a<=b时，答案则锁定在中与右段，则继续三分 a~R 段

2. a>b 时，答案则锁定在左与中段，则三分 L~b 段

具体代码就不展示了，因为我不是用三分过的 qwq

法二：贪心（枚举）

我是用这个神奇算法过的，没有三分那么高大上

由于每一次都要花费一权值，那么高权值的灯泡不拿白不拿，那就全拿上了！

然而并不能很粗暴地全拿光，因为有可能好灯泡不是在 A类 与 B类 均匀分布的

所以更好的方法，是从 A类 拿一个贼大的，然后再从 B类 拿一堆尽量与 A 所获得的价值屏平衡

B 比 A 获得的多的时候，A 就不能坐以待毙了，要开始拿灯泡了

其实就是不断调整 A 与 B 获得的价值，使他们尽量平均

奉上代码（终于啊）

/*
    n 个 A组 灯泡
    n 个 B组 灯泡
    你在其中任意选灯泡（每个灯泡有它的价值）
    每选一个要用一块钱
    选完之后任意点亮已选的 A 或 B 灯泡
    你会得到相应的价值
    求最大的最小收益
    (A 类得 a ，B 类得 b，求最大的min(a,b))
*/
#include<bits/stdc++.h>
using namespace std;

int n;
double A[100001],B[100001],ans;
bool visit[100001][2];

bool cmp(double a,double b)
{return a>b;}

int main()
{
    scanf("%d",&n);
    for(int i=1;i<=n;i++) cin>>A[i]>>B[i];
    sort(A+1,A+n+1,cmp);
    sort(B+1,B+n+1,cmp);
    double a=0.0,b=0.0;
    for(double i=1,j=1;i<=n && j<=n;)
    {
        int x=i,y=j;
        a+=A[x]*double(!visit[x][0]);
        b+=B[y]*double(!visit[y][1]);
        visit[x][0]=visit[y][1]=1;
        ans=max(ans,min(a-i-j,b-i-j));
        if(a>=b) j++;
        if(a<=b) i++;
    }
    printf("%.4lf",ans);
    return 0;
}

话说这道题又不难，怎么没人写题解呢QAQ