自动搬运

查看原文

来自洛谷，原作者为

	xtx1092515503 Mathematics compares the most diverse phenomena, and discovers the secret analogies which unite them. @Joseph Fourier

搬运于2025-08-24 22:02:15，当前版本为作者最后更新于2020-07-07 16:35:36，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

方法来自于djq神仙

对偶图什么的是不会的，这辈子都是不会的

我们把一个房间（四面都有墙的极小密闭空间）抽象成一个节点，并在由一堵墙隔开的两个房间之间连一条边。

我们把城市外围也抽象成一个节点。则从该节点出发，搜出到每个房间的距离。则如果一堵墙两侧的房间到城市外围的距离相等，这堵墙便不会被冲塌。

但是这个方法太恶心了，因为你连各个房间由哪些墙组成都很难找出

所以就有一种方法：

我们把一堵墙拆成两个点$i$与$i'$，分别表示墙两侧的连通块；

在每个点处，我们合并它所连接着的墙所对应的连通块。

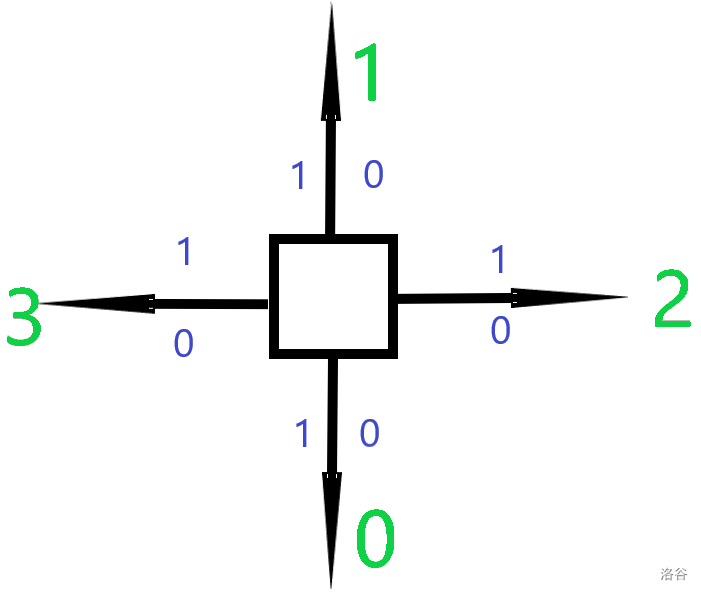
我们将四个方向分别定为$0,2,1,3$（绿字），同时令$0$表示$i$，$1$表示$i'$（蓝字）。则我们要合并$(\color{green}{0}\color{blue}0\color{black},\color{green}{2}\color{blue}0\color{black})$、$(\color{green}{2}\color{blue}1\color{black},\color{green}{1}\color{blue}0\color{black})$、$(\color{green}{1}\color{blue}1\color{black},\color{green}{3}\color{blue}1\color{black})$、$(\color{green}{3}\color{blue}0\color{black},\color{green}{0}\color{blue}1\color{black})$。当然，也有可能一个点并不在四个方向都有墙——那也不要紧，我们就跳过缺失的墙即可。

而怎么合并呢？你可能会直观地想到并查集——但是我们可以使用01bfs。我们可以在合并的点之间连上一条权值为$0$的边，并在墙所拆成的两个点之间连一条权值为$1$的边，然后搜索即可。

则一堵墙可以保留，当且仅当其被拆出的两个点到起点距离相等。

最后，我们如何找到代表城市外围的点呢？

抱歉，这个方法就不太美妙了——对于原图中每个连通块，找到里面$y$最大的那堵墙，则它拆出来的某个点一定在城市外围上，找到那个点作为bfs起点即可。

代码：

#include<bits/stdc++.h>
using namespace std;
int n,m,head[400100],cnt,dir[100100][4],to[100100][4],x[100100],y[100100],S,mxy,dis[400100],tot;
bool vis[100100];
struct edge{
	int to,next,val;
}edge[1001000];
void ae(int u,int v,int w){
//	printf("%d %d %d\n",u,v,w);
	edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=w,head[u]=cnt++;
	edge[cnt].next=head[v],edge[cnt].to=u,edge[cnt].val=w,head[v]=cnt++;
}
int ori(int u,int v){
	if(y[u]==y[v])return x[u]>x[v];
	if(x[u]==x[v])return 2+(y[u]>y[v]);
}
void dye(int u){
	vis[u]=true;
	for(int i=0;i<4;i++){
		if(!dir[u][i])continue;
		if((i==0||i==2)&&y[u]>mxy)mxy=y[u],S=dir[u][i];
		if(!vis[to[u][i]])dye(to[u][i]);
	}
}
void bfs(){
	deque<int>q;
	q.push_back(S),dis[S]=0;
	while(!q.empty()){
		int u=q.front();q.pop_front();
//		printf("%d:%d\n",u,dis[u]);
		for(int i=head[u];i!=-1;i=edge[i].next){
			if(dis[edge[i].to]<=dis[u]+edge[i].val)continue;
//			printf("%d->%d:%d\n",u,edge[i].to,edge[i].val);
			dis[edge[i].to]=dis[u]+edge[i].val;
			if(edge[i].val)q.push_back(edge[i].to);
			else q.push_front(edge[i].to);
		}
	}
}
int main(){
	scanf("%d",&n),memset(head,-1,sizeof(head)),memset(dis,0x3f3f3f3f,sizeof(dis));
	for(int i=1;i<=n;i++)scanf("%d%d",&x[i],&y[i]);
	scanf("%d",&m);
	for(int i=1,u,v;i<=m;i++){
		scanf("%d%d",&u,&v);
//		printf("U,V:%d V,U:%d\n",ori(u,v),ori(v,u));
		dir[u][ori(u,v)]=i,to[u][ori(u,v)]=v;
		dir[v][ori(v,u)]=i,to[v][ori(v,u)]=u;
		ae(i,i+m,1);
	}
	for(int i=1;i<=n;i++){
		vector<int>v;
		if(dir[i][0])v.push_back(0);
		if(dir[i][2])v.push_back(2);
		if(dir[i][1])v.push_back(1);
		if(dir[i][3])v.push_back(3);
		if(v.empty())continue;
		int p,q;
		for(int j=0;j+1<v.size();j++){
			p=v[j],q=v[j+1],ae(dir[i][p]+(p==1||p==2)*m,dir[i][q]+(q==0||q==3)*m,0);
		}
		p=v.back(),q=v.front(),ae(dir[i][p]+(p==1||p==2)*m,dir[i][q]+(q==0||q==3)*m,0);
	}
	for(int i=1;i<=n;i++){
		if(vis[i])continue;
		S=0,mxy=-1;
		dye(i);
		if(S)bfs();
	}
	for(int i=1;i<=m;i++)tot+=(dis[i]==dis[i+m]);
//	for(int i=1;i<=2*m;i++)printf("%d:%d\n",i,dis[i]);
	printf("%d\n",tot);
	for(int i=1;i<=m;i++)if(dis[i]==dis[i+m])printf("%d\n",i);
	return 0;
}