自动搬运

查看原文

来自洛谷，原作者为

	Seauy I remember your song, sung by centuries of wind.

搬运于2025-08-24 22:02:05，当前版本为作者最后更新于2020-07-06 16:44:47，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

一看任务跟输入就可以认定是个数据结构题

再看一眼数据范围，就可以猜到大概要用线段树维护

那么接下来我们就得分析题目来确定线段树要维护什么、怎么维护了

首先我们要确定一个四面体，我们能用哪些信息来描述它

最重要的信息就应该是 A 面的位置了

我们要记录四面体向前的方向吗？实际上是不需要的，我们可以认为一个四面体翻转完了之后，立即又把改变了方向的“向前方向”对准了朝北的方法，这么做是不会影响答案的

四面体有四个面，三维的不好考虑，我们把它“降维打击”

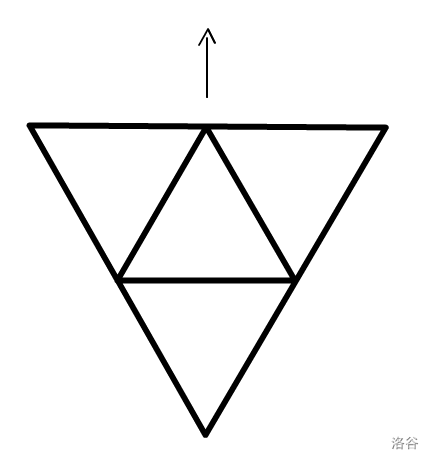
箭头方向就是“向前方向”

中间的三角形为三面体与地面接触的一面

A 可以放置在四个面的其中任意一个，那么四面体就有四种状态

下面的红字是对于每个状态的编号

通过观察发现，对于每个状态进行 L R B 操作会得到如下表格

[ 过程比较繁琐，有兴趣可以自己推导 ]

这是进行一次翻转操作获得的最终状态的表格

不用找规律，因为找到了也没啥用没有交换律

对于没有交换律的运算，可以用线段树处理出每个状态经过时间 $[L,R]$ 所有操作获得的结果，也就是获得 $f_{L,R}(x)$，这个函数是符合结合律的，也就是说可以合并 $[L,mid],[mid+1,R]$ 从而得到 $[L,R]$ 的结果

也就是满足如下公式

$f_{L,R}(x)=f_{mid+1,R}(ope_{mid}(f_{L,mid}(x)))$

状态处理好了，那 A 字面朝下的次数怎么统计呢？

用函数 $sum_{L,R}(x)$ 表示状态 x 经过 $[L,R]$ 所有操作时 A 字面朝下的次数，也就是得到状态 0 的次数

同样满足结合律，用线段树维护

那么最终，我们只要先算出 $beg=f_{1,L}(0)$ 再代入得出 $sum_{L,R}(beg)$ 就行了

上代码

#include<bits/stdc++.h>
#define mid ((L+R)>>1)
#define Lson (now<<1)
#define Rson (now<<1|1)
using namespace std;

const int MAXN=6e4;
const int MAXM=15e4;

struct SegTree
{
	int f[4];
	int sum[4];
	void Clean()
	{
		for(int i=0;i<4;i++) f[i]=i;
		sum[0]=1;
		for(int i=1;i<4;i++) sum[i]=0;
	}
}node[(MAXN<<2)+5];

int n,m;
int A[MAXN+5];
int mapn[4][3];

int Code(char x)
{
	if(x=='L') return 0;
	if(x=='R') return 1;
	return 2;
}

SegTree PushUp(SegTree a,int x,SegTree b)
{
	SegTree cnt;cnt.Clean();
	for(int i=0;i<4;i++)
	{
		cnt.f[i]=b.f[mapn[a.f[i]][A[x]]];
		cnt.sum[i]=a.sum[i]+b.sum[mapn[a.f[i]][A[x]]];
	}
	return cnt;
}

void Build(int now,int L,int R)
{
	if(L==R)
	{
		node[now].Clean();
		return;
	}
	Build(Lson,L    ,mid);
	Build(Rson,mid+1,R  );
	node[now]=PushUp(node[Lson],mid,node[Rson]);
}

void Change(int now,int L,int R,int x)
{
	if(L==R) return;
	if(x<=mid) Change(Lson,L,mid,x);
	else Change(Rson,mid+1,R,x);
	node[now]=PushUp(node[Lson],mid,node[Rson]);
}

void Assis(int x,int v)
{
	A[x]=v;
	Change(1,1,n+1,x);
}

SegTree Ask(int now,int L,int R,int QL,int QR)
{
	if(QL<=L && R<=QR) return node[now];
	if(QL<=mid && mid<QR) return PushUp(Ask(Lson,L,mid,QL,mid),mid,Ask(Rson,mid+1,R,mid+1,QR));
	if(QR<=mid) return Ask(Lson,L,mid,QL,QR);
	return Ask(Rson,mid+1,R,QL,QR);
}

int main()
{
	mapn[0][0]=mapn[0][1]=mapn[0][2]=3;
	mapn[1][1]=mapn[2][2]=mapn[3][0]=1;
	mapn[1][2]=mapn[2][0]=mapn[3][1]=2;
	scanf("%d",&n);
	char c;
	for(int i=1;i<=n;i++)
	{
		cin>>c;
		A[i]=Code(c);
	}
	Build(1,1,n+1);
	scanf("%d",&m);
	bool t;
	for(int L,R,beg;m--;)
	{
		cin>>t;
		if(t)
		{
			scanf("%d %d",&L,&R);
			beg=Ask(1,1,n+1,1,L).f[0];
			printf("%d\n",Ask(1,1,n+1,L,R).sum[beg]);
		}
		else
		{
			scanf("%d",&L);
			cin>>c;
			Assis(L,Code(c));
		}
	}
	return 0;
}