自动搬运

查看原文

来自洛谷，原作者为

	_ctz Ádigie šos ök iroг.

搬运于2025-08-24 22:02:01，当前版本为作者最后更新于2019-10-12 14:28:19，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

安利blog

传送门

妈妈我能独立切「SDOI2018R2」的题啦！

虽然这个题不难

向下取整满足结合律（并不知道为啥~~asuldb说这很显然~~）。然后把那个鬼畜的条件拆开（懒得打向下取整了）：

$a_{x/2}+a_{x/2/2}+a_{x/2/2/2}+...\equiv 0 \pmod m$

如果连上边数列就会变成这个样子：

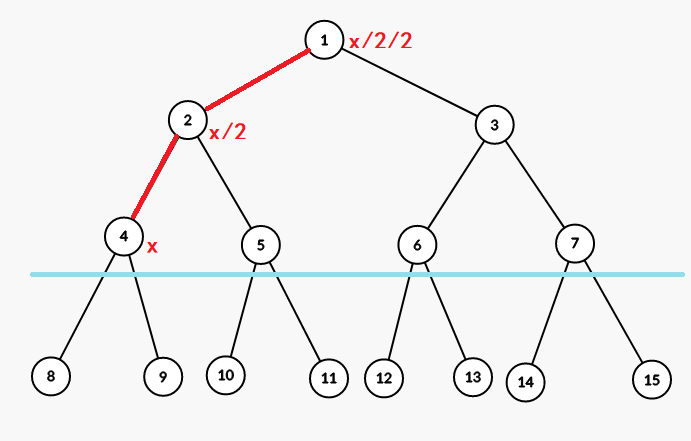
很明显构成了一棵完全二叉树。这个条件就能转化为从任意点出发，向下延伸包含$k+1$个点的路径权值和模$m$等于$0$。

再看上面那张图，令$k=2$，列两个式子：

$a_1+a_2+a_4\equiv 0\pmod m$

$a_2+a_4+a_8\equiv 0\pmod m$

$\therefore a_1\equiv a_8\pmod m$

同理，$a_1\equiv a_9\equiv a_{10}\equiv...a_{15}$，$a_2\equiv a_{16}\equiv a_{17}\equiv ... a_{23}\pmod m$

也就是说每个点与其子树内向下第$k+1$层的点最终的权值相等。

这样只要前$k+1$层的路径满足模$m$等于$0$，下面的所有路径就都满足。$DP$的时候要考虑的点数直接降到$2^{k+1}$个。

设$f(i,j)$为点$i$向下延伸至$k+1$层路径权值和模$m$为$j$的最小花费。

$O(n+m^22^{k+1})$预处理一个$v(i,j)$表示将点$i$以及与它相等的点权值全部改为$j$的花费。

直接枚举左右儿子的路径权值转移：

$f(i,j)=\min\{f(i<<1,k)+f(i<<1|1,k)+v(i,(j-k+m)\%m)\}$

从$2^{k+1}$开始倒着$DP$，答案就是$f(1,0)$。复杂度$O(Tn+Tm^22^{k+1})$。

代码：

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cmath>
#include <cstring>

#define maxn 10000005
#define inf 0x3f3f3f3f

using namespace std;

inline int read(){
	int x=0,y=0;
	char ch=getchar();
	while(ch<'0'||ch>'9'){if(ch=='-')y=1;ch=getchar();}
	while(ch>='0'&&ch<='9')x=(x<<1)+(x<<3)+(ch^48),ch=getchar();
	return y?-x:x;
}
int n,m,k,a[maxn],b[maxn],id[maxn];
long long f[1<<11][200],v[1<<11][200],tax[1<<11][200];
namespace file{
	unsigned int SA, SB, SC;
	int p, A, B;
	unsigned int rng61(){
		SA ^= SA << 16;
		SA ^= SA >> 5;
		SA ^= SA << 1;
		unsigned int t = SA;
		SA = SB;
		SB = SC;
		SC ^= t ^ SA;
		return SC;
	}
	void gen(){
		n=read(),k=read()+1,m=read(),p=read(),SA=read<unsigned>(),SB=read<unsigned>(),SC=read<unsigned>(),A=read(),B=read();
		for(int i = 1; i <= p; i++)a[i]=read()%m,b[i]=read();
		for(int i = p + 1; i <= n; i++){
			a[i] = (rng61() % A + 1)%m;
			b[i] = rng61() % B + 1;
		}
	}
}
int main(){
	int t=read();
	while(t--){
		file::gen();
		memset(v,0,sizeof v);
		memset(tax,0,sizeof tax);
		memset(f,0x3f,sizeof f);
		for(register int i=1;i<1<<k;++i)tax[id[i]=i][a[i]]=b[i];
		for(register int i=1<<k;i<=n;++i)tax[id[i]=id[i/(1<<k)]][a[i]]+=b[i];
		for(register int i=1;i<1<<k;++i){
			for(register int j=0;j<m;++j){
				for(register int k=0;k<j;++k)
					v[i][j]+=tax[i][k]*(j-k);
				for(register int k=j+1;k<m;++k)
					v[i][j]+=tax[i][k]*(j+m-k);
			}
		}
		for(register int i=1<<k-1;i<1<<k;++i)
			for(register int j=0;j<m;++j)
				f[i][j]=v[i][j];
		for(register int i=(1<<k-1)-1;i;--i)
			for(register int j=0;j<m;++j)
				for(register int k=0;k<m;++k)
					f[i][j]=min(f[i][j],f[i<<1][k]+f[i<<1|1][k]+v[i][(j-k+m)%m]);
		printf("%lld\n",f[1][0]);
		for(register int i=1;i<=n;++i)a[i]=b[i]=0;
	}
}