自动搬运

查看原文

来自洛谷，原作者为

	羽儇 自分で選んだ道は、たとえひざまずいても歩き終えます。

搬运于2025-08-24 22:01:56，当前版本为作者最后更新于2019-11-10 15:03:02，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

$P4612$

---

这题$AC$率挺高的说，窝$wa$了一次，为组织蒙羞（所用人交19，AC15）

那么$Solution:$

---

$I$存储

可以观察到，$Mirko$的朋友可以接到$Mirko$的范围是一个矩形,如：

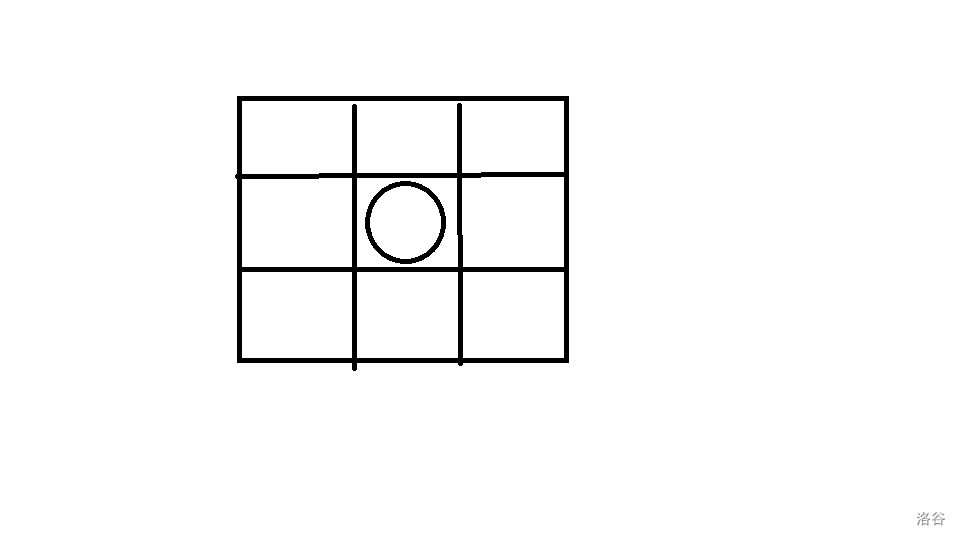
那么以便方便我们就用结构体来存

struct node 
{
	int ux,dx,ly,ry;
}a[400100];

$ux$指矩形上边，$dx$指矩形下边，$ly$矩形左边，$ry$矩形右边（待会要考的

---

$II$转移范围

我们可以发现，$Mirko$的出发点一定是在第一个朋友可以接到的范围内（不一定是在边缘上，即$t = a[1]$

可以记$t$为$Mirko$可以待的范围，从曾经范围内的点走相同的最短步数$d$而得来，如图

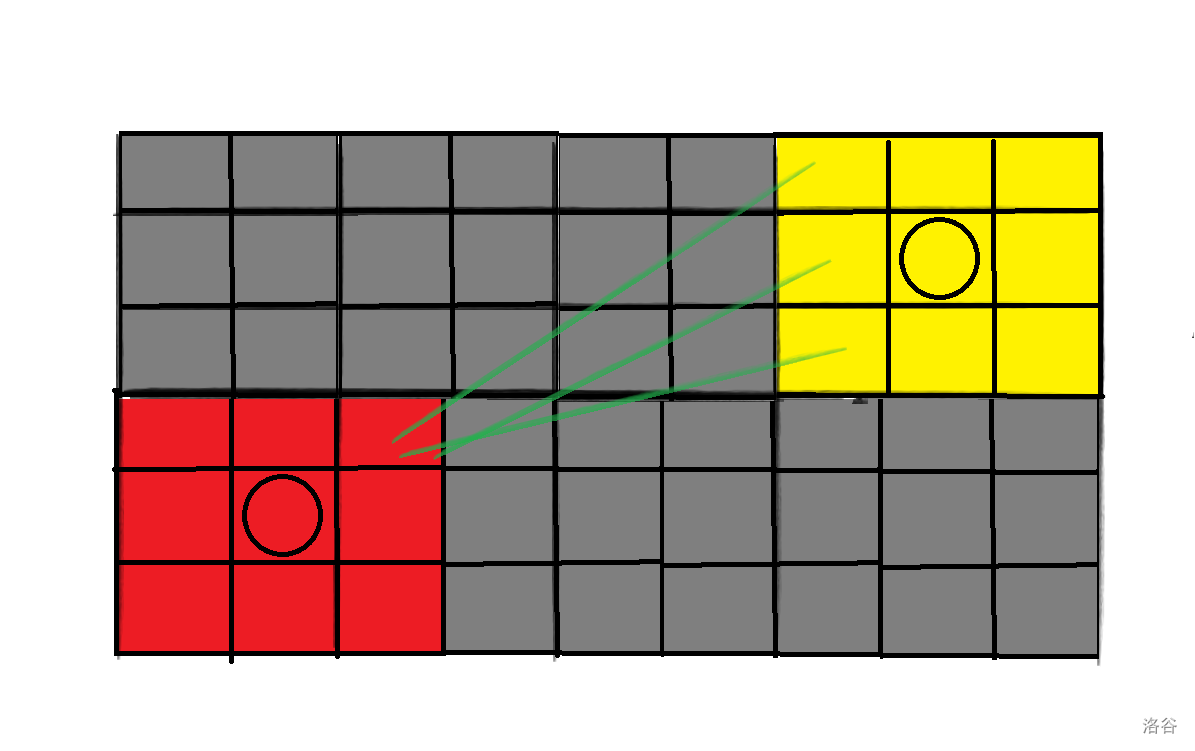
假设红色的范围是曾经可以待的范围（因为有时候保证最优的不止一个点），

那么每次更新出一个新的范围

而这个范围一定是个矩形，那么之后就说矩形吧（记几$yy$一下

---

$III$如何转移矩形

可以观察出，从当前所在的矩形$t$要转移到$a[i](i >= 2)$

共有两种可能：

$1$、 $t$ 与 $a[i]$　有交集，那么就一定不需要走，d = 0

然后把t更新为交集

交集求法

node Get_(node a1,node a2)
{
	node b = (node){min(a1.ux,a2.ux),max(a1.dx,a2.dx),max(a1.ly,a2.ly),min(a1.ry,a2.ry)};
	if(b.ux < b.dx || b.ly > b.ry)return (node){-1,-1,-1,-1};
	return b;
}

如果无交集，就更新为$-1$，以便于接下来判断

$2$、$t$ 与 $a[i]$ 无交集，那么需要走 d = max(max(a[i].dx-t.ux,t.dx-a[i].ux),max(a[i].ly-t.ry,t.ly-a[i].ry));

$a$.内部第一个$max$：一个矩形$a$的下底减去另一个矩形$b$的上底（反着再来一次

（解释一下内部$max$：我们要求的是距离最近的$a$与$b$的边的距离

即，竖着走的最小步数（没错，就是最小，自己借助下图$yy$

$b$.内部第二个$max$：一个矩形的左边减去另一个矩形的右边，即，横着走的最小步数

$c$.外部$max$：因为在斜着走的时候可以分成走两步，譬如，左上 = 左走$1$+上走$1$

那么横竖两方向走的少的就可以被抵消，最小步数就是大的那个

呃，不好理解呢，画个图吧

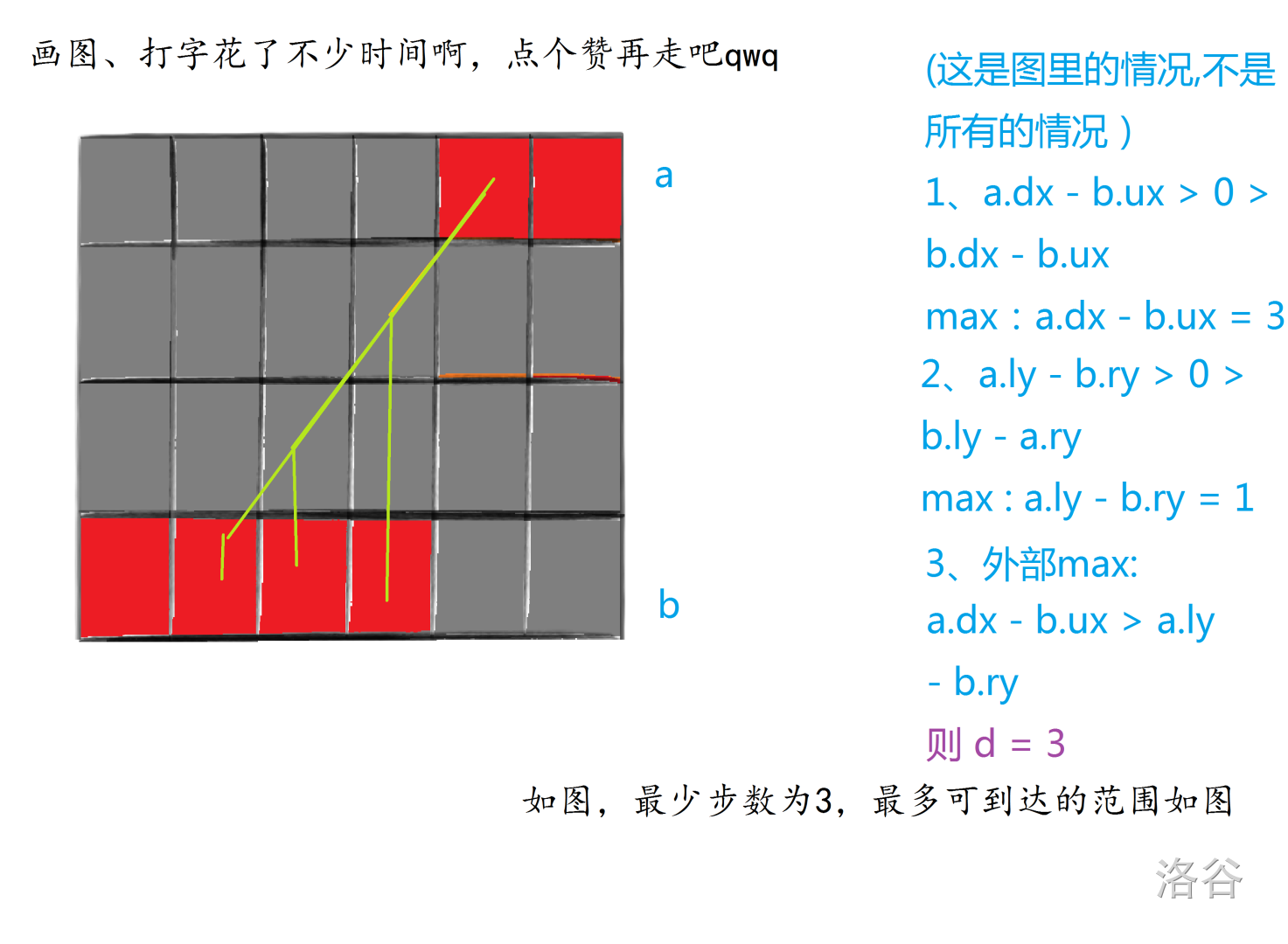
最后

t = Get_((node){t.ux+d,t.dx-d,t.ly-d,t.ry+d},a[i]);ans += (long long )d;

$t$往外扩张$d$ 与$a[i]$求交集。

---

$ACcode$

#include <cstdio>
#include <algorithm>
using namespace std;
int N,x,y,p;
struct node 
{
	int ux,dx,ly,ry;
}a[400100]; 
node Get_(node a1,node a2)
{
	node b = (node){min(a1.ux,a2.ux),max(a1.dx,a2.dx),max(a1.ly,a2.ly),min(a1.ry,a2.ry)};
	if(b.ux < b.dx || b.ly > b.ry)return (node){-1,-1,-1,-1};
	return b;
}
int main()
{
	scanf("%d",&N);
	for(int i = 1 ; i <= N ; i ++ )
	{
		scanf("%d%d%d",&x,&y,&p);
		a[i] = (node){x + p,x - p,y - p,y + p};
	}
	node t = a[1];long long ans = 0;
	for(int i = 2 ; i <= N ; i ++ )
	{
		node b = Get_(a[i],t);
		if(b.dx != - 1){t = b;continue;}
		int d = max(max(a[i].dx-t.ux,t.dx-a[i].ux),max(a[i].ly-t.ry,t.ly-a[i].ry));
		t = Get_((node){t.ux+d,t.dx-d,t.ly-d,t.ry+d},a[i]);ans += (long long )d;
	}
	printf("%lld",ans);
	return 0;
}

---

其实还可以在化简下

首先结构体变量有两个即可（节能主义万岁！$!$!

$l$ 相当于$t$，$now$为当前矩形

每次更新下 l

经过计算可以发现

在求交集时，如果相交，那么

d = max(max(now.dx-l.ux,l.dx-now.ux),max(now.ly-l.ry,l.ly-now.ry))

一定$<0$

那么我们使$d = 0$,反正原来如果有交集，$ans$也什么都不加

最后更新下$t$

#include <cstdio>
#include <algorithm>
using namespace std;
int N,x,y,p;
struct node 
{
	int ux,dx,ly,ry;
}l,now; 
int main()
{
	scanf("%d",&N);scanf("%d%d%d",&x,&y,&p);
	l = (node){x + p,x - p,y - p,y + p};
	long long ans = 0;
	for(int i = 2 ; i <= N ; i ++ )
	{
		scanf("%d%d%d",&x,&y,&p);
	    now = (node){x + p,x - p,y - p,y + p};
	    int d = max(max(now.dx-l.ux,l.dx-now.ux),max(now.ly-l.ry,l.ly-now.ry));
	    if(d < 0)d = 0;
	    ans += (long long)d;
	    l.dx = max(l.dx - d,now.dx);
	    l.ux = min(l.ux + d,now.ux);
	    l.ly = max(l.ly - d,now.ly);
	    l.ry = min(l.ry + d,now.ry);
	}
	printf("%lld",ans);
	return 0;
}