自动搬运

查看原文

来自洛谷，原作者为

	Conan15 天地正气，浩然长存，煌煌天威，以剑引之！

搬运于2025-08-24 22:01:39，当前版本为作者最后更新于2022-09-17 18:26:35，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

目录：

1. 前置知识
2. 前置知识讲解
3. 最小圆覆盖的最“玄学”之处
4. 讲解本题
5. 旋转坐标系
6. 优化
7. 时间复杂度分析

前置知识

最小圆覆盖。

前置知识讲解

会做这题其实对本题有帮助。 这题其实可以用几何算法以及模拟退火来做。

不过模拟退火相对来讲会很复杂，需要调很多参数……比如初始温度、降温系数等，很麻烦。

因此我们采用 几何算法 解决这道题目！！！

来看一下我解决“最小圆覆盖”的思路：

---

当 $n=1$ 的时候，最小圆覆盖当然圆心是第一个点 $p_1$，半径为 $0$。

当 $n=2$ 的时候，最小圆覆盖就是 “两点定圆” ，圆心是 $p_1p_2$ 线段的中心，半径是线段长度的一半。

当 $n=3$ 的时候，最小圆覆盖就复杂点了。分为两种情况：

1. $p_3$ 在上一个圆的圆周上或圆内。这种情况不会影响最小圆覆盖，忽略这个点。

2. $p_3$ 在上一个最小圆覆盖圆之外。这个时候 $p_3$ 一定在前三个点的最小圆覆盖的圆周上，才能满足“最小”的性质。那么现在原问题转化为子问题：从 $p_1p_2$ 中找出一或两个点，与点 $p_3$ 两点定圆或三点定圆。

当 $n=4$ 的时候，与 $n=3$ 的时候同理，分为两种情况，第一种直接忽略这个点，第二种则是从前面的点中挑出一或两个与 $p_4$ 一起定圆。

最后把所有的点都加入之后，就可以得出最小圆覆盖。

但是我们分析一下，会发现：需要一层循环枚举所有的点进行加入，一层循环来枚举两点定圆，还需要一层循环来枚举第三个点定圆……所以这个算法的时间复杂度是 $O(n^3)$ 的！

因为题目中，对于 $100\%$ 的数据，$1\leq N\leq 10^5$，$|x_i|,|y_i|\leq 10^4$。

在这个题目的数据范围下，显然是过不了的！

最小圆覆盖的最“玄学”之处

解决这个问题，需要在求解之前，用 STL 函数 random_shuffle() 打乱这些点。

这题的玄学之处就是在于此，在随机情况下它的效率期望是线性的。

可以结合代码理解一下。

#include <bits/stdc++.h>

using namespace std;

#define eps 1e-8

const int N = 500010;

int sgn(double x) {
    if (fabs(x) < eps) return 0;
    if (x < 0) return -1;
    return 1;
}

struct Point {
    double x, y;
};

double Distance(Point A, Point B) {
    return hypot(A.x - B.x, A.y - B.y);
}

Point circle_center(const Point a, const Point b, const Point c) {
    Point center;
    double a1 = b.x - a.x, b1 = b.y - a.y, c1 = (a1 * a1 + b1 * b1) / 2;
    double a2 = c.x - a.x, b2 = c.y - a.y, c2 = (a2 * a2 + b2 * b2) / 2;
    double d = a1 * b2 - a2 * b1;
    center.x = a.x + (c1 * b2 - c2 * b1) / d;
    center.y = a.y + (a1 * c2 - a2 * c1) / d;
    return center;
}

void min_cover_circle(Point * p, int n, Point &c, double &r) {
    random_shuffle(p + 1, p + 1 + n);
    c = p[1]; r = 0;
    for (int i = 2; i <= n; i++) {
        if (sgn(Distance(p[i], c) - r) > 0) {
            c = p[i]; r = 0;
            for (int j = 1; j < i; j++)
                if (sgn(Distance(p[j], c) - r) > 0) {
                    c.x = (p[i].x + p[j].x) / 2;
                    c.y = (p[i].y + p[j].y) / 2;
                    r = Distance(p[j], c);
                    for (int k = 1; k < j; k++)
                        if (sgn(Distance(p[k], c) - r) > 0) {
                            c = circle_center(p[i], p[j], p[k]);
                            r = Distance(p[i], c);
                        }
                }
        }
    }
}

int main() {
    int n; Point p[N], c; double r;
    while (~scanf("%d", &n) && n) {
        for (int i = 1; i <= n; i++) scanf("%lf%lf", &p[i].x, &p[i].y);
        min_cover_circle(p, n, c, r);
        printf("%.10lf\n%.10lf %.10lf", r, c.x, c.y);
    }
    return 0;
}

以上的讲解只是为了让读者更清楚思路，接下来看看这一题要怎么做。

讲解本题

题目的意思就是用两个相同大小的圆覆盖平面所有的点，求圆的最小半径，因此它称作最小覆盖双圆问题。

很显然的，既然要分成两个圆，那么一定是用一条直线分割成两个点集，然后分别求出两个点集的最小圆覆盖的半径 $r_1r_2$，答案就是 $\max(r1,r2)$。

要求出这条直线的位置，其实很容易地可以想到用二分。

旋转坐标系

这里所说的是：用二分求出一条与 $X$ 轴垂直的直线，然后再求解。

但是还有一种情况未考虑——如果正解是斜着画一条直线呢？

可以大胆地猜想：既然我们不能控制直线的角度，那我们就干脆把整个坐标系旋转！这个想法虽然有些疯狂，但是它其实是正解！

每次旋转之后都求一次最小双圆覆盖，然后再取最优值即是答案。问题就在于如何对每个点进行“旋转”?

为了保证题解的严谨，我上网搜了一张图片说明。

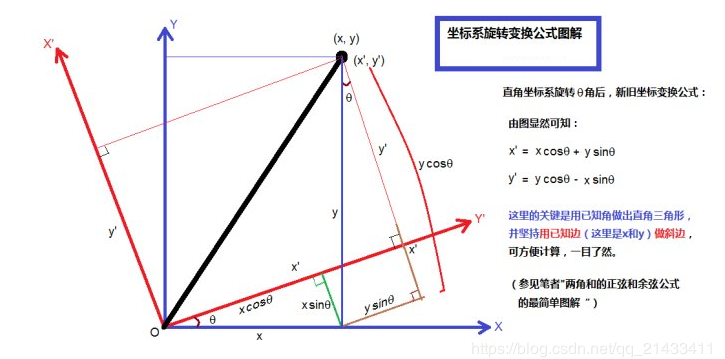
对于这个坐标系，只需要旋转 $180$ 度就可以了，因为把坐标系旋转 $180$ 度后就又回到了第一次计算的问题。

推导了这么多，对于“最小双圆覆盖”部分就能直接套上一题的模板，再加上一些额外的坐标系旋转、二分，这题就可以得到解决了。

优化

但是有一个很重要的优化：在二分的时候，如果当前的 $\min(r1,r2)$ 无法更新答案，则后面都无法更新答案，直接退出二分。

如果没有这个优化则之后 $60$ 分……亲测了，每次写代码都要注意优化。

时间复杂度分析

分析的同时顺便回顾一下思路，这里不会计算数据组数。

时间复杂度（有错请指出，谢谢）：

1. 每次需要枚举坐标系旋转的度数 $180$（常数大了点）。

2. 并且需要 $O(N)$ 对每个点改变位置。

3. 之后进行二分（$\log N$ 的效率），每次二分内需要做两次 $O(N)$ 的最小圆覆盖，所以二分的复杂度是 $O(N \log N)$ 的。

因此我分析出的总时间复杂度是：$O(180 \times N \log N)$。因为常数过大，我就把这个 $180$ 给扔进去了……

代码：

#include <bits/stdc++.h>

#define eps 1e-8
const double _ = 1.0 / 180 * acos(-1);
const double Cos = cos(_), Sin = sin(_);

using namespace std;

const int N = 1010;
double r;
struct Point {
    double x, y;
} c, a[N], p[N];

inline Point rotate(const Point &b) {
    Point t;
    t.x = b.x * Cos + b.y * Sin;
    t.y = b.y * Cos - b.x * Sin;
    return t;
}

inline int sgn(double x) {
    if (fabs(x) < eps) return 0;
    if (x < 0) return -1;
    return 1;
}

inline Point circle_center(const Point a, const Point b, const Point c) {
    Point center;
    double a1 = b.x - a.x, b1 = b.y - a.y, c1 = (a1 * a1 + b1 * b1) / 2;
    double a2 = c.x - a.x, b2 = c.y - a.y, c2 = (a2 * a2 + b2 * b2) / 2;
    double d = a1 * b2 - a2 * b1;
    center.x = a.x + (c1 * b2 - c2 * b1) / d;
    center.y = a.y + (a1 * c2 - a2 * c1) / d;
    return center;
}
inline double Dis(Point A, Point B) {
    return hypot(A.x - B.x, A.y - B.y);
}
inline double min_cover_circle(int L, int R) {
    if (L > R) return 0;
    for (int i = L; i <= R; i++) a[i] = p[i];

    random_shuffle(a + L, a + 1 + R);
    c = a[L]; r = 0;
    for (int i = L; i <= R; i++)
        if (sgn(Dis(a[i], c) - r) > 0) {
            c = a[i]; r = 0;
            for (int j = L; j < i; j++)
                if (sgn(Dis(a[j], c) - r) > 0) {
                    c.x = (a[i].x + a[j].x) / 2;
                    c.y = (a[i].y + a[j].y) / 2;
                    r = Dis(c, a[j]);
                    for (int k = L; k < j; k++)
                        if (sgn(Dis(a[k], c) - r) > 0) {
                            c = circle_center(a[i], a[j], a[k]);
                            r = Dis(a[k], c);
                        }
                }
        }
    return r;
}

inline int cmp(Point a, Point b) {
    return a.x < b.x;
}

int main() {
    int n;
    while (scanf("%d", &n), n) {
        double R = 1e9;
        for (int i = 1; i <= n; i++) scanf("%lf%lf", &p[i].x, &p[i].y);
        for (int i = 1; i <= 180; i++) {  //坐标系旋转枚举次数
            for (int i = 1; i <= n; i++) p[i] = rotate(p[i]);
            sort(p + 1, p + n + 1, cmp);
            int l = 1, r = n;
            while (l <= r) {
                int mid = (l + r) / 2;
                double R1 = min_cover_circle(1, mid), R2 = min_cover_circle(mid + 1, n);
                if (min(R1, R2) > R) break; //剪枝优化，不然会TLE
                if (R1 < R2) l = mid + 1;
                else r = mid - 1;
                R = min(R, max(R1, R2));
            }
        }
        printf("%.2f\n", R);
    }
    return 0;
}