自动搬运

查看原文

来自洛谷，原作者为

	liangbowen 不能再摆了，，，

搬运于2025-08-24 22:01:31，当前版本为作者最后更新于2022-10-05 11:38:05，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

前言

题目传送门！

更好的阅读体验？

双倍经验：P3554（数据坑一点）。简要题意可以看 P3554。

思路：二分答案 + 树形 DP。

思路

答案显然具有单调性，所以考虑二分答案。

$\operatorname{chk(k)}$ 判定这个 $k$ 是否能使 A 获胜。

容易想到贪心，但实际上并不可行。这是同机房巨佬的 hack。于是考虑 DP。

---

首先两人都很聪明，所以 B 会一直从根往下走；A 会一直在 B 下面的层染色。

最麻烦的是，在对一个子树染色时，可能会出现染不够的情况。但这并不意味着 $k$ 不成立，因为 $i$ 的祖先可能会有剩余的没有染色。

听起来非常难懂，举个例子，$k = 3$。

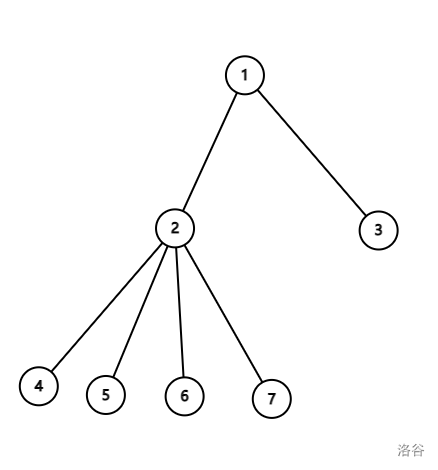
如果只看以 $2$ 为根的子树，显然无法染完。

但是如果看以 $1$ 为根的整棵树，发现：染完 $2,3$ 号点后还能再染一次，这样可以帮 $2$ 为根的子树染一下。于是 $k = 3$ 就成立了。

我们就可以用这个性质实现 DP。

---

设 $dp_i$ 表示以 $i$ 为根的子树，需要 $dp_i$ 次祖先的帮助。

那么就有转移方程（为了美观，分了两行）：

$$\texttt{sum} = \sum\limits_{\text{v : son of u}} dp_v + 1 $$$$dp_u = \max\{0, \texttt{sum} - k\}$$

$\texttt{sum}$ 即为子树需要的帮助次数。每次加 $(dp_v + 1)$，是因为还要染 $v$，所以加了一。

那么 $k$ 能成立，当且仅当 $dp_1 = 0$。

这题就愉快地做完啦！

完整代码

#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;
const int N = 3e5 + 5;
struct Edge {int now, nxt;} e[N << 1];
int head[N], cur;
void add(int u, int v)
{
	e[++cur].now = v;
	e[cur].nxt = head[u];
	head[u] = cur;
}
int k, dp[N];
void dfs(int u, int fa) //按照转移方程来就好了
{
	int sum = 0;
	for (int i = head[u]; i; i = e[i].nxt)
	{
		int v = e[i].now;
		if (v != fa) dfs(v, u), sum += dp[v] + 1; 
	}
	dp[u] = max(0, sum - k);
}
bool chk(int x)
{
	k = x, dfs(1, -114514);
	return !dp[1]; //等同于 return dp[1] == 0
}
int FIND(int l, int r) //二分答案
{
	while (l < r)
	{
		int mid = (l + r) >> 1;
		if (chk(mid)) r = mid;
		else l = mid + 1;
	}
	return r;
}
int main()
{
    ios::sync_with_stdio(false);
	int n;
	cin >> n;
	for (int i = 1; i < n; i++)
	{
		int u, v;
		cin >> u >> v;
		add(u, v), add(v, u);
	}
	cout << FIND(0, n); //注意 l=0，否则 n=1 会叉掉
    return 0;
}

希望能帮助到大家！